初三下学期期中数学考试题
一、 选择题:(本题共78分,每小题3分)
在下列各题的四个备选答案中,只有一个是正确的。
1. ![]() 的相反数是( )
的相反数是( )
A. ![]() B.
B.
![]() C.
3 D.
C.
3 D.
![]()
2. 计算![]() 的结果是( )
的结果是( )
A. 0 B. 1 C. ![]() D.
D.
![]()
3. 若![]() ,则
,则![]() 的补角为( )
的补角为( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
4. 羊年话“羊”,“羊”字象征着美好和吉祥,下列图案都与“羊”字有关,其中是轴对称图形的个数是( )

A. 1 B. 2 C. 3 D. 4
5. 函数![]() 的自变量x的取值范围是( )
的自变量x的取值范围是( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
6. 2003年5月19日,国家邮政局特别发行“万众一心 抗击‘非典’”邮票,收入全部捐赠给卫生部门,用以支持抗击“非典”斗争,其邮票发行量为枚,用科学记数法表示正确的是( )
A. ![]() 枚 B.
枚 B.
![]() 枚
枚
C. ![]() 枚 D.
枚 D.
![]() 枚
枚
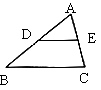
7. 如图,在![]() 中,D、E分别是AB、AC边上的中点,若DE=4,则BC等于( )
中,D、E分别是AB、AC边上的中点,若DE=4,则BC等于( )
A. 2 B. 4 C. 8 D. 12
8. 用换元法解方程![]() ,设
,设![]() ,则原方程可化为( )
,则原方程可化为( )
A. ![]() B.
B.
![]()
C. ![]() D.
D.
![]()
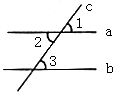
9. 如图,直线c与直线a、b相交,且a//b,则下列结论:(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 中正确的个数为( )
中正确的个数为( )
A. 0 B. 1 C. 2 D. 3
10. 点![]() 关于x轴对称的点的坐标为( )
关于x轴对称的点的坐标为( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
11. 下列各式中正确的是( )
A. ![]() B.
B.
![]()
C. ![]() D.
D.
![]()
12. 若两圆相交,则这两圆的公切线( )
A. 只有一条 B. 有两条 C. 有三条 D. 有四条
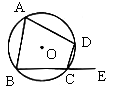
13. 如图,四边形ABCD内接于⊙O,E在BC延长线上,若![]() ,则
,则![]() 等于( )
等于( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
14. 不等式组![]() 的解集是( )
的解集是( )
A. ![]() B.
B.
![]()
C. ![]() D.
D.
![]() 或
或![]()
15. 在下列二次根式中与![]() 是同类二次根式的是( )
是同类二次根式的是( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
16. 在![]() 中,
中,![]() ,则cosA等于( )
,则cosA等于( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
17. 方程![]() 根的情况是( )
根的情况是( )
A. 只有一个实数根 B. 有两个相等的实数根
C.有两个不相等的实数根 D. 没有实数根
18. 已知反比例函数![]() 的图象经过点(1,2),则函数
的图象经过点(1,2),则函数![]() 可确定为( )
可确定为( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
19. 如图,在方格纸中有四个图形<1>、<2>、<3>、<4>,其中面积相等的图形是( )
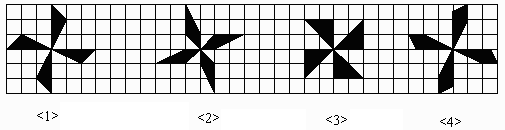
A. <1>和<2> B. <2>和<3> C. <2>和<4> D. <1>和<4>
20. 若![]() ,则xy的值等于( )
,则xy的值等于( )
A. ![]() B.
B.
![]() C.
2 D.
6
C.
2 D.
6
21. 如果圆柱的母线长为5cm,底面半径为2cm,那么这个圆柱的侧面积是( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
22. 二次函数![]() 的图象如图所示,则下列结论正确的是( )
的图象如图所示,则下列结论正确的是( )
A. ![]() B.
B.
![]()
C. ![]() D.
D.
![]()
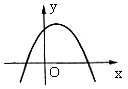
23. 如图,PA切⊙O于点A,PO交⊙O于点B,若PA=6,BP=4,则⊙O的半径为( )
A. ![]() B.
B.
![]() C.
2 D.
5
C.
2 D.
5
24. 某同学在测量体温时意识到体温计的读数与水银柱的长度之间可能存在着某种函数关系,就此他与同学们选择了一种类型的体温计,经历了收集数据、分析数据、得出结论的探索过程,他们收集到的数据如下:
| 体温计的读数t(℃) | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 |
| 水银柱的长度l(mm) | 56.5 | 62.5 | 68.5 | 74.5 | 80.5 | 86.5 | 92.5 | 98.5 |
请你根据上述数据分析判断,水银柱的长度l(mm)与体温计的读数t(℃)(![]() )之间存在的函数关系是( )
)之间存在的函数关系是( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
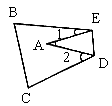
25. 如图,把![]() 纸片沿DE折叠,当点A落在四边形BCDE内部时,则
纸片沿DE折叠,当点A落在四边形BCDE内部时,则![]() 与
与![]() 之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是( )
之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是( )
A. ![]() B.
B.
![]()
C. ![]() D.
D.
![]()
26. 甲、乙两同学约定游泳比赛规则:甲先游自由泳到泳道中点后改为蛙泳,而乙则是先游蛙泳到泳道中点后改为自由泳,两人同时从泳道起点出发,最后两人同时游到泳道终点。又知甲游自由泳比乙游自由泳速度快,并且二人自由泳均比蛙泳速度快,若某人离开泳道起点的距离s与所用时间t的函数关系可用图象表示,则下列选项中正确的是( )
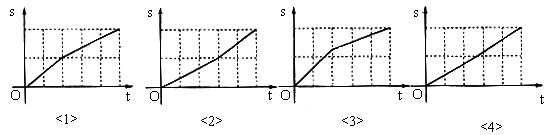
A. 甲是图<1>,乙是图<2> B. 甲是图<3>,乙是图<2>
C. 甲是图<1>,乙是图<4> D. 甲是图<3>,乙是图<4>
填空题:(本题共21分,每空3分)
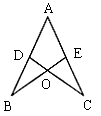
27. 如图,点D在AB上,点E在AC上,CD与BE相交于点O,且AD=AE,AB=AC,若![]() ,则
,则![]()
28. 分解因式:![]() _________
_________
29. 若三角形的两边长分别为6、7,则第三边长a的取值范围是_______
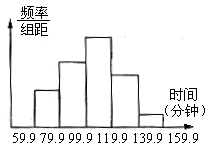
30. 今年5月海淀区教育网开通了网上教学,某校初三年级(8)班班主任为了了解学生上网学习时间,对本班40名学生某天上网学习时间进行了调查,将数据(取整数)整理后,绘制出如图所示频率分布直方图。已知从左至右各个小组的频率分别是0.15、0.25、0.35、0.20、0.05,则根据直方图所提供的信息,这一天上网学习时间在100~119分钟之间的学生人数是_________人。如果只用这40名学生这一天上网学习时间作为样本去推断该校初三年级全体学生该天上网学习时间,这样的推断是否合理?_______(填“合理”或“不合理”)
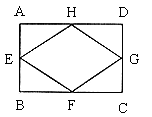
31. 如图,在矩形ABCD中,E、F、G、H分别为AB、BC、CD、DA的中点,若![]() ,四边形EFGH的周长为40cm,则矩形ABCD的面积为_______
,四边形EFGH的周长为40cm,则矩形ABCD的面积为_______![]() 。
。
32. 已知二次函数![]() 与x轴交点的横坐标为
与x轴交点的横坐标为![]() ,则对于下列结论:<1>当
,则对于下列结论:<1>当![]() 时,
时,![]() ;<2>当
;<2>当![]() 时,
时,![]() ;<3>方程
;<3>方程![]() 有两个不相等的实数根
有两个不相等的实数根![]() ;<4>
;<4>![]() ;<5>
;<5>![]() ,其中所有正确的结论是________(只需填写序号)
,其中所有正确的结论是________(只需填写序号)
解答题:(本题共21分,第33题5分,第34题7分,第35题9分)
33. 某同学在A、B两家超市发现他看中的随身听的单价相同,书包单价也相同,随身听和书包单价之和是452元,且随身听的单价比书包单价的4倍少8元。
(1)求该同学看中的随身听和书包单价各是多少元?
(2)某一天该同学上街,恰好赶上商家促销,超市A所有商品打八折销售,超市B全场购物满100元返购物券30元销售(不足100元不返券,购物券全场通用),但他只带了400元钱,如果他只在一家超市购买看中的这两样物品,你能说明他可以选择哪一家购买吗?若两家都可以选择,在哪一家购买更省钱?
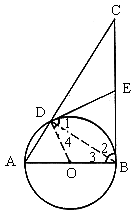
34. 已知:以![]() 的直角边AB为直径作⊙O,与斜边AC交于点D,E为BC边上的中点,连结DE。
的直角边AB为直径作⊙O,与斜边AC交于点D,E为BC边上的中点,连结DE。
(1)如图,求证:DE是⊙O的切线;
(2)连结OE,AE,当![]() 为何值时,四边形AOED是平行四边形,并在此条件下求
为何值时,四边形AOED是平行四边形,并在此条件下求![]() 的值。
的值。
(第(2)问答题要求:不要求写出解题过程,只需将结果填写在答题卡相应题号的横线上。)
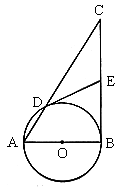
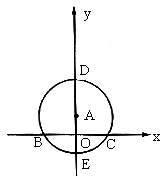
35. 已知:如图,点A在y轴上,⊙A与x轴交于B、C两点,与y轴交于点D(0,3)和点![]()
(1)求经过B、E、C三点的二次函数的解析式;
(2)若经过第一、二、三象限的一动直线切⊙A于点P(s,t),与x轴交于点M,连结PA并延长与⊙A交于点Q,设Q点的纵坐标为y,求y关于t的函数关系式,并观察图形写出自变量t的取值范围;
(3)在(2)的条件下,当y=0时,求切线PM的解析式,并借助函数图象,求出(1)中抛物线在切线PM下方的点的横坐标x的取值范围。
【参考答案】
选择题:(本题共78分,每小题3分)
1. C 2. B 3. D 4. B 5. A
6. C 7. C 8. A 9. D 10. D
11. C 12. B 13. B 14. C 15. A
16. A 17. D 18. A 19. A 20. A
21. D 22. D 23. B 24. C 25. B
26. C
填空题:(本题共21分,每空3分)
27. 20 28.
![]()
29. ![]() 30.
14,不合理
30.
14,不合理
31. 192 32. <1><3><4>
解答题:(本题共21分,第33题5分,第34题7分,第35题9分)
33. 解:(1)解法一:设书包的单价为x元,则随身听的单价为![]() 元
元
根据题意,得![]() ……1分
……1分
解这个方程,得
![]()
![]()
答:该同学看中的随身听单价为360元,书包单价为92元。 ……2分
解法二:设书包的单价为x元,随身听的单价为y元
根据题意,得![]() ……1分
……1分
解这个方程组,得![]()
答:该同学看中的随身听单价为360元,书包单价为92元。 ……2分
(2)在超市A购买随身听与书包各一件需花费现金:
![]() (元)
(元)
因为![]() ,所以可以选择超市A购买。 ……3分
,所以可以选择超市A购买。 ……3分
在超市B可先花费现金360元购买随身听,再利用得到的90元返券,加上2元现金购买书包,总计共花费现金:
![]() (元)
(元)
因为![]() ,所以也可以选择在超市B购买。 ……4分
,所以也可以选择在超市B购买。 ……4分
因为![]() ,所以在超市A购买更省钱。 ……5分
,所以在超市A购买更省钱。 ……5分
34. (1)证法一:连结OD、DB
![]() AB是⊙O的直径
AB是⊙O的直径
![]()
![]()
![]() E为BC边上的中点
E为BC边上的中点
![]()
![]() ……1分
……1分
![]()
![]()
![]() ……2分
……2分
![]() 在
在![]() 中,
中,![]()
![]()
![]() D为⊙O上的点
D为⊙O上的点
![]() DE是⊙O的切线 ……3分
DE是⊙O的切线 ……3分
证法二:连结OD、OE
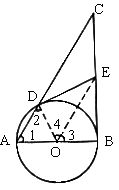
![]()
![]() E为BC边上的中点,O为AB边上的中点
E为BC边上的中点,O为AB边上的中点
![]()
![]()
![]() ……1分
……1分
![]()
![]()
![]() ……2分
……2分
![]() 为直角三角形
为直角三角形
![]()
![]() D为⊙O上的点
D为⊙O上的点
![]() DE是⊙O的切线 ……3分
DE是⊙O的切线 ……3分
(2)解:![]() ……4分
……4分
![]() ……7分
……7分
35. 解:(1)解法一:连结AC
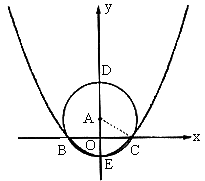
![]() DE为⊙A的直径,
DE为⊙A的直径,![]()
![]()
![]()
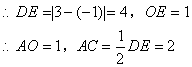
在![]() 中,
中,![]()
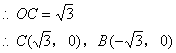
设经过B、E、C三点的抛物线的解析式为![]() ,则
,则
![]()
解得![]()
![]() ……2分
……2分
解法二:![]() DE为⊙A的直径,
DE为⊙A的直径,![]()
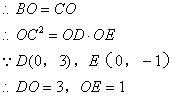
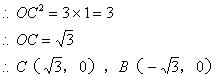
以下同解法一
(2)解法一:过点P作![]() 轴于F,过点Q作
轴于F,过点Q作![]() 轴于N
轴于N
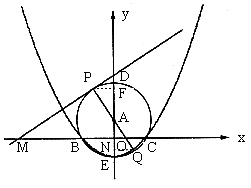
![]() ,F点的纵坐标为t
,F点的纵坐标为t
N点的纵坐标为y

![]() 动切线PM经过第一、二、三象限
动切线PM经过第一、二、三象限
观察图形可得![]()
![]()
即![]()
![]() 关于t的函数关系式为
关于t的函数关系式为![]() ……5分
……5分
解法二:(i)当经过一、二、三象限的切线PM运动到使得Q点与C点重合时,![]()
连结PB
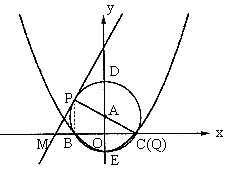
![]() PC是直径
PC是直径 ![]()
![]() 轴
轴 ![]()
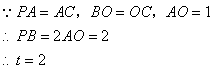
即![]() 时,
时,![]()
(ii)当经过一、二、三象限的切线
PM运动使得Q点在x轴上方时,![]()
观察图形可得![]()
过P作![]() 轴于S,过Q作
轴于S,过Q作![]() 轴于T
轴于T
则PS//AO//QT
![]() 点A为线段PQ的中点
点A为线段PQ的中点
![]() 点O为线段ST的中点
点O为线段ST的中点
![]() AO为梯形QTSP的中位线
AO为梯形QTSP的中位线
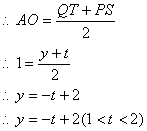
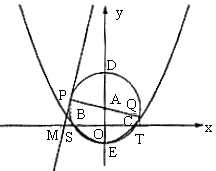
(iii)当经过一、二、三象限的切线PM运动使得Q点在x轴下方时,![]() ,观察图形可得
,观察图形可得![]()
过![]() 作
作![]() 轴于S,过Q作
轴于S,过Q作![]() 轴于T,设PQ交x轴于R
轴于T,设PQ交x轴于R
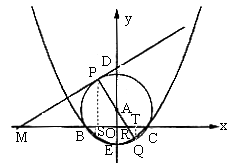
则QT//PS
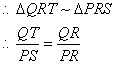
设![]() ,则
,则![]()
又![]() 轴,
轴,![]()
![]()
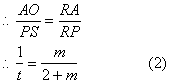
由(1)、(2)得![]()
![]()
综上所述:y与t的函数关系式为![]() ……5分
……5分
(3)解法一:当![]() 时,Q点与C点重合,连结PB
时,Q点与C点重合,连结PB
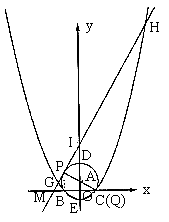
![]() PC为⊙A的直径
PC为⊙A的直径
![]()
即![]() 轴
轴
![]()
将![]() 代入
代入![]() ,得
,得![]()
![]()
![]()
设切线PM与y轴交于点I,则![]()
![]()
在![]() 与
与![]() 中
中
![]()
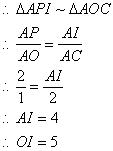
![]() I点坐标为(0,5)
I点坐标为(0,5)
设切线PM的解析式为![]()
![]() P点的坐标为
P点的坐标为![]()
![]()
解得![]()
![]() 切线PM的解析式为
切线PM的解析式为![]() ……7分
……7分
设切线PM与抛物线![]() 交于G、H两点
交于G、H两点
由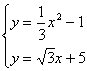 可得
可得
![]()
因此,G、H的横坐标分别为![]()
根据图象可得抛物线在切线PM下方的点的横坐标x的取值范围是
![]() ……9分
……9分
解法二:同(3)解法一
可得![]()
![]() 直线PM为⊙A的切线,PC为⊙A的直径
直线PM为⊙A的切线,PC为⊙A的直径
![]()
在![]() 与
与![]() 中
中
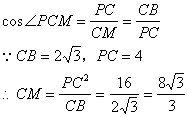
设M点的坐标为(m,0)
则![]()
![]()
即![]()
设切线PM的解析式为![]() ,得
,得
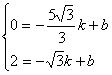
解得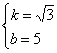
![]() 切线PM的解析式为
切线PM的解析式为![]() ……7分
……7分
以下同解法一。