一．实数与代数式

1．应用性问题

小楼家有祖父母，父母和他自己4口人，已知父母年龄之和为，母和小楼年龄之和为岁，父和小楼年龄之和为岁，祖母年龄比父、母、小楼年龄总和小5岁，那么祖母年龄为＿＿＿岁。（答案：）

2．探索性问题

在同一平面内二条直线相交有一个交点，两两相交的3条直线有3个交点，那么两两相交的4条直线有＿＿＿交点，两两相交的5条直线有＿＿＿＿个交点，试猜想两两相交的几条直线有＿＿＿＿个交点。（答案：6，10，。）

3．开放性问题：

尽可能多的写出－3和3之间的无理数。答案略。

二．函数、方程（组）和不等式（组）

1．应用性问题

有四种原料：（1）50％的酒精溶液150克；（2）90％的酒精溶液45克；

（3）纯酒精45克；　（4）水45克，请你设计一种方案，只选取三原料。

（各取若干或全部）配制成60％的酒精溶液200克。

①　  你选取哪三种原料，各取多少？

②设未知数，列方程（组）并解之，说明你配制方法的正确。

（答案：①可取50％的酒精溶液150克，纯酒精45克，水5克。②略）

2．探索性问题

已知1＋3＝4＝2²

1＋3＋5＝9＝3²

根据上面各式的规律，可以知道：当为正整数时1＋3＋5＋7…＋　

　的结果为＿＿＿＿＿＿。（答案：）

3．开放性问题

试设计一个应用题，使其满足如下方程组的形式。

　

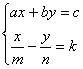
三．三角形和四边形

1．应用性问题

如图，园林部门准备在三条公路围成的地块内建造一个圆形的花坛，要求花坛面积尽量大，那么花坛应如何设计：（现测出AB＝34米，BC＝20米，CA＝42米）

2．探索性问题

直角梯形ABCD中，AD∥BC，∠A＝∠B＝90⁰

（1）试猜想：AD，BC，CD之间满足什么条件时，在CD上仅能找到一个点P使得AP⊥BP？（2）猜想AD，BC，CD之间满足什么条件时能找到两个点P，使AP⊥BP？（3）何时不存在这样的点P呢？（答案：（1）当AD＋BC＝CD时，可以通过以AB为直线作半圆与CO的交点个数来确定直角个数。（2）AD＋BC＜CD（3）AD＋BC＞CD＝

3．开放性问题

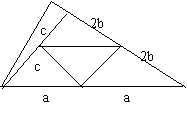
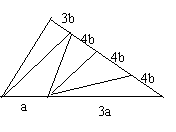
试用几种不同的方案将△ABC或面积相等的五个部分，并指出面积相等的是哪五部分（只在图上保留分割痕迹和必要的标注，不写作法）

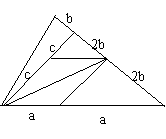
答案：

b

四．相似三角形

1．应用性问题

A，B两地的路程为20KM，甲、乙两人分别步行和骑车从A到B，乙晚1小时到达而早20分钟到达，解议程S和时间的函数，如图所示，则甲、乙相遇处B还有＿＿＿KM。

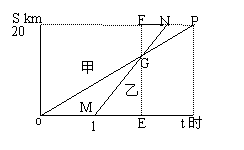答案：如图标上字母

由△GNP∽△OMG可得到，

又因OM＝1，NP＝，故，故FG＝

2．探索性问题

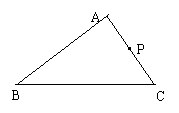
如图，在三角形ABC中，AB＝9，AC＝12，BC＝18，D是AC的中点，在AB上取一点E，连结DE，如果以A，D，E为顶点的三角形与三角形ABC相似，那么DE＝＿＿＿＿＿＿。

3．开放性问题

试尽可能多的设计分法，将Rt△分割成四个小三角形，使得每个小三角形与原三角形都相似。

五．其他

1．四边形通过一个顶点可以引一条对角线，五边形通过一个顶点可以引2条对角线，六边形通过同一个顶点可以引＿＿＿＿条对角线边形通过同一个顶点可以引＿＿＿＿条对角线，试猜想边形总共有＿＿＿＿条对角线。（答案： 3，

2．如图AB表示30米高的大楼，BC表示安装在大楼顶部的广告牌BC＝6米，A．B．C在同一直线上，AD表示地面，S表示人在地面上的位置（现在还未标出）当∠BSC最大时，人看广告牌的视角最大，即观看最清晰，试确定点S，使此人观看广告牌最清晰，并求出AS的长。

（答案：可以画出经B，C且与AD相切的圆弧，切点为S，AS＝（米））

3．为使二次三项式可以因式分解（在整数范围内）P可以取哪些整数？为了使式子可以因工分解（在整数范围内）尽可能多地找出适合的值！（略）

4．现有树9棵，把它们栽成三行，要求每行恰好为4棵，试尽可能多的找出符合题意的方法。（答案略）