2006年浙江省基础教育课程改革实验区初中学业水平考试调研
数学参考答案及评分意见
一、选择题(本题有5个小题,每小题4分,共20分)
| 题号 | 1 | 2 | 3 | 4 | 5 |
| 答案 | C | A | A | D | B |
二、填空题(本题有3个小题,每小题5分,共15分)
6. ![]() .
.
7. ①②(注:本题是开放题,答案不唯一,只要正确就给分).
8.
(1)![]() (5分) (2)
(5分) (2)![]() [第(1)题不答,第(1)题正确3分]
[第(1)题不答,第(1)题正确3分]
三、解答题(本题有4小题,共40分)
9.(本题8分)
解:由![]() ,解得
,解得![]() .································································· 3分
.································································· 3分
由![]() ,解得
,解得![]() .····························································· 3分
.····························································· 3分
∴
不等式组的解是![]() .·························································· 2分
.·························································· 2分
 10.(本题8分)
10.(本题8分)
解:由于A1,A2 ,A3 在直线![]() 上,且四边形A1 B1
C1 O,A2 B2 C2C1, A3 B3
C3C2均为正方形,
上,且四边形A1 B1
C1 O,A2 B2 C2C1, A3 B3
C3C2均为正方形,
∴ A1(0,1) , C1(1,0).······· 2分
A2(1,![]() ).·································· 2分
).·································· 2分
C2(![]() ,0),A3(
,0),A3(![]() ,
,![]() ).································································ 2分
).································································ 2分
C3(![]() ,0),B3(
,0),B3(![]() ,
,![]() ).····························································· 2分
).····························································· 2分
11.(本题12分)
 解:(1)∵菱形ABGH、BCFG、CDEF全等,
解:(1)∵菱形ABGH、BCFG、CDEF全等,
∴ BC=CD=DE=6,AD=3AB=18.····· 2分
∵ BG∥DE,
∴ ∠ABP=∠D,∠APB=∠AED.
∴ △ABP∽△ADE.······················· 2分
∴ ![]() ,
,![]() .································ 2分
.································ 2分
(2)图中的ΔEGP与ΔACQ全等.····························································· 2分
证明:∵ 菱形ABGH、BCFG、CDEF全等,
∴ AB=BC=EF=FG.
∴ AB+BC=EF+FG,即AC=EG.························································· 1分
![]() AD∥HE,∴ ∠QAC=∠PEG.························································ 1分
AD∥HE,∴ ∠QAC=∠PEG.························································ 1分
![]() BG∥CF,∴ ∠AQC=∠EPG.························································ 1分
BG∥CF,∴ ∠AQC=∠EPG.························································ 1分
∴ △EGP≌△ACQ.············································································ 1分
12.(本题12分)
解:(1)① y=![]() .····································································· 2分
.····································································· 2分
当x=60(cm)时,y最大值=1800(cm2);················································ 2分
② 过点B作BE⊥AD于E,CF⊥AD于F,
设AB=CD=xcm,梯形的面积为S cm2,则BC=EF=(120-2x)cm,
 AE=DF=
AE=DF=![]() x,BE=CF=
x,BE=CF=![]() x ,AD=120-x,
x ,AD=120-x,
∴S=![]() ·
·![]() x(240-3x)
x(240-3x)
当x=40,S最大值=1200![]() ,···································································· 2分
,···································································· 2分
S最大值>y最大值·························································································· 2分
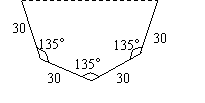
(2)方案正确一个得2分,共4分.

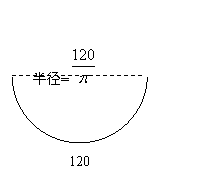 方案:①正八边形的一半,②正十边形的一半,③半圆等
方案:①正八边形的一半,②正十边形的一半,③半圆等
 |