2005学年第一学期初三期末考试卷
数 学
各位同学:
1、本试卷分试题卷和答题卷两部分，考试时间100分钟,满分120分
2、答题前，请在答题卷的密封区内填写学校、班级和姓名
3、可以使用计算器
4、所有答案都必须做在答题卷规定的位置上，注意试题序号的答题序号相对应
试题卷
一、选择题(每小题3分，共30分)
1. 在下列各式: 
，
，
，
，
中，分式的个数是
（A）0 （B）1 （C）2 （D） 3
2.一个袋中装有40个红球，2个黄球和1个白球，现从袋中摸出一个球，那么
(A) 一定摸到红球 (B) 很可能摸到红球
(C) 不会摸到黄球 (D) 不可能摸到白球
3. 方程
的解是
（A）
（B）
（C）
（D）或3
4．下列语句中是真命题的是
(A) 画∠ABC的平分线.
(B) 是方程
的根.
(C) 正方形是中心对称图形吗？ (D) 矩形的对角线相等.
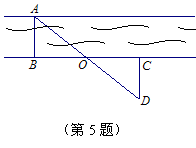5. 小红用如图所示的方法测量小河的宽度.
她利用适当的工具，使AB⊥BC, BO=OC,
CD⊥BC,点A、O、D在同一直线上，就能
保证△ABO≌△CDO,从而可通过测量CD
的长度得知小河的宽度AB.在这个问题中，
可作为证明△ABO≌△CDO的依据的是
（A）S.A.S或A.A.S （B） A.A.S或H.L
（C）A.S.A或A.A.S （D）A.S.A或S.A.S
6. 若一元二次方程ax2+bx+c=0的两根为x1= -3，x2= 1，那么二次函数y=ax2+bx+c图象的对称轴是
（A）x = 1 （B）y轴 （C）x = -1 （D）x = -2
7. 如图，一把折扇打开后是一个圆心角
为120°、面积为
cm2的扇形，那么
这个扇形的半径应为
(A) 10cm (B) 20cm
(C) 
cm (D) 40cm
8．二次函数
配方成
的形式后得
（A） 
（B）
（C） 
（D） 
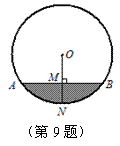
9. 如图是一个下水管的横截面，阴影部分为污水的截面，
若管道的半径为5分米，水面AB的宽度为8分米，则管
道内水深MN为
(A) 4分米 (B) 3分米
(C) 2分米 (D) 1分米
10．⊙A、⊙B、⊙C的位置如图所示，其中⊙B、⊙C是
等圆，若在⊙A内任意画一点P，则点P落在⊙C内的概
率是
（A）
（B）
（C）
（D）
二、填空题（每小题4分，共24分）
11．二次函数 
的图像向下平移1个单位，得到的图像的表达式是
▲ .
12.小南为春节联欢活动设计一个抽奖游戏，在暗箱中放入写有“有奖”或“谢谢”的纸条若干张，活动要求从一个暗箱中任意取出一张纸条正好写着“有奖”的概率是
.现在暗箱中共有3张写着“有奖”的纸条，那么暗箱中应有 ▲
张写有“谢谢”的纸条.
13．我们知道，圆和圆有多种位置关系.如下图中，就有外离、相交和内含等三种，请再写出一种两圆的位置关系如__ ▲_ __.(只需写一种)
 |
14．某路公交车起点站设在一居民小区附近，为了了解高峰时段从该起点站乘车出行的人数，随机抽查了高峰时段10个班次从该起点站乘车的人数，结果如下：
20 23 26 25 29 28 30 25 21 23
如果在高峰时段从该起点站共发车60个班次，估计在高峰时段从该起点站乘该路车出行的乘客一共有 ▲ 人.
15．请写出一个一元二次方程，使它的一个根为1，另一个根满足－3＜x＜0，
如 ▲ .
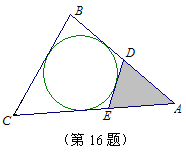16．如图是一块三角形铁皮，其中AB=9，
BC=8，CA=10，工人师傅在△ABC 中取走
一个最大的圆后，为充分利用这块铁皮，
又在余料中裁出一个最大的三角形DEA，
那么，△DEA的周长是 ▲ .
三．解答题（本题有8小题，共66分）
17．（8分）尺规作图， 不写作法，保留作图痕迹.
如图，已知∠ABC，求作：
（1）∠DOE，使∠DOE=∠ABC；
（2）在AB上任取一点P，作直线PQ，使PQ⊥BC.
18．计算（满分9分）（本题有4小题，分值不同，请任选2题计算，多答不加分）
（1）
（4分） （2）
（4分）
（3）
（4分）
（4）先化简后求值：
，其中x=－1（5分）
19．解下列关于方程的问题（满分15分）
（1） 解方程
（5分） （2）解方程 
（5分）
（3）已知关于x的方程
的两个根是0和－3，
求p、 q的值.（5分）
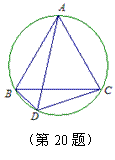
20．（5分）如图，点A、B、C、D在圆上，且△ABC是
等边三角形，则∠BAC=∠ABC=∠ACB=60º,请在图中
再找出一个大小为60º的角，并证明你的结论.
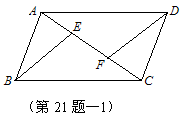
21． 证明题（满分6分）（本题有2小题，分值不同，请任选其中1题进行证明，多答不加分。）
（1）如图，在□ABCD中，E，F是对角线AC上的两点，且AE=CF．
求证：BE=DF．（本题4分）
 |
（2）如图，△ABC中，∠BCA =90º，AC=BC，D为BC的中点，CE⊥AD，垂足为E，BF∥AC交CE的延长线于点F. 求证：AB垂直平分DF.（本题6分）
 |
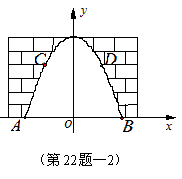
22. （6分）如图，某地一古城墙门洞呈抛物线形，已知门洞的地面宽度AB＝12米，两侧距地面5米高C、D处各有一盏路灯，两灯间的水平距离CD＝8米，求这个门洞的高度. （提示：选择适当的位置为原点建立直角坐标系，例如下右图：以AB的中点为坐标原点建立直角坐标系.）
 |
23．（6分）某校初一、初二两个年级的同学同时从学校出发，步行5千米参观科技园，由于初二年级的同学比初一年级的同学每小时多走1千米，结果初二年级比初一年级早到10分钟，求初一、初二年级的同学每小时各走多少千米.
24．（11分）如图，已知A（0，1）、D（4，3），P是以AD为对角线的矩形ABDC内部（不在各边上）的一个动点，点C在
轴上，抛物线
以P为顶点.
（1）判断以C为圆心、2为半径的圆与直线AD的位置关系 (是 ▲ ) ；
（2）能否判断抛物线的开口方向？请说明理由.
（3）设抛物线与
轴有交点F、E（F在E的左侧），△E AO与
△FAO的面积之差为3，且这条抛物线与线段AD有一个交点的横坐标为
，这时能确定a、b的值吗？若能，请求出a、b的值；若不能，请确定a、b的取值范围.（本题的图形仅供分析参考用）
 |
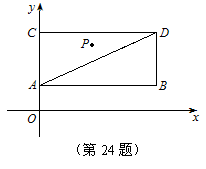