初三数学月考试卷

（满分：120分，时间：100分钟）

	题号 一 二 三 总分 1—15 16—20 21，22 23，24 25，26

一、选择题（每小题3分，共45分）

	题号 1 2 3 4 5 6 7 8 9 10 得分 B A A D D C C C A D 题号 11 12 13 14 15 得分 A C A C D

二、填空题（每小题4分，共20分）

　　16．　400　 　17.　　8　　　18.　　　19.　10：0.5　 　20.　33　　

三、解答题（本题有6小题，共55分）

21．（7分）

原式=，　　　　　　　　  （4分）

当时，原式=.　　 （3分）

22．（8分）

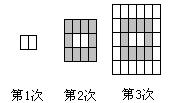（1）第n次铺完时，地板总数为

；（4分）

（2）因为，

所以n=12，正轮到铺第12次.　　　　（4分）

23．（8分）

消去y，得，　　　　　　　　　　　　　　　　　 （4分）

此方程有理化，得，解得（增根），，　　  （2分）

方程组的解是　　　　　　　　　　　　　　　　　　　　  （2分）

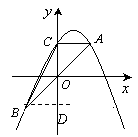24．（10分）

点C，A的坐标分别为（0，c）和（c，c），

点B与A关于原点对称，所以B的坐标为（－c，－c），

　　　　　　　　　　　　　　　　 　　　 （3分）

点A在抛物线上，所以，

　　　　　　　　　　　　　　  （2分）

又因为在抛物线上，所以，化简得

因为，所以　　　　　　　　　　　　 （3分）

所以

25．（10分）

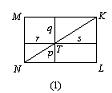
（1）无论何种方法，如，得；（2分）

（2）辅助线如图，设PT=x，CT=y，

因为，所以

；　　 （2分）

因为，所以.　　 （2分）

消去y，得，所以，　　　　 （2分）

所以　　　　　　　　　　　　　  （2分）

26．（12分）

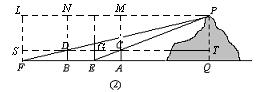
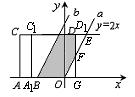
（1）当时，AA₁<4，A₁在B左侧，夹在平行线

之间的部分为五边形（图中阴影部分），面积为平行四边

形面积与△D₁EF面积的差， （2分）

因为点E的横坐标为5，OG=t，F的纵坐标为2t，所以

D₁E=5－t，D₁F=10－2t，

；（2分）

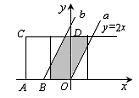
当时，A₁在B右侧，夹在平行线

之间的部分为六边形（图中阴影部分），面积为平行四

边形与左下、右上两个三角形面积的差.　　 （2分）

同理，左下三角形的面积为

，

右上三角形面积为，

所以.（2分）

综上所述，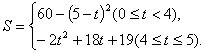

（2）当时的函数没有最大值；

当时，函数可化为，（2分）

所以函数在时，面积达到最大值.（2分）