厦门市2004年初中毕业和高中阶段各类学校招生考试
数 学 试 卷
(满分:A卷100分,B卷50分;考试时间:120分钟)
考生注意:本试卷为A卷填空题和选择题.答题卷为A卷填空题的答题栏、选择题的答题表、A卷的解答题和B卷.考生必须把试卷上试题的答案填在答题卷的相应答题位置上,答在试卷上视为无效.收卷时只收答题卷,试卷由考场统一处理, 请考生不要私自带走.
一、填空题:(本大题共10小题,每小题3分,共30分)(答案须填在答题卷)
1、-3的相反数是 .
2、计算:sin30°= .
 3、已知:∠A=30°,则∠A的补角是_____度.
3、已知:∠A=30°,则∠A的补角是_____度.
4、计算:3x2y+2x2y= .
5、分解因式:ma+mb = .
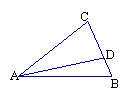
6、已知:如图,D是BC上一点, ∠C=62°, ∠CAD=32°,
则 ∠ADB= 度.
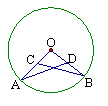 7、已知:如图,OA、OB为⊙O的半径,C、D分别为OA、OB的中点,
7、已知:如图,OA、OB为⊙O的半径,C、D分别为OA、OB的中点,
若AD=3厘米,则BC= 厘米.
8、已知一条弧的长是3![]() 厘米, 弧的半径是6厘米,则这条弧
厘米, 弧的半径是6厘米,则这条弧
所对的圆心角是 度(弧长公式:l = ).
9、为鼓励节约用电,某地对居民用户用电收费标准作如下规定:每户每月用电如果不超过100度,那么每度电价按a元收费;如果超过100度,那么超过部分每度电价按b元收费.某户居民在一个月内用电160度,他这个月应缴纳电费是 元(用含a、b的代数式表示).
10、矩形ABCD中,M是BC边上且与B、C不重合的点,点P是射线AM上的点,若以A、P、D为顶点的三角形与△ABM相似,则这样的点有 个.
二、选择题:(本大题共5小题,每小题4分,共20分)(答案须填在答题卷)
每小题都有四个选项,其中有且只有一个选项是正确的,请将正确选项的字母代号填写在答题卷上的答题表中相应的空格内,选对每小题得4分,选错、不选或多选均得0分.
11、下列计算正确的是
(A)·= (B) +=
(C) =3 (D) ÷=2
12、已知在⊙O中,弦AB的长为8厘米,圆心O到AB的距离为3厘米, 则⊙O的半径是
 (A)3厘米 (B) 4厘米
(A)3厘米 (B) 4厘米
(C) 5厘米 (D) 8厘米
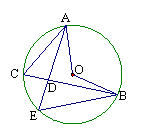
13、已知:如图, ⊙O的两条弦AE、BC相交于点D,连结AC、BE.
若∠ACB=60°,则下列结论中正确的是
(A) ∠AOB=60° (B) ∠ADB=60°
(C) ∠AEB=60° (D) ∠AEB=30°
14、一定质量的干松木,当它的体积V=2m3时,它的密度ρ=0.5×103kg/m3,
则ρ与V的函数关系式是
(A) ρ=1000V (B) ρ=V+1000
(C) ρ= (D) ρ=
15、矩形ABCD中的顶点A、B、C、D按顺时针方向排列,若在平面直角坐标系内, B、D 两点对应的坐标分别是(2, 0), (0, 0),且 A、C两点关于x轴对称.则C 点对应的坐标是
(A)(1, 1) (B) (1, -1)
(C) (1, -2) (D) (, -)
本页空白,可作为草稿纸.
本页空白,可作为草稿纸.
厦门市2004年初中毕业和高中阶段各类学校招生考试
数 学 答 题 卷
(满分:A卷100分,B卷50分;考试时间:120分钟)
| 题号 | 一 | 二 | 三 | A卷 | 全卷 | |||||||
| 1~10 | 11~15 | 16 | 17 | 18 | 19 | 20 |
|
| ||||
| 得分 |
|
|
|
|
|
|
| |||||
| 复核 |
|
|
|
|
|
|
|
| ||||
| 题号 | 四 | 五 | B卷 | |||||||||
| 21~24 | 25 | 26 | 27 | 28 |
| |||||||
| 得分 |
|
|
|
|
| |||||||
| 复核 |
|
|
|
|
|
|
| |||||
A卷
一、填空题答题栏:(本大题共10小题,每小题3分,共30分)
| 得分 | 评 卷 人 |
|
|
1、 . 2、 . 3、 度. 4、 .
5、 . 6、 度. 7、 厘米.
8、 度. 9、 元. 10、 个.
二、选择题答题表:(本大题共5小题,每小题4分,共20分)
| 题号 | 11 | 12 | 13 | 14 | 15 |
| 选项 |
| 得分 | 评 卷 人 |
|
|
三、解答题:(本大题共5小题,每小题10分,共50分)
| 得分 | 评 卷 人 |
16、(本题满分10分)
解不等式组 并把解集在数轴上表示出来.
 |
| 得分 | 评 卷 人 |
17、(本题满分10分)
解方程组
| 得分 | 评 卷 人 |
18、(本题满分10分)
(1) 甲品牌拖拉机开始工作时,油箱中有油30升.如果每小时耗油6
升,求油箱中的余油量y(升)与工作时间x(时)之间的函数关系式.
 (2) 如图,线段AB表示乙品牌拖拉机在工作时油箱中的余油量y(升)与工作时间x(时)之间的函数关系的图象. 若甲、乙两种品牌的拖拉机在售价、质量、
(2) 如图,线段AB表示乙品牌拖拉机在工作时油箱中的余油量y(升)与工作时间x(时)之间的函数关系的图象. 若甲、乙两种品牌的拖拉机在售价、质量、
性能、售后服务等条件上都一样.根据图象提供的信息,你愿意
购买哪种品牌的拖拉机,并说明理由.
| 得分 | 评 卷 人 |
19、(本题满分10分)
如图,已知在等腰梯形ABCD中,AD∥BC.
(1) 若AD=5, BC=11,梯形的高是4,求梯形的周长.
 (2)
若AD=a, BC=b, 梯形的高是h,梯形的周长为c.
(2)
若AD=a, BC=b, 梯形的高是h,梯形的周长为c.
则c= .
(请用含a、b、h的代数式表示; 答案直接写在横线上,不要求证明.)
(3)若AD=3, BC=7, BD=5,求证:AC⊥BD.
| 得分 | 评 卷 人 |
20、(本题满分10分)
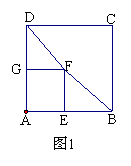
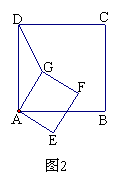
已知正方形ABCD和正方形AEFG有一个公共点A,点G、E分别在线段AD、AB上.
(1) 如图1, 连结DF、BF,若将正方形AEFG绕点A按顺时针方向旋转,判断命题:“在旋转的过程中线段DF与BF的长始终相等.”是否正确,若正确请证明,若不正确请举反例说明;
(2) 若将正方形AEFG绕点A按顺时针方向旋转, 连结DG,在旋转的过程中,你能否找到一条线段的长与线段DG的长始终相等.并以图2为例说明理由.
 |
 |
B卷
四、填空题:(本大题共4小题,每小题3分,共12分)
| 得分 | 评 卷 人 |
21、 计算: - = .
22、已知正四边形ABCD的半径是,则它的面积是 .
23、我们知道2003年10月我国成功地发射了第一艘载人飞船.下面是关于“神舟五号载人飞船”在太空中飞行的一段报道:
15日15时57分,据航天员杨利伟报告和地面监测表明“神舟五号载人飞船”变轨成功.据北京航天指挥控制中心现场工作人员介绍,飞船发射升空后,进入的是绕地球飞行的椭圆轨道.实施变轨后,飞船进入的是距地球表面约343千米的圆形轨道.
看完上面的这段报道,请你说出“神舟五号载人飞船”变轨后的轨迹是:
.(地球的半径约为6371千米)
24、已知关于x的方程x2-(a+b)x+ab-2=0. x1、x2是此方程的两个实数根,现给出三个结论:
(1) x1≠x2 (2) x1x2>a b (3 ) x12+x22>a2+b2
则正确结论的序号是 .(在横线上填上所有正确结论的序号)
五、解答题:(第25、26题每题8分, 第27题10分,第28题12分,共38分)
| 得分 | 评 卷 人 |
25、(本题满分8分)
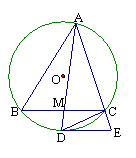
如图,在△ABC中,∠A的平分线AM与BC交于点M,且与△ABC的外接圆O交于点D.过D作⊙O的切线交AC的延长线于E,
连结DC, 求证: .
要求:请根据题目所给的条件和图形,在题中的横线上写出一个正确的结论,并加以证明(在写结论和证明时都不能在图中添加其它字母和线段).按证明结论时需要用到的已知条件的多少给分,若用足已知条件而证得结论即可得满分.
 |
| 得分 | 评 卷 人 |
26、(本题满分8分)
为了从甲、乙两名同学中选拔一人参加射击比赛,在同等的条件下,教练给甲、乙两名同学安排了一次射击测验, 每人打10发子弹,下面是甲、乙两人各自的射击情况记录(其中乙的情况记录表上射中9、10环的子弹数被墨水污染看不清楚,但是教练记得乙射中9、10环的子弹数均不为0发):
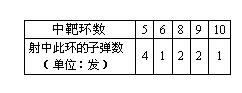 甲: 乙:
甲: 乙:
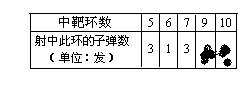 |
(1)求甲同学在这次测验中平均每次射中的环数;
(2) 根据这次测验的情况,如果你是教练,你认为选谁参加比赛比较合适,并说明理由(结果保留到小数点后第1位).
| 得分 | 评 卷 人 |
27、(本题满分10分)
已知抛物线y=ax2+(b-1)x+2.
(1)若抛物线经过点(1,4)、(-1,-2), 求此抛物线的解析式;
(2) 若此抛物线与直线y=x有两个不同的交点P、Q,且点P、Q关于原点对称.
① 求b的值;
② 请在横线上填上一个符合条件的a的值: a = ,并在此条件下画出该函数的图象.
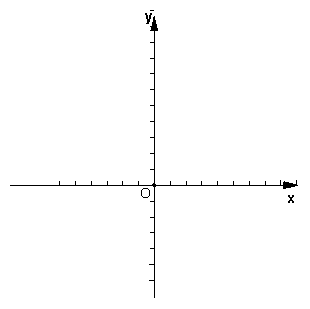
| 得分 | 评 卷 人 |
28、(本题满分12分)
已知圆心在原点,半径为1的⊙O,直线AB与⊙O切于点P (m,n). 且与x、y轴交于点A(a,0)、B(0,b) (a>0,b>0).
(1) 如图1,当 m = 时,求a的值;
(2) 如图2,连结OP,过P向x轴引垂线交x轴于点C,设x表示△OPC的面积,y=a+b, 试求y与x之间的函数关系式,并写出自变量x的取值范围.
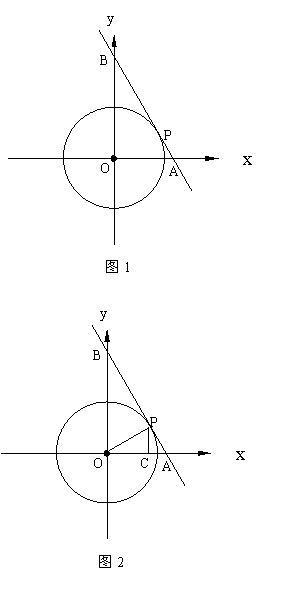 |