2004年龙岩市初中毕业、升学考试
数学试题
(满分:150分 考试时间120分钟)
一、填空题(本题共12小题,每小题3分,计36分.)
1. ![]() 的相反数是__________.
的相反数是__________.
2. 因式分解:![]() =__________.
=__________.
 3. 2004年4月6日《闽西日报》刊载:龙岩市统计局公布去年我市各级各类学校在校生约为620000人,用科学记数法表示为__________人.
3. 2004年4月6日《闽西日报》刊载:龙岩市统计局公布去年我市各级各类学校在校生约为620000人,用科学记数法表示为__________人.
4.
当![]() 时,分式
时,分式![]() 的值为零.
的值为零.
5.
函数![]() 的自变量
的自变量![]() 的取值范围是__________.
的取值范围是__________.
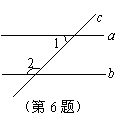
6. 如图所示,![]() ,c与a、b相交,若
,c与a、b相交,若![]() ,则
,则![]() =__________度.
=__________度.
7. 正八边形的每一个外角等于__________度.
8. 小明的身高是1.6m,他的影长是2m,同一时刻旗杆的影长是15m,则旗杆的高是__________m.
9.
 装修工人拟用某种材料包装圆柱体的石柱侧面,现量得石柱底面周长约为0.9m,柱高约为3m,那么至少需用该材料 m2.
装修工人拟用某种材料包装圆柱体的石柱侧面,现量得石柱底面周长约为0.9m,柱高约为3m,那么至少需用该材料 m2.
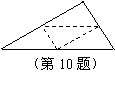
10. 把一块周长为20cm的三角形铁片裁成四块形状、大小完全
相同的小三角形铁片(如图示),则每块小三角形铁片的周
![]()
 长为 cm.
长为 cm.
11.
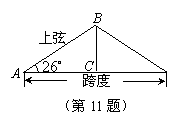
如图,厂房屋顶人字架(等腰三角形)的跨度为12m,![]() ,
,
则中柱BC(C为底边中点)的长约为 m.(精确到
0.01m)
12.
若a、b满足![]() ,则
,则![]() 的值为 .
的值为 .
二、选择题(本题共8小题,每小题4分,计32分;每小题都给出四个备选答案,其中有且只有一个是正确的,把正确答案的代号填入下表中)
13. 下列各式中,运算正确的是
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
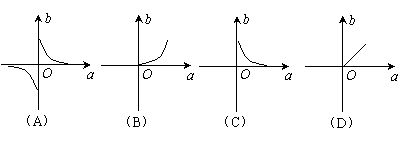
14. 若矩形的面积S为定值,矩形的长为a,宽为b,则b关于a的函数图象大致是
15. 某商品标价1200元,打八折售出后仍盈利100元,则该商品进价是
(A)800元 (B)860元 (C)900元 (D)960元
16.
计算![]() 的结果为
的结果为
(A)0
(B)1
(C) -3 (D)![]()
17. 顺次连结等腰梯形各边中点所得四边形是
(A)梯形 (B)矩形 (C)菱形 (D)正方形
18. 商店里出售下列形状的地砖:1正三角形 2正方形 3正五边形 4正六边形,只选购
其中一种地砖镶嵌地面,可供选择的地砖共有
(A)1种 (B)2种 (C)3种 (D)4种
19. 在半径为2a的⊙O中,弦AB长为![]() ,则
,则![]() 为
为
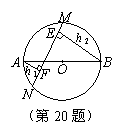 (A)
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
19. 如图,AB是⊙O的直径,且AB=10,弦MN的长为8,若弦
MN的两端在圆周上滑动时,始终与AB相交,记点A、B到
MN的距离分别为h1、h2,则 h 1- h 2等于
(A)5 (B)6
(C)7 (D)8
三、解答题:(共大题共8小题,计82分)
21. (9分)先化简,再求值:![]() ,其中
,其中![]() .
.
22.
 (9分)今年4月25日,我市举行龙岩冠豸山机场
(9分)今年4月25日,我市举行龙岩冠豸山机场
首航仪式,利用这一契机,推出“冠豸山绿色之旅”
等多项旅游项目.“五一”这天,对连城八家旅行社
中部分游客的年龄(年龄取整数)进行了抽样统计,
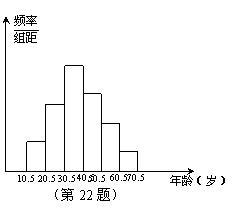
经整理后分成六组,并绘制成频率分布直方图(如
图示).已知从左到右依次为1~6小组的频率分别
是0.08 、0.20、0.32、0.24、0.12 、0.04,第1小
组的频数为8,请结合图形回答下列问题:
(1)这次抽样的样本容量是 ;
(2)样本中年龄的中位数落在第 小组内;
(3)“五一”这天,若到连城豸的游客约有5000人,请
你用学过的统计知识去估计20.5)~50.5年龄段的
游客约有 人.
23. 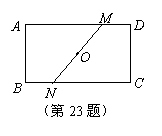 (8分)如图,ABCD是一张矩形纸片,点O为矩形对角线的交点.直线MN经过点O交AD于M,交BC于N.
(8分)如图,ABCD是一张矩形纸片,点O为矩形对角线的交点.直线MN经过点O交AD于M,交BC于N.
操作:先沿直线MN剪开,并将直角梯形MNCD绕点O旋
转 度后(填入一个你认为正确的序号:1![]() ;
;
2![]() ;3
;3![]() ;4
;4![]() ),恰与直角梯形NMAB完全重
),恰与直角梯形NMAB完全重
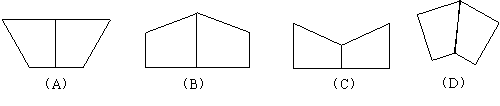
合;再将重合后的直角梯形MNCD以直线MN为轴翻转![]()
后所得到的图形是下列中的 .(填写正确图形的代号)
 |
24. (10分)张老师在一次“探究性学习”课中,设计了如下数表:
| n | 2 | 3 | 4 | 5 | … |
| a | 22-1 | 32-1 | 42-1 | 52-1 | … |
| b | 4 | 6 | 8 | 10 | … |
| c | 22+1 | 32+1 | 42+1 | 52+1 | … |
(1) 请你分别观察a、b、c与n之间的关系,并用含自然数n (n>1)的代数式表示:
a = ,b = ,c = .
(2)猜想:以a、b、c为边的三角形是否为直角三角形?并证明你的猜想.
25. (10分)已知关于x的方程![]() 的两实根x1、x2满足: x1+ x2=2,试求k的值.
的两实根x1、x2满足: x1+ x2=2,试求k的值.
26. (10分)为加强公民节约用水,减少污水排放的环保意识,某城市制定了以下用水收费标准(含城市污水处理费):每户每月用水未超过8 m3时,按1.2元/ m3收费;每户每月用水超过8 m3时,其中的8 m3仍按原标准收费,超过部分按1.9元/m3收费.设某户每月用水量为x(m3),应交水费为y(元).
(1)分别写出用水未超过8m3和超过8m3时,y与x之间的函数关系式;
(2)某用户五月份共交水费13.4元,问该用户五月份用水多少m3.
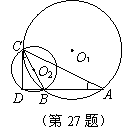 27. (12分)如图,已知⊙O1为△ABC的外接圆,以BC为直径作⊙O2,交AB的延长线于D,连结CD,且∠BCD=∠A.
27. (12分)如图,已知⊙O1为△ABC的外接圆,以BC为直径作⊙O2,交AB的延长线于D,连结CD,且∠BCD=∠A.
(1)求证:CD为⊙O1的切线;
(2)如果CD=2,AB=3,试求⊙O1的直径.
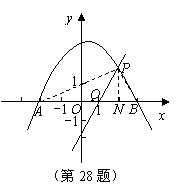
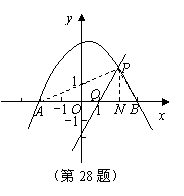
28. (14分)如图,已知抛物线C:![]() 与x轴交于点A、B两点,过定点的直线l:
与x轴交于点A、B两点,过定点的直线l:![]() 交x轴于点Q.
交x轴于点Q.
(1)求证:不论a取何实数(a≠0)抛物线C与直线l总有两个交点;
(2)写出点A、B的坐标:A( , )、B( , )及点Q的坐标;Q( , )(用含a的代数式表示);并依点Q坐标的变化确定:当 时(填上a的取值范围), 直线l与抛物线C在第一象限内有交点;
(2)  设直线l与抛物线C在第一象限内的交点为P,是否存在这样的点P,使得∠APB=90°?若存在,求出此时a的值;不存在,请说明理由.
设直线l与抛物线C在第一象限内的交点为P,是否存在这样的点P,使得∠APB=90°?若存在,求出此时a的值;不存在,请说明理由.
2004年龙岩市初中毕业、升学考试
参考答案及评分标准
一、填空题(每小题3分,共36分)
1. 3; 2. x (x -1)( x +1); 3. 6.2×105; 4. 2;
5. x≥-2; 6. 130; 7. 45; 8. 12;
9. 2.7; 10.
10;
11.2.93;
12. ![]()
二、选择题(本大题共4小题,计32分)
| 题号 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 答案 | D | C | B | A | C | C | B | B |
三、解答题(本大题共8小题,计82分)
21. (9分)解:原式=![]() ………………………………………………(2分)
………………………………………………(2分)
=![]()
=![]() …………………………………………………………(6分)
…………………………………………………………(6分)
当![]() 时,
时,
原式=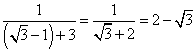 ………………………………………………(9分)
………………………………………………(9分)
22. (9分)(1)100 (2)3 (3)3800……………………………………(每空3分)
23. (8分)2; (D)………………………………………………………(每空4分)
24. (10分)(1)n2-1 2 n n2+1…………………………………(每空2分,计6分)
(2)答:以a、b、c为边的三角形是直角三角形…………………………………(7分)
证明:∵a2+ b2=(n2-1)2+4 n2
= n4-2 n2+1+4 n2= n 4+2 n2+1=( n2+1)2=c2
∴以a、b、c为边的三角形是直角三角形……………………………(10分)
25. (10分)解法一:依题意,![]() ,所以x1与x2同号……(2分)
,所以x1与x2同号……(2分)
1. 当x1>0,x2>0时,有x1+ x2=2,即k+1=2,k=1无解。
2. 当x1<0,x2<0时,有-( x1+ x2)=2,即k+1=-2,k=-3…………………………(6分)
Δ=[-4(k+1)]2-16(k2+1)=32k ………………………………………………………(7分)
当k =1时,Δ>0符合题意;
当k =-3时,Δ<0舍去。
所以,满足题意的k的值为1………………………………………………………(10分)
解法二:依题意,Δ=[-4(k+1)]2-16(k2+1)=32k≥0,即k≥0………………(2分)
于是x1+ x2=k+1>0………………………………………………………………(4分)
又![]()
∴x1>0,x2>0……………………………………………………………………(7分)
由 x1+ x2=2,得x1+ x2=2
k+1=2,解得k=1。
所以,满足题意的k的值为1。………………………………………………(10分)
26. (10分)解:(1)当x≤8时,y=1.2x……………………………………(3分)
当x>8时,y=1.9x-5.6…………………………………(6分)
(写成y=8×1.2+(x-8)×1.9,不扣分)
(2)∵8×1.2=9.6<13.4
∴y=13.4应满足y=1.9x-5.6
∴13.4=1.9x-5.6 解得x=10…………………………………………………(9分)
答:该用户五月份用水10m3 .
27. (12分)(1)证法一:过点C作
⊙O1的直径CE,并连接
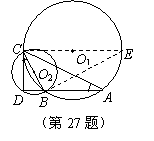 BE………………………………(1分)
BE………………………………(1分)
∵∠BCE=∠A,∠E=∠A
∴∠BCD=∠………………………(3分)
∵CE为⊙O1的直径
∴∠CBE=…………………………(4分)
∴∠E+∠ECB=90°
∴∠BCD+∠ECB=90°
即EC⊥CD
∴CD为⊙O1的切 ………………(6分)
证法二:过C作⊙O1的直径CE,连AE,利用圆内接四边形的外角的性质进行证明。
证法三:连OO1、O1O2并延长O1O2交![]() 于点M,利用圆心角关系进行证明。
于点M,利用圆心角关系进行证明。
(2)解法一:∵CD为⊙O1的切线
∴CD2=DB·DA=DB·(DB+AB)由CD=2,AB=3
解得DB=1,DB=-4(舍去)…………………………………(8分)
∵CB为⊙O2的直径
∴∠D=90°,则![]() ……(9分)
……(9分)
∴△BCD∽△CEB
∴![]()
∴![]() ,解得CE=5……………………………………(12分)
,解得CE=5……………………………………(12分)
解法二:在求出DB=1的基础上,过O作OF⊥AB垂足为F,由四边形O1CDF是矩形进行解答;
解法三:在求出DB=1的基础上,由△O1O2C∽△COB可求出半径;
解法四:在求出DB=1的基础上,根据勾股定理,求AC;由△CDB∽△CAE可求出直径。
 28. (14分)
28. (14分)
(1)证明:由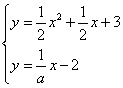 消去y,得
消去y,得
![]()
![]() ……………………………………………………(2分)
……………………………………………………(2分)
∴不论a(a≠0)取何实数,方程组有两组不同的实数解,故不论a(a≠0)取何实数,抛物线C与直线l总有两个交点……………………………………(3分)
(2)A(-2,0),B(3,0),Q(2a,0)………………(每点坐标1分,共6分)
![]() (写成a>0或a<
(写成a>0或a<![]() 只能给1分)…………………………………(8分)
只能给1分)…………………………………(8分)
(3)设存在满足条件的点P(x0,y0)(x0>0,y0>0),连AP、PB,使∠APB=90° ,作PN⊥AB于N,则AN= x0+2,BN=3- x0,PN= y0
∵∠APB=90°,PN⊥AB,则△APN∽△PBN。
∴PN2=AN·BN,则有![]() =( x0+2)(3- x0)
=( x0+2)(3- x0)
即![]() =-
=-![]() + x0+6 1………………………………………………………(11分)
+ x0+6 1………………………………………………………(11分)
∵点P(x0,y0)在抛物线C上
∴![]() 即
即![]() 2
2
由1、2可得![]() ………………………………(13分)
………………………………(13分)
把![]() 代入2,得
代入2,得![]() 或-1,
或-1,![]()
把![]() 代入
代入![]() ,得
,得![]()
∴存在满足条件的P点,此时![]() ……………………………………(14分)
……………………………………(14分)
二、设存在满足条件的点P(x0,y0),连PA、PB,使∠APB=90°
在Rt△APB中,斜边的中点![]() ,过点P作PN⊥AB,垂足为N,N的坐标为(x0,0),连接PM,由Rt△PMN,得MN2+PN2=PM2
,过点P作PN⊥AB,垂足为N,N的坐标为(x0,0),连接PM,由Rt△PMN,得MN2+PN2=PM2
![]()
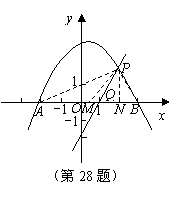 由
由 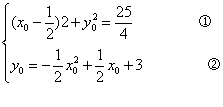
整理,得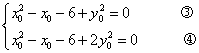
3-4得,![]() ……
……
三、设存在满足条件的点P(x0,y0),连PA、PB,使∠APB=90°
 过点P作PN⊥AB,垂足为N,根据勾股定理得
过点P作PN⊥AB,垂足为N,根据勾股定理得
![]()
即![]()
整理得![]()
解方程组: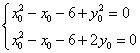 ……
……
