北京市高级中等学校招生统一考试(海淀卷)
数学试卷
考生须知:
1. 本试卷共4页,28道题;满分120分;考试时间120分钟。
2. 试题答案一律填涂、书写在答题卡上,在试卷上作答无效。
3. 认真填写学校名称、姓名和准考证号。
4. 解题前,请认真阅读答题卡的要求,按要求解答。解答题要写明主要步骤,结果必须明确。
5. 作答用笔要求请见答题卡。
一. 选择题:(本题共40分,第1~8题各3分,第9~12题各4分)
在下列各题的四个备选答案中,只有一个是正确的。
1. 图1是圆规示意图,张开的两脚所形成的角是( )
A. 平角 B. 钝角 C. 直角 D. 锐角

图1
![]()
![]()
3. 从“第二届互联网大会”上获悉,中国的互联网上网用户已超过7800万,居世界第二位。7800万用科学记数法表示为( )
A. 7.8×106 B. 7.8×107 C. 7.8×108 D. 0.78×108
![]()
![]()
![]()
5. 下列各运算中,结果正确的是( )
![]()
![]()
![]()
![]()
![]()
7. 若两个圆只有两条公切线,则这两个圆的位置关系是( )
A. 外离 B. 相交 C. 内切 D. 内含
![]()
A. 5 B. 4 C. 3 D. 2
![]()
![]()
10. 如图2所示,在圆O中,AB为弦,OC⊥AB,垂足为C。若AO=5,OC=3,则弦AB的长为( )
A. 10 B. 8 C. 6 D. 4
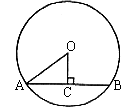
图2
11. 多项式ac-bc+a2-b2分解因式的结果是( )
![]()
![]()
![]()
![]()
12. 图3是饮水机的图片。饮水桶中的水由图4的位置下降到图5的位置的过程中,如果水减少的体积是y,水位下降的高度是x,那么能够表示y与x之间函数关系的图象可能是( )

图3 图4 图5
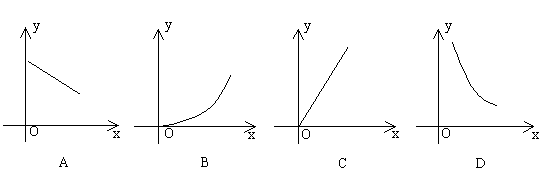
二. 填空题:(本题共28分,第13~19题每空3分,第20题4分)
13. 已知梯形中位线的长为6,下底的长为7,那么上底的长为______________。
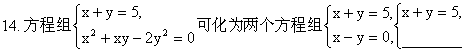
15. 下表是食品营养成份表的一部分(每100克食品中可食部分营养成份的含量)

在表中提供的碳水化合物的克数所组成的数据中,中位数是______________,平均数是______________。
![]()
17. 如果圆柱的底面半径为3cm,母线长为3cm,那么这个圆柱的侧面展开图的面积是______________cm2。
18. 某课外活动小组的同学在研究某种植物标本(如图6所示)时,测得叶片①最大宽度是8cm,最大长度是16cm;叶片②最大宽度是7cm,最大长度是14cm;叶片③最大宽度约为6.5cm,请你用所学数学知识估算叶片③的完整叶片的最大长度,结果约为_______________cm。

图6
![]() 为________________。
为________________。
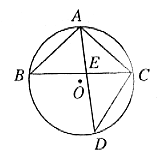
图7
20. 观察下列各等式:
![]()
![]()
![]()
![]()
依照以上各式成立的规律,在括号中填入适当的数,使等式![]()
三. (本题共23分,第21题5分,第22~24题各6分)
![]()
![]()
23. 已知:如图8所示,在菱形ABCD中,E、F分别是BC、CD上的点,且CE=CF。
![]()
(2)过点C作CG//EA交AF于H,交AD于G。若∠BAE=25°,∠BCD=130°,求∠AHC的度数。
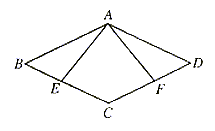
图8
24. 已知:如图9所示,梯形ABCD中,AD//BC,BD平分∠ABC,∠A=120°,![]()
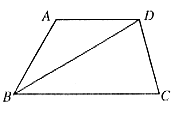
图9
四. (本题共13分,第25题6分,第26题7分)
25. 列方程(组)解应用题:
在某校举办的足球比赛中规定:胜一场得3分,平一场得1分,负一场得0分。某班足球队参加了12场比赛,共得22分。已知这个队只输了2场,那么此队胜几场?平几场?
26. 已知:关于x的一元二次方程ax2+2ax+c=0的两个实数根之差的平方为m。
![]() 明理由;
明理由;
(2)若对于任意一个非零的实数a,m≥4总成立,求实数c及m的值。
五. (本题共16分,第27、28题各8分)
27. 已知:如图10所示,A、K为圆O上的两点,直线FN⊥MA,垂足为N,FN与圆O相切于点F,∠AOK=2∠MAK。
(1)求证:MN是圆O的切线;
(2)若点B为圆O上一动点,BO的延长线交圆O于点C,交NF于点D,连结AC并延长交NF于点E。当FD=2ED时,求∠AEN的余切值。
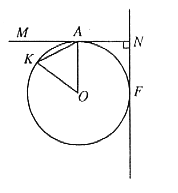
图10
28. 已知:在平面直角坐标系中,点O为坐标原点,点A的坐标为(0,2),以OA为直径作圆B。若点D是x轴上的一动点,连结AD交圆B于点C。
![]()
(2)过点D作DP//y轴与过B、C两点的直线交于点P,请任意求出三个符合条件的点P的坐标,并确定图象经过这三个点的二次函数的解析式;
(3)若点P满足(2)中的条件,点M的坐标为(-3,3),求线段PM与PB的和的最小值,并求出此时点P的坐标。
北京市2004年高级中等学校招生统一考试(海淀卷)
数学试题参考答案及评分标准
一. 选择题:(本题共40分,第1~8题各3分,第9~12题各4分)
1. D 2. A 3. B 4. C 5. D
6. A 7. B 8. C 9. B 10. B
11. A 12. C
二. 填空题:(本题共28分,第13~19题每空3分,第20题4分)
13. 5 14. x+2y=0 15. 4,4
16. 9 17. 18π 18. 13
19. 2 20. -12,-12
三. (本题共23分,第21题5分,第22~24题各6分)
21. 解:![]()
![]()
![]()
![]()
22. 解:方法一:方程两边同乘以x(x+1),得
![]()
整理得4x=1
![]()
![]()
![]()
方法二:![]()
![]()
![]()
![]()
![]()
![]()
去分母,得x+1=5x,
![]()
![]()
![]()
23. (1)证明:![]()
![]()
![]()
![]()
![]()
![]()
(2)解:![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
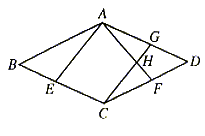
图1
24. 方法一:过点B作BE⊥DA交DA的延长线于E。 1分
![]()
![]()
![]()
![]()
![]()
![]()
![]()
在Rt△BDE中,
![]()
![]()
在Rt△BEA中,
![]()
![]()
![]()
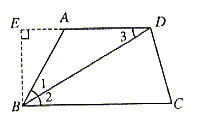
图2
方法二:过点A作AE⊥BD于E,过点D作DF⊥BC于F。 1分
∵BD平分∠ABC
∴∠1=∠2
∵AD//BC,
∴∠3=∠2
∴∠1=∠3
∴AB=AD
∵∠BAD=120°
∴∠2=∠3=∠1=30° 2分
![]()
![]()
![]()
![]()
![]()

图3
四. (本题共13分,第25题6分,第26题7分)
25. 解:设这支足球队胜x场,平y场。 1分
依题意,得
![]()
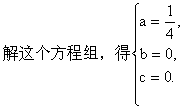
解这个方程组,得
![]()
答:这支足球队胜了6场,平了4场。 6分
26. 解:![]()
![]()
![]()
![]()
即m≥4成立。
![]()
![]()
![]()
![]()
![]()
(2)依题意,设原方程的两个实数根是x1,x2,
![]()
![]()
![]()
![]()
![]()
![]()
五. (本题共16分,第27、28题各8分)
27. (1)证明:如图4所示,延长AO交圆O于G,连结KG,则AG为直径。
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
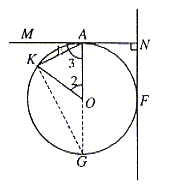
图4
(2)解:依题意,分两种情况:
情况一:如图5所示,连结AB,OF。
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
设圆O的半径为r,ED=x。
![]()
![]()
![]()
![]()
![]()

图5
情况二:如图6所示,设圆O的半径为r,ED=x。
![]()
![]()
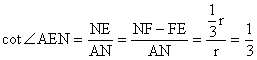
![]()
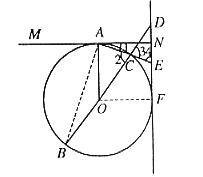
图6
28. 解:(1)如图7所示,当点D在x轴的正半轴上时,连结OC,过C点作CK⊥y轴于点K。
![]()
![]()
![]()
![]()
![]()
设OK的长为x,则KC=2x,可得AK=4x
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
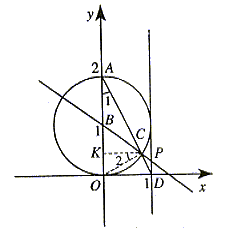
图7
(2)∵DP//y轴,
![]()
当点D位于如图7的位置时,有D(1,0)。
![]()
![]()
如图8所示,当点D的坐标为(2,0)时,△AOD为等腰三角形。
连结OC,
![]()
![]()
![]()
![]()
![]()
![]()
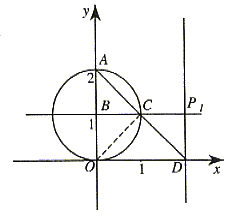
图8
如图9所示,类似地,可得点P2的坐标为(-2,1)
![]()
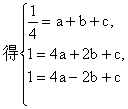
![]()
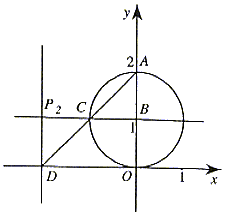
图9
(3)如图10所示,∵AB//PD,
![]()
![]()
![]()
![]()
![]()
由几何知识可知,当直线DP经过点M(-3,3)时,PM+PD的值最小。
![]()
∴当直线DP过点M时,PM+PB的值最小。
∴PM+PB的最小值是MD+BC=3+1=4 7分
∵OD=3,OA=2
![]()
又可证DO是圆B的切线。
![]()
![]()
![]()
![]()
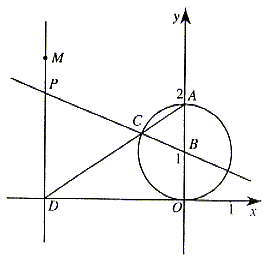
图10