2005年中考数学模拟试题（2）

一、选择题（本题40分，每小题4分）

在下列各题的四个备选答案中，只有一个是正确的，请你将正确答案前的字母填在题后的括号内。

1．－6的绝对值是（　　）。
A. －6　　　　　 B. 6　　　　　 C. －　 　　　　D.

2．9的平方根是（　　）。
A. 3　　　　　　 B. －3　　　　 C. ±3　　　　　　　D. 81

3．有下面命题：(1)直角三角形的两个锐角互余；(2)钝角三角形的两个内角互补；(3)正方形的两条对角线相等；(4)菱形的两条对角线互相垂直。
　 其中，正确的命题有（　　）。
　　A. 1个　　 　　　 B. 2个　　　 

　　C. 3个　　 　　　 D. 4个

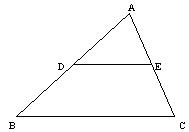
4．如图，DE是DABC的中位线，则DADE与DABC面积的比是（　　）。
　 A. 1：1　　　 　　 B. 1：2　　

 C. 1：3　　　　　　D. 1：4
 

5．用科学记数法表示0.00032，正确的是（　　）。
A. 　　 B. 　　 C. 　　 D.

6．计算，结果正确的是（　　）。
A. 　　　　　 B. 　　　　　　C. 　　　　　　D.

7．在下列图形中，既是中心对称图形又是轴对称图形的是（　　）。
A. 等腰三角形　　B. 圆　 　　　　 C. 梯形　　 　　　D. 平行四边形

8．在函数中，自变量x的取值范围是（　　）。
A. x>1　 　　　　B. x³1　 　　　　　C. x<1　　　　　　 D. x£1

9．对于正比例函数，当x增大时，y随x增大而增大，则m的取值范围是（　　）。
　　　A. m<0　　　　　B. m£0　 　　　　　C. m>0　　　　　　 D. m³0

10．已知两个圆只有一条公切线，那么这两个圆的位置关系是（　　）。
A. 内切　 　　　B. 外切　 　　　　 C. 相交 　　　　　 D. 外离

二、填空题（本题15分，每小题3分）

11．点P（4，3）关于原点的对称点P’的坐标是____________。

12．若，则锐角α=_________度。

13．某校为了了解初一年级300名学生每天完成作业所用时间的情况，从中对20名学生每天完成作业作用时间进行了抽查，这个问题中的样本容量是_______ 。

14．若正多边形的内角和是540°，那么这个多边形一定是正__________边形。

15．若一个圆锥的母线长是5cm，底面半径是3cm，则它的侧面展开图的面积是_____。

三、（本题26分，经16、17小题各6分，第18、19小题各7分）

16．分解因式：。

17．计算：。

18．先化简，再求值：
。

19．解不等式组，并在给定的数轴上表示出解集。

四、（本题12分，每小题6分）

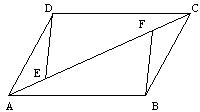20．已知：如图，在平行四边形ABCD中，E、F是对角线AC上的两点，且AF=EC。
　　求证：DE=BF。

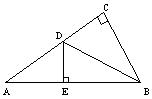21．已知：如图，在DABC中，ÐC=90°，AB的垂直平分线交AC于D，垂足为E。若ÐA=30°，DE=2，求ÐDBC的度数和CD的长。

五、（本题12分，每小题6分）

22．用换元法解方程。

23．列方程或方程组解应用题：

甲、乙两组工人合作完成一项工程，合作5天后，甲组另有任务，由乙组再单独工作1天就可完成。若单独完成这项工程乙组比甲组多用2天，求甲、乙两组单独完成这项工程各需要多少天。

六、（本题12分，每小题6分）

24．已知一次函数的图象与反比例函数的图象相交，其中有一个交点的纵坐标为－4，求这两个函数的解析式。

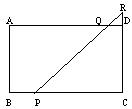25．如图，在矩形ABCD中，AB=4，BC=7，P是BC边上与B点不重合的动点，过点P的直线交CD的延长线于R，交AD于Q（Q与D不重合），且ÐRPC=45°。设BP=x，梯形ABPQ的面积为y，求y与x之间的函数关系，并求出自变量x的取值范围。

七、（本题6分）

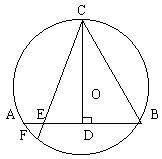26．已知：如图，在⊙O中，CD过圆心O，且CD^AB，垂足为D，过点C任作一弦CF交⊙O于F，交AB于E。
　　求证：。

八、（本题7分）

27．已知关于x的方程(1)只有整数根，且关于y的一元二次方程(2)有两个实数根。
　　(1)当k为整数时，确定k的值；
　　(2)在(1)的条件下，若m>－2，用关于m的代数式表示。

九、（本题9分）

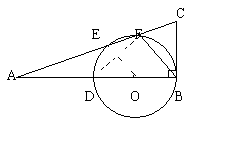
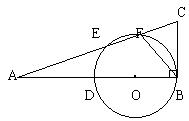28．如图，在RtDABC中，ÐABC=90°，O是AB上的一点，以O为圆心，以OB为半径作圆，交AC于E、F，交AB于D。若E是弧DF的中点，且AE：EF=3：1，FC=4，求ÐCBF的正弦值及BC的长。

十、（本题11分）

29．已知二次函数，它的图象与x轴只有一个交点，交点为A，与y轴交于点B，且AB=2。
　　(1)求二次函数解析式；
　　(2)当b<0时，过A的直线y=x＋m与二次函数的图象交于点C，在线段BC上依次取D、E两点，若，试确定ÐDAE的度数，并简述求解过程。

2005年中考数学模拟试题（2）答案

1．B　　　　　  2．C　　　　　　 3．C　　　　　　　 4．D

5．A　　　　　  6．B　　　　　　 7．B　　　　　　　 8．A

9．C　　　　　  10．A

11．（－4，－3）　　　　　　　　 12．60

13．20　　　　　　　　　　　　  14．五

15．15p　　　　　　　　　　　　 16。

17．　　　　　  　　　　　 18。=-1

19．－2<x<1 　　　　　　　　　　20．DDCE≌DBAF

21．2　　　　　　　　　　　　　 22．x=－9，x=1

23．设甲组单独完成此项工程需要x天，则乙组单独完成此顶工程需要（x＋2）天。依题意，得：，整理得：解得：，经检验x=10，x=－1都是原方程的根，但x=－1不合题意，舍去。当x=10时，x＋2=12。答：单独完成此项工程甲组需要10天，乙组需要12天。

24．一次函数和反比例函数的解析式分别为。矩形ABCD中，AD=BC=7，AB=DC=4，ÐC=90°　　∵ÐRPC=45°　　\ÐR=45°=ÐRPC　 \PC=RC　　∵BP=x \PC=7－x　　 ∵AD∥BC　　　　\QD=RD=RC－DC=7

25．－x－4=3－x  \AQ=AD－QD=7－(3－x)=4＋x 　　\y=4x＋8　　 当Q与D重合时，PC=DC=4，BP=3　　∵P与B不重合，Q与D不重合　　\自变量x的取值范围是0<x<3

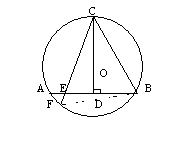26．如图：

连结FB　  ∵CD过圆心O，且CD⊥AB　  ∴CA=CB　　∴∠CBE=∠F　　∵∠BCE公用　　∴DCBE∽DCFB　　 　　　

27．(1)当k=0时，方程(1)化为－x－1=0，x=－1，方程有整数根　　当k≠0时，方程(1)可化为(x＋1)(kx＋k－1)=0　　解得　　∵方程(1)的根是整数，所以k为整数的倒数。∴k是整数 　　　　　∴k=1舍去　　∴k=0，k=－1 (2)当k=0时，方程(2)化为　　∵方程(2)有两个实数根 　　 ，方程有两个实数根　　　  

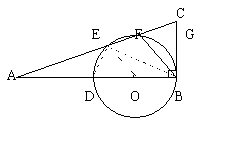28．如图：
解法一：连结OE，DF　  ∵E是DF的中点，BD是⊙O的直径　　∴OE⊥DF，∠DFB=90°　　则可有OE∥BF　　∴AE：EF=AO：OB，且AE：AF=OE：BF　　又∵AE：EF=3：1　　∴AO：OB=3：1，AE=3EF，OE：BF=3：4　　设OB=r，则AO=3r，　　∴AD=2r　　∵AE·AF=AD·AB　　∴3EF·4EF=2r·4r　  　　∵∠ABC=90°(即AB^BC)，DB是⊙O的直径　　\BC是⊙O的切线　　\　　在RtDABC中，由勾股定理，得　　　　　　　　　 　　　 　　　 
解法二：如图：
 连结DE、OE、EB　　由解法一，有　　∵DB是直径　　∴∠DEB=90°　　在RtDDEB中，由勾股定理，有　　　　　　　∵∠CBF=∠CEB，且∠C公用　　∴DCFB∽DCBE　　　　　　　
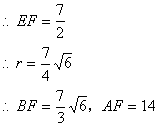　 过F点作FG∥AB，交CB于G
　　
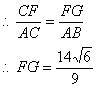
　　在RtDFGB中，由正弦定义，有
　　　　　 

29．解法一：(1)∵的图象与x轴只有一个交点　　∴一元二次方程＝0有两个相等的实数根　　　 　　　　由AB=2，得A与B不重合，又a>0　  ∴c>0　  ∴ac=1　　  ∴二次函数与x轴，y轴交点坐标为　　在RtDABO中，　　　　把(1)代入(2)，解得　　把　　 \二次函数解析式为
(2)当b<0时，由二次函数的解析式　　　　 直线与二次函数图象交点C的坐标为　　过C点作CF^x轴，垂足为F，可推得　　AB=AC，ÐBAC=90°(如图所示)

　　在CF上截取CM=BD，连结EM、AM，则
　　 可证DABD≌DACM　　从而可证DDAE≌DMAE　　 ∴∠1=∠2，∠DAE=∠EAM　　∴∠DAM=∠BAC=90°　　∴∠DAE=45°