中考选择题的常用解法
数学选择题通常为单项选择题。解答选择题的常用方法有
(1) 直接法：直接从已知条件出发，通过准确的运算，严密的推理，得出正确的答案， A.－17 ；B.－7 ； C. 7 ； D.－3
例2 将二次三项式
x2 – 2x+1进行配方，正确的结果是（ ）。
（A）（x+2）2 – 1 （B） （x+2）2+1
（C）（x – 2）2 – 1 （D）（x – 2）2+1
(2)特殊值法特殊值法是恰当地选取适合已知条件的某些特殊值进行验算，得出正确判断的选择方法。
（一）特殊值法在因式分解中的应用
①把多项式 2a(a+1)2+a4-a2+1分解因式正确答案是（ ）
(A) (a2+a-1)2 (B) (a2-a+1)2 (C) (a2+a+1)2 (D) (a2-a-1)2
②把多项式 x2y-y2z+z2x-x2z+y2x+z2y-2xyz 因式分解后的结果是（ ）
(A) （y-z）(x+y)(x-z) (B) (y-z)(x-y)(x+z)
(C) (y+z)(x-y)(x+z) (D) (y+z)(x+y)(x-z)
练习：（1）把多项式 a4-3a2+1 正确答案是（ ）(A) (a2+a+1)(a2-a+1)
(B) (a2-a+1)(a2-a-1) (C) (a2+a+1)(a2-a-1) (D) (a2+a-1)(a2-a-1)
(2) 在 实数范围内，分解因式 4x2--4x--1 等于（ ）
(A)（x --
）(x-- 
) (B) 4(x-- 
)(x-- 
)
（C）
(2x+1--
) (2x+1+ )
(D) (2x--1- )(2x--1 + )
(二)特殊值法在根式中的应用
（1）如果2
--1= 
,x 的值是（ ）（A）
(B) 3 (C) 4 (D) 9
（２）若 0﹤x ﹤1
, 则x2, x, , 
这四个数中（ ）
（A） 最大x2 最小 （B）x 最大 最小
（C）x2最大 , 最小
（D）x
最大x2 最小
（三）特殊值法在方程中的应用
（1）实数x,y,z满足x+y=5, z2 =xy+y--9 则x+2y+3z的值为（ ）
(A). 6 (B). 7 (C) . 8 (D). 9
（2）若点（
都是反比例函数y=
图像上的点，并且
，则下列式子正确的是（
）
（A）
(四).特殊值法在不等式中的应用
⑴．如果 0>x>y ,那么 x2 , xy , y2之间的关系是（ ）
（Ａ） x2 < xy < y2 （B） x2 >xy> y2
(C) x2 >y2 > xy (D) xy <x2 <y2
⑵．如果a<0 , a+b>0,把 a ,--a , b , --b 用“>”连结应是（ ）
（A） a>－a>b>--b (B) b>－b>--a>a
(C) b>－a>a>--b (D) －a>a>b>－b
(五).特殊值法在乘方中的应用
计算 (--2)2n+1+2 (--2)2n 其结果是（ ）
（Ａ）２2n+1 (B) -２2n+1 (C) 0 ( D) 1
⒈化简：(a+b－c)(c－a－b)(a--c--b)4(c+b－a)2正确的是（ ）
（A）－(a+b－c)2(c+b－a)6 (B) (a+b－c)2(a－b－c)2
(C) (－a+b+c)8 (D) －(a+b+c)8
⒉任意两个奇数的平方差必是（ ）
（Ａ）３的倍数 （Ｂ）５的倍数 （C）8 的倍数 （D）以上都不对
⒊若a－c=－2 ,c－b= －3 ,则代数式 (a－b)[(a－c)2－(a－c)(c－b)+(c－b)2]值是（ ）
（A） －8 (B) 27 (C) 19 (D) －35
六)特殊值法是恰当地选取适合已知条件的某些特殊值进行验算，得出正确判断的选择方法。
例1 若x ＜－2，那么│1－│1＋x││的值是（ ）。
（A）―2―x； （B）―2＋x； （C）2－x； （D）x＋4。
（1） 淘汰法淘汰法是利用已知条件和供选答案所提供的“信息”，逐个地淘汰掉所有错误的答案，最后得到正确答案的选择方法。
例1 已知：（a – 3）2+│b - 4│=0，那么
的平方根是（ ）。
（A）
（B）
；（C）
；（D）
。
例2下列方程有实数解的是（ ）。（A）
（B）
（C）
，
（D）
。
例3、下列计算中，正确的是（ ）
A）
B）
C）
D）
= 
（苏州1999）
例4、下列计算正确的是（ ）（苏州2000）
A）
B）
C）
D）
（4）检验法检验法是将所有答案逐个检验，从中确定正确答案的选择方法。
例1
下列各组值中，是方程组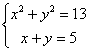
的解的是（ ）。（A）
；（B）
； （C）
； （D）
。
例2 方程2x（x – 3）=5（x – 3）的根是（ ）。（A）x=
；（B）x=3；（C）x1=3，x2=；（D）x= －
。
例3 不等式组
的解集是 （
）A）x>3 B)x< --2 C)—2<x<3 D)—3<x<2(苏州2000)
练习：选择题（每小题只有一个正确答案）
1、珠穆朗玛峰海拔高度848m，吐鲁番盆地海拔高度－155m， 珠穆朗玛峰峰顶比吐鲁番盆地盆底高（ ）。（A）9003m；（B）8693m；（C）―8693m；（D）―9003m。
2、我国幅员辽阔，南北相距约5500km，用科学记数法表示为（ ）。
（A）55×102km；（B）5.5×103km；（C）5.5×104km：（D）0.55×104km。
3、我国的国土面积约为9.60×106km2，由四舍五入得到的近似数9.60×106（ ）。
（A）有3个有效数字，精确到百分位；（B）有3个有效数字，精确到百万位；
（C）有3个有效数字，精确到万位；（D）有2个有效数字，精确到十万位。
4、下列方程中有实数根的是（ ）
（A）
= 0（B）
（C）x2-2x+2=0 （D）
5、下列计算中，正确的是（ ）
A a2+2a2=3a4 B 2x3·(―x2)=2x5
C (―2a2)3=8a5 D 6x2m÷2xm=3x2
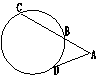6、如图，AC交⊙O于点B、C，AD切⊙O于点D，已知BC=6，AB=2，
则AD的长为（ ）
A
12 B 16 C 2
D 4
7. 在下列图形中，既是中心对称图形又是轴对称图形的是（ ） 6题图
A. 等腰三角形 B. 圆 C. 梯形 D. 平行四边形
8、已知两个圆只有一条公切线，那么这两个圆的位置关系是（ ）
A. 内切 B. 外切 C. 相交 D. 外离
9、下列命题正确的是（ ）。
（A）顶点在圆周上的角叫做圆周角。（B）圆内接平行四边形一定是矩形。
（C）平分弦的直径一定垂直于弦。（D）与直径垂直的直线是圆的切线。
阅读理解题
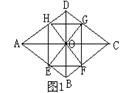例题1、以下是一道题目及其解答过程。已知：如图1、从菱形ABCD的对角线的交点O分别向各边引垂线，垂足分别是E、F、G、H。求证：四边形EFGH是矩形。
证明：∵四边形ABCD是菱形，∴AO=CO，∠AOD=∠COD=900①
又∵DO=DO∴ΔAOD≌ΔCOD。∵OH、OG分别是RtΔAOD和RtΔCOD斜边上的高，∴OH=OG，③同理OH=OE，OE=OF，则OH=OE=OF=OG。∴EG与HF相等且互相平分。
∴四边形EFGH是矩形。④以上证明过程中（ ）
A、①到②有错误 B、②到③有错误 C、③到有④错误 D、没有错误
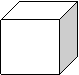
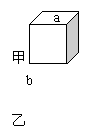例题2、阅读下面的短文，并解答问题。我们把相似形的概念推广到空间：如果两个几何体大小不一定相等，但形状完全相同，就把它们叫做相似体。如图3、甲、乙是两个不同的正方体。正方体都是相似体，它们的一切对应线段之比都等于相似比（a：b）。设S甲、S乙分别表示这两个不同的正方体的表面积，则
。
又设V甲、V乙分别表示这两个正方体的体积，则
（1）下列几何体中，一定属于相似体的是（ ）
A、两个球体 B、两个圆锥体 C、两个圆柱体 D、两个长方体
（2）请归纳出相似体的三条主要性质：①相似体的一切对应线段（或弧）长的比等于 ②相似体表面积的比等于 ；③相似体体积的比等于 ；
（3）假定在完全正常发育的条件下，不同时期的同一人是相似体。一个小朋友上幼儿园时身高为1.1米，体重为18千克，到了初三时，身高为1.65米。问他的体重是多少？
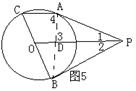例题3、请阅读下题及证明过程，并回答所提出的问题。如图5、已知P为⊙O外一点，A和B是切点，BC为直径。求证：AC∥OP。
证明：连结AB，交OP于点D。∵PA、PB切圆O于A、B，∴PA=PB，∠1=∠2。∴PD⊥AB。∴∠3=900。∴ ，（*）∴∠4=900。∴∠3=∠4。∴AC∥OP
（1） 在（*）处的横线上补充的条件；
（2） 上述证明过程中用到的定理名称或定理的具体内容（只要求写出两个）
① ；② ；
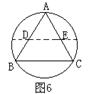
例题6、（1）如图6、把正三角形ABC的外接圆对折，使点A落在弧BC的中点。如果BC=5，那么折痕在ΔABC内的部分DE的长为 ；
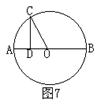
（2）如图7、AB是⊙O的直径，CD⊥AB，设∠COD=α，那么
的值为
；
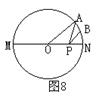
（3）如图8、A点是半圆上一个三等分点，点B是弧AN的中点，P点是直径MN上的一个动点，⊙O的半径为1，那么AP+BP的最小值为 ；
