二 次 函 数
1、已知：二次函数y=x2-kx+k+4的图象与y轴交于点c，且与x轴的正半轴交于A、B两点（点A在点B左侧）。若A、B两点的横坐标为整数。
（1）确定这个二次函数的解析式并求它的顶点坐标；（2）若点D的坐标是(0,6），点P（t,0)是线段AB上的一个动点，它可与点A重合，但不与点B重合。设四边形PBCD的面积为S，求S与t的函数关系式；
（3）若点P与点A重合，得到四边形ABCD，以四边形ABCD的一边为边，画一个三角形，使它的面积等于四边形ABCD的面积，并注明三角形高线的长。再利用“等底等高的三角形面积相等”的知识，画一个三角形，使它的面积等于四边形ABCD的面积（画示意图，不写计算和证明过程）。
2、（1）已知：关于x、y的方程组 有两个实数解，求m的取值范围；
(2）在（1）的条件下，若抛物线y=-(m-1)x2+(m-5)x+6与x轴交于A、B两点，与y轴交于点C，且△ABC的面积等于12，确定此抛物线及直线y=(m+1)x-2的解析式；
（3）你能将（2）中所得的抛物线平移，使其顶点在（2）中所得的直线上吗？请写出一种平移方法。
3、已知：二次函数y=x2-2(m-1)x+m2-2m-3，其中m为实数。
（1）求证：不论m取何实数，这个二次函数的图像与x轴必有两个交点；（2）设这个二次函数的图像与x轴交于点A(x1,0)、B(x2,0),且x1、x2的倒数和为 ,求这个二次函数的解析式。
4、已知二次函数y1=x2-2x-3. (1)结合函数y1的图像，确定当x取什么值时，y1>0,y1=0,y1<0;
(2)根据（1）的结论，确定函数y2= (y1-y1)关于x的解析式；
（3）若一次函数y=kx+b(k 
0)的图像与函数y2的图像交于三个不同的点，试确定实数k与b应满足的条件。
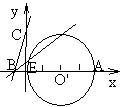
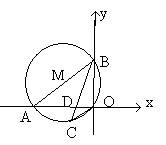5、已知：如图，直线y= x+ 
与x轴、y轴分别交于A、B两点，⊙M经过原点O及A、B两点。
（1）求以OA、OB两线段长为根的一元二次方程；
（2）C是⊙M上一点，连结BC交OA于点D，若∠COD=∠CBO,
写出经过O、C、A三点的二次函数的解析式；
（3）若延长BC到E，使DE=2,连结EA，试判断直线EA与
⊙M的位置关系，并说明理由。（河南省）
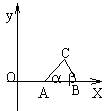6、如图，已知点A（tan ,0） B(tan ,0)在x轴正半轴上，点A在点B的左
边， 、 是以线段AB为斜边、顶点C在x轴上方的Rt△ABC的两个锐角。
（1）若二次函数y=-x2- 5/2kx+(2+2k-k2)的图像经过A、B两点，求它的解析式；
（2）点C在（1）中求出的二次函数的图像上吗？请说明理由。（陕西省）
7、已知抛物线y=x2和直线y=(m2-1)x+m2.
（1）当m为何实数时，抛物线与直线有两个交点？
（2）设坐标原点为O，抛物线与直线的交点从左至右分别为A、B，
当直线与抛物线两点的横坐标之差为3时，求△AOB中的OB
边上的高。（四川省）
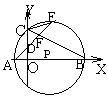
8、如图，P为x轴正半轴上一点，圆P交x轴于A、B两点，
交y轴于C点。弦AE分别交OC、CB于D、F。已知 = 。
（1）求证：AD=CD；
（2）若DF＝5/4 ，tan∠ECB=3/4 ,求经过A、B、C三点的抛物线的解析式；
（3）设M为x轴负半轴上一点，OM= AE，是否存在过点M的直线，
使该直线与（2）中所得的抛物线的两个交点到y轴距离相等？若存在，
求出这条直线的解析式；若不存在，请说明理由。（大连市）
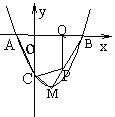
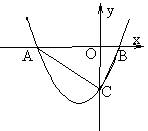
9、如图，抛物线y=ax2+bx+c与x轴交于A、B两点（点A在点B左侧），
与y轴交于点C，且当x=0和x=2时，y的值相等．直线y=3x-7与这条抛物线
相交于两点，其中一点的横坐标是4，另一点是这条抛物线的顶点M．
（1）求这条抛物线的解析式；
（2）P为线段BM上一点，过点P向x轴引垂线，垂足为Q．若点P在线段
BM上运动（点P不与点B、M重合），设OQ的长为t,四边形PQAC的面积为S．
求s与t之间的函数关系式及自变量t的取值范围； （3）在线BM上是否存在点N，使△NMC为等腰三角形？若存在，请求出点N的坐标；若不存在，请说明理由．(哈尔滨市）
10、如图，在直角坐标系中，点O'的坐标 为（2，0），⊙O'与x轴交于原点O和点A，B、C、E三点的坐标分别为（-1，0），（0，3）和（0，p)且0＜p≤3.
(1)求经过点B、C的直线的解析式；
（2）当点E在线段OC上移动时，直线BE与⊙O'是这几种位置关系？
当P分别在什么范围内取值时，直线BE与⊙O'是这几种位置关系？
（3）设过点A、B、E的抛物线的顶点是D，求四边形ABED的面积的最大或最小值．
11、已知：抛物线y=a(x-t-1)2+t2(a,t是常数，a≠0,t≠0)的顶点是A，抛物线y=x2-2x+1的顶点是B．
（1）判断点A是否在抛物线y=x2-2x+1上，为什么？
（2）如果抛物线y=a(x-t-1)2+t2 经过点B，①求a的值；
②这条抛物线与x轴的两个交点和它的顶点A能否构成直角三角形？
若能，求出t的值；若否不能，请说明理由．（南京市）
12、已知：如图，抛物线c1经过A、B、C三点，顶点为D，
且与X轴的另一个交点为E.
（1）求抛物线C1解析式；（2）求四边形ABDE的面积；
（3）设抛物线C1的对称轴与X轴交于点F，另一条抛物线C2
经过点E(抛物线C2与抛物线C1不重合），且顶点为M(a,b)，对
称轴与X轴相交于点G，且以M,G,E为顶点的三角形与以D,E,F
为顶点的三角形全等，求a,b的值（只需写出结果，不必写出解答过程）．
13、已知：如图，抛物线y=ax2+bx+c(a≠0)经过x轴上的两点
A(x1,0)、B(x2,0)和y轴上的点C（0，-3/2 ），⊙P的圆心P在y
轴上，且经过B、C两点，若b= a,AB=2
.(1)求抛物线的解析式；
（2）D在抛物线上，且C、D两点交于抛物线的对称轴对称，
问直线BD是否经过圆心P？并说明理由；
（3）设直线BD交⊙P于另一点E，求经过点E 的⊙P的切线的解析式．
14、已知二次函数y=x2+ax+a-2．
（1）求证：不论a取何值时，抛物线y=x2+ax+a-2的顶点Q总在x轴的下方；
（2）设抛物线y=x2+ax+a-2与y轴交于点C，如果过点C且平行于x轴的直线与抛物线有两个不同的交点，并设另一个交点为点D，问：△QCD能否是等边三角形？若能，请求出相应的二次函数解析式；若不能，请说明理由；（3）在第（2）题的已知条件下，又设抛物线与x轴的交点之一为点A，则能使△ACD的面积等于1/4的抛物线有几条？请证明你的结论．（杭州市）
15、已知开口向上的抛物线y=ax2+bx+c(a≠0)与x轴交于A(x1,0)、B(x2,0)
两点，x和x是方程x2+2x-3=0的两个根（ｘ1＜ｘ2）而且抛物线与y轴交于
C点，∠ACB不小于90°．
（1）求点A、点B的坐标和抛物线的对称轴；
（2）求点C的坐标（用含a的代数式表示）；（3）求系数a的取值范围．
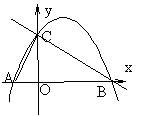
16、已知：如图，直线y=-x+3与x轴、y轴分别交于点B、C，抛物线
y=-x+bx+c经过点B、C,点A是抛物线与x轴的另一个交点．（深圳市）
（1）求抛物线的解析式；
（2）若点P在直线BC上，且S△PAC=1/2S△PAB,求点P的坐标．