2002年全国中考试题选
 1.(北京)已知:AB为⊙O的直径,P为AB延长线上的一个动点,过点P作⊙O的切线,设切点P作⊙O的切线,设切点为C.
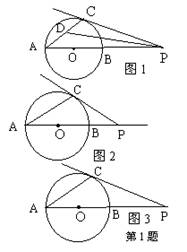
1.(北京)已知:AB为⊙O的直径,P为AB延长线上的一个动点,过点P作⊙O的切线,设切点P作⊙O的切线,设切点为C.
(1)当点P在AB延长线上的位置如图1所示时,连结AC,作
∠APC的平分线,交AC于点D,请你测量出∠CDP的度数;
(2)当点P在AB延长线上的位置如图2和图3所示时,连
结AC,请你分别在这两个图中用尺规作∠APC的平分线
(不写作法,保留作图痕迹),设此角平分线交AC于点D,
然后在这两个图中分别测量出∠CDP的度数.猜想:
∠CDP的度数是否随点P在AB延长线上的位置的变
化而变化?请对你的猜想加以证明.
2.(辽宁)已知:如图,P与x轴相交于坐标原点O,点A(0,2)
是P与y轴的交点,点B(-2![]() ,0)在x轴上,连结BP交P于
,0)在x轴上,连结BP交P于
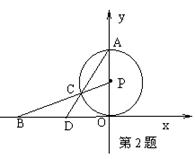 点C,连结AC并延长交x轴于点D.
点C,连结AC并延长交x轴于点D.
(1)求线段BC的长;(2)求直线AC的函数解析式;
(3)当点B在x轴上移动时,是否存在点B,使△BOP相
似于△AOD?若存在,求出符合条件的坐标;若不存在,说明理由.
3.(甘肃)如图;在△ABC 中,AB=4,BC=3,∠B=90°,
点D在AB上运动,但与A、B不重合,过B、C、D
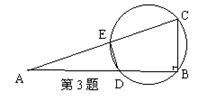 三点的圆交AC于E ,连结DE.(1)设AD=x,CE=y,求y与x之间的
三点的圆交AC于E ,连结DE.(1)设AD=x,CE=y,求y与x之间的
函数关系式,并指出自变量x的取值范围;
(2)当AD长为关于x的方程2x2+(4m+1)x+2m=0的一个
整数根时,求m的值.
 4.(甘肃)如图,在直角坐标系xoy中,以点A(0,-3)为圆心
4.(甘肃)如图,在直角坐标系xoy中,以点A(0,-3)为圆心
作圆与x轴相切,⊙B与⊙A外切于点P,B点在x轴正半轴上,
过P点作两圆 的公切线DP交y轴于D,交x轴于C
.(1)设⊙A的半径为r1,⊙B的半径为r2,且r2=![]() r1,求公切线
r1,求公切线
DP的长及直线DP的函数解析式;(2)若⊙A的位置,大小不变,
点B在x轴正半轴上移动,⊙B与⊙A始终外切,过D作⊙B
的切线DE ,E为切点,当DE=4时,B点在什么位置?从解答中能发现什么?
 5.(哈尔滨)如图,△ABC内接于O,BC=4,S△ABC=6
5.(哈尔滨)如图,△ABC内接于O,BC=4,S△ABC=6![]() ,∠B为
,∠B为
锐角,且关于x的方程x2-4cosB+1=0有两个相等的实数根.D是
劣弧AC上任一点(点D不与点A、C重合),DE平分∠ADC,
交O于点E,交AC 于点F.(1)求∠B的度数;(2)求CE的长;
(3)求证:DA、DC的长是方程y2-DE·y+DE·DF=0的两个实数根.
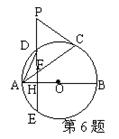 6.(济南)如图,AB、AC分别是⊙O的直径和弦,D为劣弧AC上一点,
6.(济南)如图,AB、AC分别是⊙O的直径和弦,D为劣弧AC上一点,
交O于点E,交AC于点F,P为ED的延长线上一点。
(1)当△PCF满足什么条件时,PC与⊙O相切,为什么?
(2)当点D在劣弧AC的什么位置时,才能使AD2=DE·DF,为什么?
7 .(青岛)已知:如图△ABC内接于O ,AB=AC,AO⊥BC于D。
(1)求证:△ABC是等边三角形;
(2)若AB=1,P是劣弧BC上的一个动点(点P与B、C不重合),
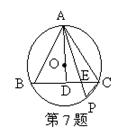 PA交BC于点E,设AE=x,EP=y,求y与x之间的函数关系式,
PA交BC于点E,设AE=x,EP=y,求y与x之间的函数关系式,
并写出自变量x的取值范围;
(3)在(2)的前提下,令∠PAC=α,∠APC=β,
当y取何值时,sin2α+sin2β=1.
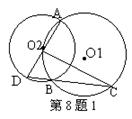
8.(呼和浩特)已知⊙O1与⊙O2相交于A、B两点,
且点O2在⊙O1上。(1)如图1,AD是⊙O2的直径,
连结DB并延长交⊙O1于C,求证:CO2⊥AD.
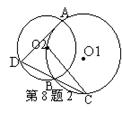 (2)如图2,如果AD是⊙O2的一条弦,连结DB并延长
(2)如图2,如果AD是⊙O2的一条弦,连结DB并延长
交⊙O1于C,那么CO所在直线是否与AD垂直?证明你的结论。
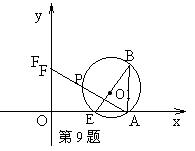
9.(武汉)如图,已知:在直角坐标系中,点E从O点出发,以1个
单位/秒的速度沿x轴正方向运动,点F从O点出发,以2个单位/秒
的速度沿y 轴正方向运动。B(4,2)、以BE为直径作⊙O1。
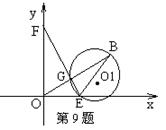 (1)若点E、F同时出发。设线段EF与线段OB交于点G,试判断点
(1)若点E、F同时出发。设线段EF与线段OB交于点G,试判断点
G与⊙O1的位置关系,并证明你的结论;
(2)在(1)的条件下,连结FB、几秒时FB与⊙O1相切?
(3)若点E提前2秒出发,点F再出发。当点F出发后,
E点在A点左侧时,设BA⊥x轴于A点。连结AF交⊙O1于
点P,试问APAF的值是否会发生变化?若不变,请说明理由,
并求其值;若变化,请求其值的变化范围。
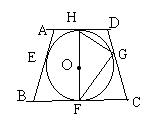
 10.(深圳)如图,等腰梯形ABCD中,AD∥BC,AB=CD,以HF
10.(深圳)如图,等腰梯形ABCD中,AD∥BC,AB=CD,以HF
为直径的⊙O与AB、BC、CD、DA相切,切点分别是E、F、G、
H.其中H为AD的中点,F为BC的中点。连结HG、GF。
(1)若HG和GF的长是关于x的方程x2-6x+k=0的两个实数根,
求⊙O的直径HF(用含k的代数式表示),并求出k的取值范围。
(2)如图,连结EG、DF。EG与HF交于点M,与DF交于点N,
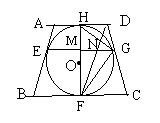 求
求![]() 的值。
的值。
![]()