福建省泉州市2004年数学中考试题
一、填空题:(每小题3分,共36分)
1、-1的相反数是 ;
2、分解因式:x2-4= ;
3、某种药品原来的价格100元,现按原价的80℅出售,则该药品现在的价格是 元;
 4、一个地区1月份某周各天的最低气温依次是(单位:℃) 3,1,1,-1,1,-2,-3。则它们的平均温度是
℃;
4、一个地区1月份某周各天的最低气温依次是(单位:℃) 3,1,1,-1,1,-2,-3。则它们的平均温度是
℃;
5、函数![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
6、如图,DE是△ABC的中位线,BC=8,则DE= ;
 7、已知:⊙O1与⊙O2相外切,O1O2=7,⊙O1的半径为,则⊙O2的半径为
;
7、已知:⊙O1与⊙O2相外切,O1O2=7,⊙O1的半径为,则⊙O2的半径为
;
8、对于一次函数y=2x+1,y随着x的增大而 ;
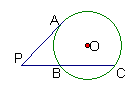
9、如图,PA与⊙O相切于点A,PBC为割线,PA=4,PC=8,则PB= ;
10、一个圆柱形的保温杯底面半径为3㎝,高为16㎝,则保温杯的
侧面积为 ;
 11、一定质量的二氧化碳,它的密度
11、一定质量的二氧化碳,它的密度![]() (kg/m3) 是它体积V(m3)的反比例函数,当V=5m3时,
(kg/m3) 是它体积V(m3)的反比例函数,当V=5m3时,![]() =1.98kg/m3;则当V=10m3时,
=1.98kg/m3;则当V=10m3时,![]() =
kg/m3;
=
kg/m3;
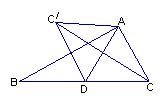
12、如图,AD是Rt△ABC斜边上的中线,把△ADC沿AD对折,
点C落在点C/处,连结CC/,则图中共有等腰三角形 个。
二、选择题(每小题4分,共24分)
13、计算(a2)3的结果应是( )
A、a5 B、a6 C、a8 D、a9
14、地球到太阳的距离约为千米,用科学记数法表示应约为( )
A、1.5×108千米 B、1.5×107千米 C、0.15×108千米 D、15×107千米
15、不等式组![]() 的解集情况为(
)
的解集情况为(
)
A、x<5 B、x>1 C、1<x<5 D、无解
16、一元二次方程x2-3x+1=0的两根为x1、x2,则x1·x2的值为( )
A、1 B、-1 C、3 D、-3
17、若限于用同一种正多边形磁砖镶嵌(要求镶嵌的正多边形的边必须与另一正多边形的边重合),则不能镶嵌成一个平面的正多边形磁砖的形状是( )
A、正三角形 B、正方形 C、正六边行 D、正八边行
18、我们来探究 “雪花曲线”的有关问题:下图(3)是边长为1的正三角形,将此正三角形的每条边三等分,而以居中的那一条线段为底边再作正三角形,然后以其两腰代替底边,得到第二个图形如下图(4);再将下图(2)的每条边三等分,并重复上述的作法,得到第三个图形如下图(5),如此继续下去,得到的第五个图形的周长应等于( )
 A、3 B、
A、3 B、![]()
C、![]() D、
D、![]()
三、解答题(共90分)
19、(8分)计算:(-2)3+-7-30
20、(8分)先化简下面的代数式,再求值:(x+1)2-2(x+2), 其中![]()
 21、(8分)用换元法解方程:
21、(8分)用换元法解方程:![]()
22、(8分)如图,已知:AB=CD,DE⊥AC,BF⊥AC,垂足分别为E、F,
∠B=∠D,求证:AF=CE
23、(8分)如图,拦水坝的横断面是梯形ABCD,坡角α=28º,斜坡AB=9米,求拦水坝的高BE
 (精确到0.1米,供选用的数据:sin28º=0.4695,cos28º=0.8829,
(精确到0.1米,供选用的数据:sin28º=0.4695,cos28º=0.8829,
tan28º=0.5317,cot28º=1.8807)
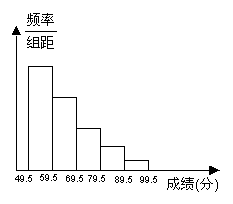 24、(8分)在某中学举行的环保知识竞赛中,将参赛学生成绩进行整理后分成五组,绘制成频率直方图(如图).已知图中从左到右的第一、二、三、四、五小组频率分别为0.4、0.3、0.15、0.1、0.05,第一小组的频数是20.
24、(8分)在某中学举行的环保知识竞赛中,将参赛学生成绩进行整理后分成五组,绘制成频率直方图(如图).已知图中从左到右的第一、二、三、四、五小组频率分别为0.4、0.3、0.15、0.1、0.05,第一小组的频数是20.
(1)求参赛学生的人数;
(2)参赛学生成绩的中位数应落在
哪一分数段内?(不必说明理由)?
25、(8分)如图,⊙O为四边形ABCD的外接圆,圆心O在AD上,OC∥AB.
(1)求证:AC平分∠DAB
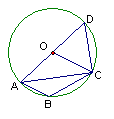 (2)若AC=8,AD:BC=5:3,试求⊙O的半径。
(2)若AC=8,AD:BC=5:3,试求⊙O的半径。
26、(8分)某施工队修建一个抛物线形的水泥门洞,其高度OM为8米,地面宽度AB为12米,在门洞中搭一个“三角架”CDE.使C点在门洞的左侧,D为OB的中点,CE⊥AB于E,以AB所在直线为x轴,AB的中点O为原点建立直角坐标系(如图所示)
 (1)请你直接写出A、B、M三点的坐标;
(1)请你直接写出A、B、M三点的坐标;
(2)现测得DE=7米,求“三角架”的高CE。
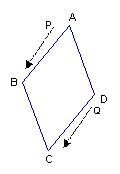
27、(13分)如图,菱形ABCD的边长为24厘米,∠A=60°,质点P从点A出发沿着AB-BD作匀速运动,质点Q从点D同时出发沿着线路DC—CB—BA作匀速运动。
(1)求BD的长;
(2)已知质点P、Q运动的速度分别为4㎝/秒、5㎝/秒,经过12秒后, P、Q分别到达M、N两点,若按角的大小进行分类,请问△AMN是哪一类三角形,并说明理由;
(3)设问题(2)中的质点P、Q分别从M、N同时沿原路返回,质点P的速度不变,质点Q的速度改变为a㎝/秒,经过3秒后, P、Q分别到达E、F两点,若△BEF与题(2)中的△AMN相似,试求a的值。
 |
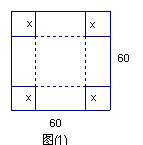
28、(13分)用一块边长为60㎝的正方形薄钢片制作一个长方体盒子:
(1)如果要做成一个没有盖的长方体盒子,可先在薄钢片的四个角上截去四个相同的小正方形(如图1),然后把四边折合起来(如图2)。
①求做成的盒子底面积y(㎝2)与截去小正方形边长x(㎝)之间的函数关系式;
②当做成的盒子的底面积为900㎝2时,试求该盒子的容积。
(2)如果要做成一个有盖的长方体盒子,起制作方案要求同时符合下列两个条件:
①必须在薄钢片的四个角上各截去一个四边形(其余部分不能裁截)
②折合后薄钢片既无空隙又不重叠地围成各盒面。
请你画出符合上述制作方案的一种草图(不必说明画法与根据);并求当底面积为
800㎝2时,该盒子的高。
 | |||
 | |||