2005年数学中考模拟试题

一、选择题（每小题3分，共30分）

1．对有理数230800精确到万位，用科学计数法表示为

A.　23；　　B.　2.3×10⁵ ；　 C.　2.31×10⁵ ；　 D.　2.30×10⁵

2．已知x₁，x₂是方程2x²+3x=1的两个根，则+的值是
A.　3　　　  B.　-3　　　  C.　　　　　D.　 －

3．给出下面四个命题：(1)一组对边平行的四边形是梯形;(2)一条对角线平分一个内角的平行四边形是菱形;(3)两条对角线互相垂直的矩形是正方形;(4)圆的切线垂直于半径,其中真命题的个数有

A．0个　　 B.　1个　　 C.　2个　　　　D .　3个

4．随着通讯市场竞争日趋激烈,某通讯公司的手机市话收费标准按原标准每分钟降低了元后，再次下调25％.现在的收费标准是每分钟元，则原收费标准每分钟为

　 　A.元　 B. 元　　C. 元　　D. 元

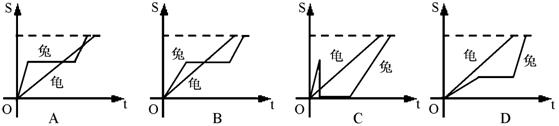
5. 龟兔赛跑，它们从同一地点同时出发，不久兔子就把乌龟远远地甩在后面，于是兔子便得意洋洋地躺在一棵大树下睡起觉来.乌龟一直在坚持不懈、持之以恒地向终点跑着，兔子一觉醒来，看见乌龟快接近终点了，这才慌忙追赶上去，但最终输给了乌龟.下列图象中能大致反映龟兔行走的路程S随时间t变化情况的是

6．半径为1cm的两个等圆，其中一圆经过另一个圆的圆心，那么这两圆的公共弦长为

A.　3cm　　 B.　2cm　　　C.　cm　　　D.　

7．关于的方程有实数根，则的取值范围是

A.　 　　B. . ≥－4　C. ≥－4且≠0  D.≤－4

8．已知：ABCD是正方形，E是CD的中点，P是BC边上的一点，下列条件中，不能推出△ABP与△ECP相似的是

A.∠APB=∠EPC　 B. ∠APE=90⁰　C. P是BC的中点　 D.　BP：BC=2：3

9． 二次函数y=－x²+2（m－1）x+2m－m²的图象关于y轴对称,顶点A和它与x轴的两个交点B、C所构成的△ABC的面积为

A .　1　　　  B.　2　　　　  C.　　　　　　　　D.　　

10． 两圆的半径恰好是方程x^２－4x+1=0的两个根，当这两圆相交时，圆心距d的取值范围是

A . d<4　　B.　1<d<4　　C.　　2<d<4　　D.　　d>2

二、填空题（每题3分，共24分）

11.当b<0时,化简a+b=　　　　　　 .

12.　若不等式组的解集是-1<x<1,那么(a+1)(b-1)的值等于　　　　 

13．抛物线的对称轴是　　　　　 .

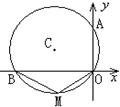
14.如图，⊙C经过原点且与两坐标轴分别交于点A与点B，点A的坐标为（0，4），M是圆上一点，∠BMO=120º，圆心C的坐标是　　　　  . 

15．如图，菱形ABCD的对角线的长分别为2和5，P是对角线AC上任一点（点P不与点A、C重合），且PE∥BC交AB于E，PF∥CD交AD于F，则阴影部分的面积是______.

16.　弦AB把⊙O分成的两条弧的度数比是1：2，则弦AB所对的圆周角是　　　　 

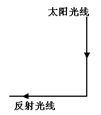
17.如图，一束光竖直照射在一平面镜上，如果要让反射光成水平光线，请在图中画出平面镜的位置，平面镜的镜面与入射光线的夹角应为　　  度。

18.观察下面的点阵图，按照其中的规律摆下去。摆第n个这样的“小屋子”需要的总点数为　　　.

三．解答题：(共7小题66分)

19．（本题6分）先化简，后求值：（－）·，其中ｍ＝，n=.

20. （本题8分）甲、乙两班举行电脑汉字输入速度比赛，各选10名学生参加，各参赛学生每分钟输入汉字个数如下表：

输入汉字（个）	132	133	134	135	136	137	众数	中位数	平均数（）	方差（s2）
甲般学生（人）	1	0	1	5	2	1	135	135	135	1.6
乙班学生（人）	0	1	4	1	2	2

请你填写上表中乙班学生的相关数据，再根据所学的知识，从不同方面评价甲、乙两班学生的比赛成绩（至少从三个不同方面评价）。

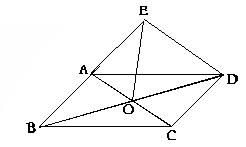
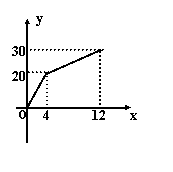21、（本题8分）如图，平行四边形ABCD纸片中，，AC⊥AB，AC与BD交于点O，沿对角线AC对折后，E与B对应.

（1）试问：四边形ACDE是什么形状的四边形？

（2）若EO平分∠AOD成立，其他条件不变还应具备一个什么条件？说明其理由.

22.有一个附有进出入管的容器，每单位时间内进出的水量都是一定的，设从某时刻开始的4分钟内只进水，不出水，在随后的8分钟内既进水又出水，得到时间x（分）与水量y（升）之间的关系如图所示.

（1）4≤x≤12时，x与y有何关系？

（2）若12分钟后只放水，不进水，求y与x的函数关系式. 并在下图中画出函数图象.

23.如图，ΔABC内接于⊙O，D是的中点，DE为直径，EM⊥AB于M，EN⊥AC于N.

　（1）求证：EM=EN；

　（2）已知：AB=5cm，AC=3cm，求AN的长.

（3）在（2）的条件下，若DE平分AB，求sin∠DEM的值.

　

24.某商店将进价为100元的某商品按120元的价格出售，可卖出300个；若商店在120元的基础上每涨价1元，就要少卖10个，而每降价1元，就可多卖30个。

(1).求所获利润y (元)与售价x（元）之间的函数关系式；

(2).为获利最大，商店应将价格定为多少元？

(3).为了让利顾客,在利润相同的情况下,请为商店选择正确的出售方式,并求出此时的售价.

25.已知⊙O是锐角△ABC的外接圆, AB=5cm，AC=cm，BC.边上的高AD=3cm.

(1).求△ABC外接圆的半径.

(2).取的中点G,连BG交AD于E,试求BE的长.

(3).若动点M从点D出发在线段DB上来回匀速运动,速度为2cm/秒，动点N同时从点B出发在劣弧BC上匀速运动，到C点停止运动.问是否存在某一时间(最短时间)使△MNB与△ADC相似,若存在，试求出MN·MB的值；若不存在，请说明理由.

参考答案：

一、 BACDB　CBCAC

二、 11、-2ab　　12、-6　　13、 直线x= - 　　14、 (，2)　　　15、　　16、60°或120°　17、 45　　 18、6n-1

三、 19、化简为=

20、表中依次为134、134.5、135、1.8

两班学生的平均成绩相同，但众数和中位数甲班要强，方差又小，说明甲班学生较稳定。

21、（1）矩形  （2）∠ABO=30°或∠AOB=60°

22、（1）（只要写出x与y的等量关系都可以）

　 （2）（12≤x≤20）图象略.

23、（1）连BE、EC、AE

　　（2）AN=1cm

　　 (3) 此时AB为直径. sin∠DEM=

24、（1）当x>120时，­y­₁=-10x²+2500x-150000

　　　　 当100<x<120时，­y­₂=-30x²+6900x-390000

　　 (2)售价定为115元获得最大为6750元.

（3）设­y­₁=­y­_2，求得售价为120元.

　　25、（1）

（2）

（3）存在，此时MN=，BM=BD=4，MN·MB=.