2004年山东临沂中考数学试题

卷I（42分）

一选择题、(3×14=42分)

1.　　　 －2的倒数是（　　）

A：－2　　B：2　　 C：－　　　 D：

2.　　　 下列运算正确的是（　　）

A：·x³=x⁶B：÷x＝x²C：＝ D：

3.函数的自变量x的取值范围是（　 ）

A：x≤　　 B：x＜且x≠0　　 C：x≥　　  D：x≤且x≠0

3.　　　 下列五种图形：①平行四边形 ②矩形 ③菱形 ④正方形　⑤等边三角形。其中既是中心对称图形又是轴对称图形的共有（　）种

A： 2　　 B：3　　C：4　　D：5

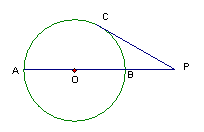5、如图AB是⊙O的直径，P为AB延长线上一点，PC切⊙O于点C，PC=4，PB=2。则⊙O的半径等于（　）

A：1　　B：2　 C：3　 D：4　

6、如果，那么＝（　 ）

A：5　　 B：7　　C：9　　 D：11

7、用换元法解方程时，若设那么原方程化为关于y的方程是（　 ）

A：　 B：　　C：　D：

8、小亮同学的父亲购买了大小相同、颜色不同的两种正五边形的地板砖铺设地面，小亮同学根据所学的知识告诉父亲，这样不能够做到无缝隙、不重复地铺设，那么他们还要购买与正五边形边长相同的（　　 ）砖块

A：正三角形　　  B：正方形　　 C：正六边形　　 D：正十边形

9、若半径分别为2与6的两个圆有公共点，则圆心距d的取值范围是（　 ）

A：d＜8　　B：d≤8　　C：4＜d＜8　　D：4≤d≤8

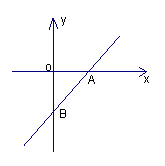10、如图，直线y=kx+b与坐标轴的两个交点分别为A（2，0）和B（0，－3），则不等式kx+b+3≥0的解集是（ ）

A：x≥0　　B：x≤0　 C：x≥2　 D：x≤2

11、点P(x+1, x－1)不可能在第（　）象限

A：一　 B：二　 C：三　 D：四

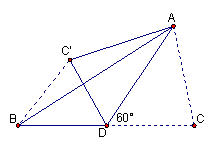
12、如图AD是△ABC的中线，∠ADC=60°，

BC=4，把△ADC沿直线AD折叠后，点C

落在C^’的位置上，那么BC^’为

A：1　 B：　 C：2　　D：

13、若x₁、x₂是关于x的方程x²+bx－3b=0的两个根，且x₁²+x₂²＝7。那么b的值是（　　　）

A：1　　　　 B：－7　　

C：1或－7　　D：7或－1

14、小芳同学在出黑板报时画出了一月牙形的图案

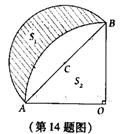如图，其中△AOB为等腰直角三角形，以O为圆心，OA为半径作扇形OAB，再以AB的中点C为圆心，以AB为直径作半圆，则月牙形阴影部分的面积S₁与△AOB的面积S₂之间的大小关系是（　　 ）

A：S₁ ＜S₂　B：S₁ ＝S₂

C：S₁ ＞S₂ D：无法确定

卷ц（非选择题共78分）

二、填空题（15、16、17、18每小题3′，19小题4′）

15、分解因式：m²－4n²―4n―1=　　　　　　　　　　　 .

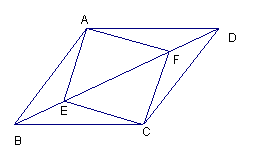16、如图菱形ABCD中，点E、F在对角线BD上，BE=DF=BD，若四边形AECF为正方形，则tan∠ABE=　　　　  。

17、如图某圆柱形的零件，其高为5cm，底面半径

为2cm，为防锈需要涂油漆的面积为　　　　cm²。

18、小明同学在上楼梯时发现：若只有一个台阶

时，有一种走法；若有二个台阶时，可以一阶一

阶地上，或者一步上二个台阶；共有两种走法，

如果他一步只能上一个或者两个台阶，根据上述

规律，有三个台阶时，他有三种走法，那么有四个台阶时，共有　　　　 种走法。

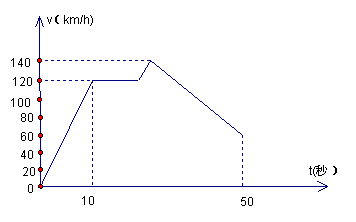19、某新型国产轿车在启动后50秒内时间t（秒）与速度v（km/h）的关系如图所示，则此段时间内，该车的最高时速为　　　　km/h, 从0km/h加速到100km/h至少需要　　　 秒（精确到0.1秒）

三解答题（本大题7小题，共62分）

20、（本题6分）甲、乙两名射击运动员参加某大型运动会的预选赛，在相同的条件下他们分别射靶5次，命中的环数如下表：

甲	9	8	9	9	10
乙	10	10	9	7	9

如果甲、乙两人中只有1人入选，你认为入选者应该是谁？并说明理由。

21、（本小题7分）如图△ABC中，∠B=2∠A, AB=2BC。

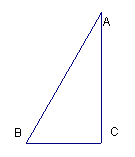求证：∠C=90°

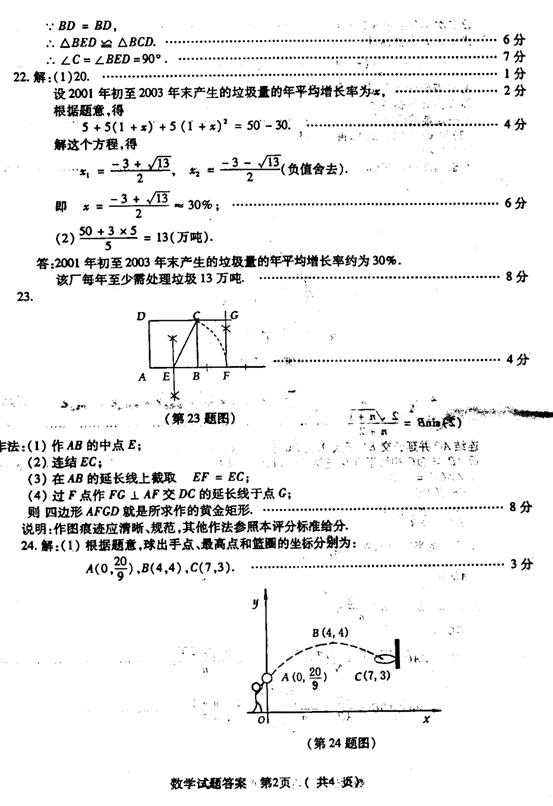
22、（本题满分8分）据某城市的统计资料显示，到2003年末该城市堆积的垃圾已达50万吨，不但侵占了大量土地，而且已成为一个重要的污染源，从2004年起，该城市采取有力措施严格控制垃圾的产生量，但根据预测，每年仍将产生3万吨的新垃圾，垃圾处理已成为该城市建设中的一个重要问题。

（1）若2000年末该城市堆积的垃圾为30万吨，则2001年初至2003年末产生的垃圾总量为　　　　　 万吨。已知2001年产生的垃圾量为5万吨，求从2001年初至2003年末产生的垃圾量的年平均增长率是多少？

（参考数据：；结果保留两个有效数字）

（2）若2004年初，该城市新建的垃圾处理厂投入运行，打算到2008年底前把所堆积的新、旧垃圾全部处理完，则该厂平均每年至少需处理垃圾多少万吨？

23、（本题满分8分）

我们已经知道，如果线段MN被点P分成线段MP和PN，且，那么称线段MN被点P黄金分割，点P叫做线段MN的黄金分割点，MP与MN的比叫做黄金比。通过计算可知黄金比为。

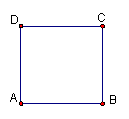
若一个矩形的短边与长边之比等于黄金比，则称这个矩形为黄金矩形。

已知图中正方形ABCD的边长为1，请你以AD为短边，用尺规作一个黄金矩形，要求保留作图痕迹并简要写出做法，不要求证明。

24、（本题满分9分）

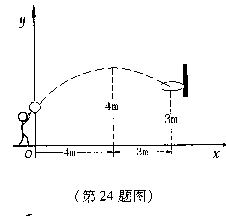
某校初三年级的一场篮球比赛中，如图队员甲正在投篮，已知球出手时离地面高m，与篮圈中心的水平距离为7m，当球出手后水平距离为4m时到达最大高度4m，设篮球运行的轨迹为抛物线，篮圈距地面3m。

1）  建立如图的平面直角坐标系，问此球能否准确投中？

2）  此时，若对方队员乙在甲前面1m处跳起盖帽拦截，已知乙的最大摸高为3.1m，那么他能否获得成功？

25、（本题满分11分）

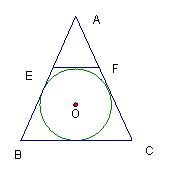如图△ABC中，AB=AC, EF//BC, 且⊙O内切于四边形BCFE。

1）当时,sinB=　　　　  .

2) 当时，sinB等于多少？请说明理由。

26、（本题满分13分）

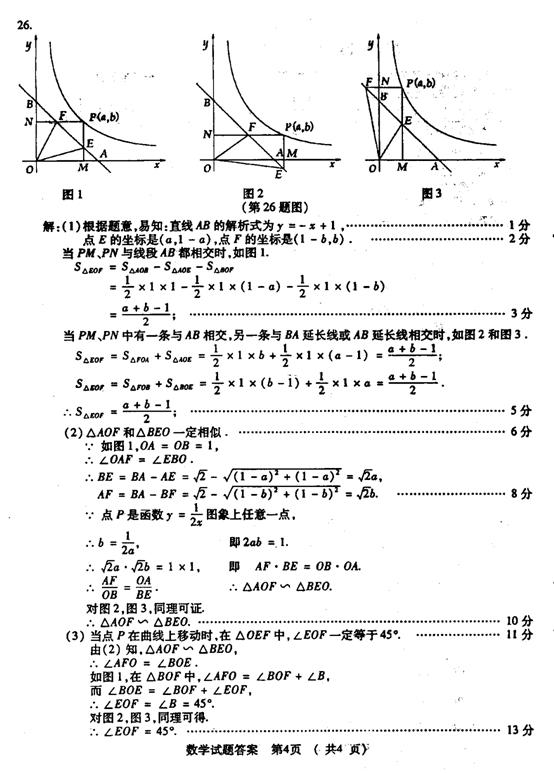
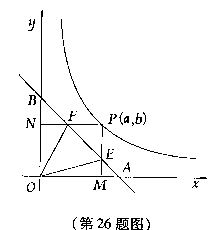如图，已知直角坐标系内有一条直线和一条曲线，这条直线和x轴、y轴分别交于点A和点B，且OA＝OB＝1，这条曲线是函数y＝的图像在第一限内的一个分支，点P是这条曲线的任意一点，它的坐标是（a，b），由点P向x轴、y轴所作的垂线PM、PN（点M、N为垂足）分别与直线AB相交于点E和F。

1）  求△OEF的面积（a，b的代数式表示）；

2）  △AOF与△BOE是否一定相似，如果一定相似，请证明；如果不一定相似，请说明理由；

3）  当点P在曲线上移动时，△OEF随之变动，指出在△OEF的三个内角中，是否有大小始终保持不变的角？若有，请求出其大小；若没有，请说明理由。