中考数学模拟试题(15)

一．大胆尝试，选择最佳:

1．你认为下列各式正确的是（　　 ）毛

A. a²=(-a ) ²　　 B.a³=(-a) ³　　　C.-a²=　　　　D. a³=

2 从甲站到乙站有两种走法。从乙站到丙站有三种走法。从乙站到丙站有______种走法。

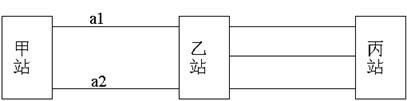
A. 4　 　 B. 5　　 　　C. 6　　　　 D.7

3．通常C表示摄氏温度，f表示华氏温度，C与f之间的关系式为： ,当华氏温度为68时，摄氏温度为（　 ）

A. -20　　　B. 20　　　 C. -19　　　 D. 1 9

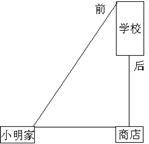
4．从小明家到学校有两条路。一条沿北偏东45度方向可直达学校前门，另一条从小明家一直往东，到商店处向正北走200米，到学校后门。若两条路的路程相等，学校南北走向。学校的后门在小明家北偏东67.5度处。学校从前门到后门的距离是（　　 ）米。

　  A.200米;B.200米;C.200米;D.200米

5． 小红的妈妈问小兰今年多大了，小兰说："小红是我现在的年龄时，我十岁；我是小红现在的年龄时，小红25岁。"小红的妈妈立刻说出了小兰的岁数，小兰与小红差（　）岁。

A.10　　B.8　　　C.5　　　D.2

 6．梯子跟地面的夹角为A，关于∠A的三角函数值与梯子的倾斜程度之间，叙述正确的是（　　 ）

A. sinA的值越小，梯子越陡。

B. cosA的值越小，梯子越陡。

C. tanA的值越小，梯子越陡。

D. 陡缓程度与∠A的函数值无关。

7.某兴趣小组做实验，将一个装满水的酒瓶倒 置，并设法使瓶里的水从瓶口匀速流出，那么该倒置酒瓶内水面高度h随水流出时。水面高度h与水流时间t之间关系的函数图象为（　　）

8. 一矩形纸片绕其一边旋转180度后，所得的几何体的主视图和俯视图分别为（　　　）

A、矩形，矩形　　B、圆，半圆　　　　  C、圆，矩形 　 D、矩形，半圆

9.二次函数y=-2(x-1)²+3的图象如何移动就得到y=-2x²的图象（　　　）

A. 向左移动1个单位，向上移动3个单位。

B. 向右移动1个单位，向上移动3个单位。

C. 向左移动1个单位，向下移动3个单位。

D. 向右移动1个单位，向下移动3个单位。

10. 2001年7月13日，北京市获得了第29届运动会的主办权，这一天是星期五，那么第29届奥运会在北京市举办的那一年的7月13日是星期(　　 )

A.1　　　　B. 3　　　  C. 5　　　　D. 日

二、相信自己，成功在握:

1. 地球上的陆地面积约为千米²。用科学记数法保留两位有效数字为____________千米²。

2. 春天来了天气一天比一天暖和，在同一地点某一物体，今天上午11点的影子比昨天上午11点的影子__________。（长，短）

3.一个矩形的面积为20cm² ，相邻两条边长分别为x cm和y cm，那么变量y与变量x的函数关系式为_________。

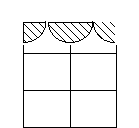
4.一个窗户被装饰布档住一部分，其中窗户的长与宽之间比为3:2装饰布由一个半圆和两个四分之一圆组成，圆的直径都是,这个窗口未被遮挡部分的面积为__________。

5.一个圆弧形拱桥的跨度为6cm，桥的拱高为1cm，那么拱桥的半径是________。

6.国旗是一个国家的象征，在中国、美国、瑞士三国的国旗中既是中心对称，又是轴对称的是______________国的国旗。

7、观察下列各式：（x-1）(x+1)=x²-1

(x-1)(x²+x+1)=x³-1

(x-1)(x³+x²+x+1)=x⁴-1

根据前面各式的规律可得到(x-1)(xⁿ+x^n-1+x^n-2+…+x+1)=____________。

8、掷一枚均匀的骰子，每次实验掷两次，两次骰子的点数之和为6的概率为___________。

9、如不等式mx+n<0的解集是x>4，点（1，n）在双曲线y=上，那么函数y=(n-1)x+m的图像不通过第_________象限。

10、用一只平地锅煎饼，每次只能放2只饼，煎一只需要2分钟，（规定正反各需1分钟），如果煎n(n>1)只饼，至少需__________分钟。

三、解答题：

1、化繁为简，轻松计算：已知:, 求 (2a+1)²-(2a+1)(2a-1)的值。

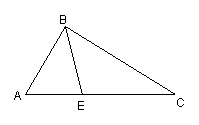
2、已知：△ABC中，∠B=90°，BE平分∠ABC , AB=6cm , AC=10cm 。

(1)在BE的延长线上求作一点D，使DA=DC;

(2)四边形ABCD是否有外接圆，并说明理由。若有求外接圆的面积；若没有说明理由。

四、　帮忙算一算:

中兴农场要建立一个长方形的养鸡场，鸡场的一边靠墙，墙长25米另三边用木栏围成。木栏长40米，

(1)鸡场的面积能达到180cm²吗？能达到200cm²吗？

(2）鸡场的面积能达到250cm²吗？

五　勇于探索，努力闯关:

在“仓库世家”游戏中，游戏规则为“只要将所有木箱归位，便可过关，可以左右上下转身，推动木箱只可前进，无法后拉，按 8，2，4，6 可上下左右移动。

数字	表示
8	上移一格
2	下移一格
4	左移一格
6	右移一格

（△代表木箱，☆代表木箱应到的目的地，□代表空地，　 代表墙壁，移动一次只动一个格）其中第一关是如图一设计。移动方案为：→4→8→2→6→6→6→8→8→8。

下图为第三关，请你设计出移动方案:

方案为：→

六. 民以食为天:

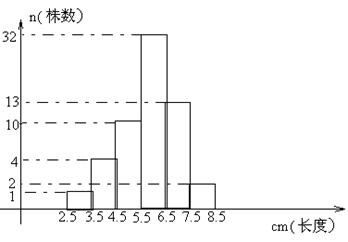
为研究成熟小麦的麦穗长度，腾飞中学组织学生到校实验田调查，要求按自己收集数据进行整理，并得出结论。请帮小颖把报告单填好，并回答下列问题：

题目	了解当地成熟小麦的穗长
样本来源	腾飞中学试验田	样本容量	60
获取方法	从该校实验田任取60株成熟小麦测出其穗长，并记录
样本数据的整理
结论

问题:

1.样本数据的整理运用了____________统计图，这种统计图的特点是___________________________________________________________________________。

2.此题还可用扇形统计图表示，这种统计图的特点是：___________________________________________________________________________。

3.我们还学过折线统计图，这种统计图的特点是：___________________________________________________________________________。

七 修路护路，环境保护:

为收回建路成本，更好的保养公路，设立了公路收费站，某兴趣小组对一个收费站通过车辆情况做了调查，数据如下：

时间	第1分钟	第2分钟	第3分钟	第4分钟	第5分钟	第7分钟	第8分钟	第9分钟	第10分钟
通过车辆数	24	23	25	22	26	23	24	25	24

⑴利用上述数据求平均每分钟通过多少车辆，并估计一天通过的车辆数。

⑵收费站规定，一辆机动车通过一次原则上收费20元，以保护环境为根本，达到环保指标的减少1元收费，不达标的多收2元，若某天的总收入为y元，通过的达标车辆是不达标车辆的x倍，求x与y之间的函数关系式。

此段公路修建花费70万元，收费站每天还要拿出100元用于修建费用，问：x为多少时，收费站能在三年内收回成本。

参考答案

一、选择题:1.　A　2.C　 3.B　 4.B　 5.C　 6.B　 7.B　8.D　 9.C　 10.D

二、填空题:1. 1.5×10⁸ 　 2. 短  　3. y=　　4.,

　 5. 5cm　 6. 瑞士　 7. xⁿ⁺¹ -1　 8.  　9. 一　 10.n

三、

1、（2a+1）²-(2a+1)(2a-1)=4a²+4a+1-4a²+1=4a+2,

当a=时,

2 、(1)作AC的垂直平分线MN，与AC交于O点，与BE延长线交点为求作点D。　　

(2)有外接圆　

连结AD、CD，过D点作DE、DF分别垂直于AB、CB。

由△EDA≌△FDC得OA=OB=OC=OD, =25.

四、设鸡场的一边为xcm,另外两边均为cm,　

x×=180, x₁=20+2, x₂=20-2,能达180m².

当x×=200,x₁= x₂=20,能达到200m² ;

当x×=250,方程无解,不能达到.　　　

五、多种方式，合理即可.

六、结论（与统计知识有关即可，至少写3个）　　

(1)条形，（能清楚地表示出每个项目的具体数目　

(2)能清楚地反映事物的变化情况

(3)能清楚地表示出各部分在总体中所占的百分比

七、(1）（24+23+……+24）÷9=24　

一天：24×24×60=34560

(2)　

(3) 700000+100×3×365=

x≈1.8（倍.毛