初三代数总复习

一、　　　　　  填空题：

1.　　　  一种细菌的半径约为0.000045米，用科学记数法表示为　　　　　米．

2.　　　  的立方根是　　　，的平方根是　　　；

3.　　　  如果a+2+=0，那么a、b的大小关系为a　　　　b(填“＞”“=”或“<”)；

4.　　　  计算：=　　　　　　 。

5.　　  计算：+―=　　　　　  。

6.　　　在实数范围内分解因式：ab²－2a＝___　　　　______.

7.　　　  计算：＋＝　　　　　　  。

8.　　　 不等式组的解集是____________。

9.　　　  方程的解是__ ___ x=5_____________.

10.　  观察下列等式，×2 = +2，×3 = +3，×4 = +4，×5 = +5

设表示正整数，用关于的等式表示这个规律为_______　　 ____；

11.　在函数中，自变量x的取值范围是____________。

12.　如果反比例函数的图象经过点（1，-2），那么这个反比例函数的解析式为_________________。

13.　  函数与轴的交点是　　　　　  ，与轴的交点是　　　　　　 ，与两坐标轴围成的三角形面积是　　　　  ；

14.　  某地的电话月租费24元，通话费每分钟0.15元，则每月话费（元）与通话时间（分钟）之间的关系式是　　　　　　　　　　 ，某居民某月的电话费是38.7元，则通话时间是　　　　 分钟，若通话时间62分钟，则电话费为　　　　　  元；

15.　  函数的图像，在每一个象限内，随的增大而　　　；

16.　  把函数的图象向右平移3个单位，再向下平移2个单位，得到的二次函数解析式是　　　　　　　  ；

17.　　把二次函数化成的形式是　　　　　　　 ，顶点坐标是　　　　　　　　 ，对称轴是　　　　　　　　　 ；

18.　　1，2，3，的平均数是3，则3，6，的平均数是　　　　  ；

19.　  2004年5月份，某市市区一周空气质量报告中某项污染指数的数据是：31　35  31　34　30  32　31 这组数据的中位数是　　　　　　　　　　 ；

20.　  为了调查某校初中三年级240名学生的身高情况，从中抽测了40名学生的身高，在这个问题中总体是　　　　，个体是　　　　  ，样本是　　　　　　 ；

21.　  点P(，)关于轴的对称点的坐标是 　　　　　 ，关于轴的对称点的坐标是　　　　　　 ，关于原点的对称点的坐标是　　　　　　 ；

22.　  若点 在第一象限，则的取值范围是 　　　　　　　　　 ；

23.　  已知，化简的结果是　　　　　　　　  ；

24.　  方程的根是，则可分解为 　　　　　　　　　 ；

25.　  方程的解是；

26.　  方程  的一根是，则它的另一根是 　　　　 ， ；

27.　  已知时，分式无意义，时此分式值为0，则；

28.　  若方程组的解是，则a＝_________，b＝_______；

29.  10张卡片分别写有0至9十个数字,将它们放入纸箱后,任意摸出一张,则P(摸到数字2)=　　 0.1 　,P(摸到奇数)=  0.5  　　 ；

30.　  甲、乙两人进行射击比赛，在相同条件下各射击 10 次他们的平均成绩均为 7 环10 次射击成绩的方差分别是：，．成绩较为稳定的是____乙______．（填“甲”或“乙” ）

二、选择题：

31、在实数π，2，，，tan45°中，有理数的个数是　　 （　　）

A、 2个　　　B、3个　 　 C、  4个　 　D、5个

32、下列二次根式中与是同类二次根式的是　（　 ）
　　 A、 　　 B、 　　　C、　　  D、

33、在下列函数中，正比例函数是 （　　）

 A　　 　　 B 　　　C　 　　 D　

34、李老师骑自行车上班，最初以某一速度匀速行进，中途由于自行车发生故障，停下修车耽误了几分钟，为了按时到校，李老师加快了速度，仍保持匀速前进，结果准时到校，在课堂上，李老师请学生画出：自行车行进路程Ｓ（千米）与行进时间t（小时）的函数图象的示意图，同学们画出的示意图如下，你认为正确的是　　　　　　　　　　　　　　  （　　）

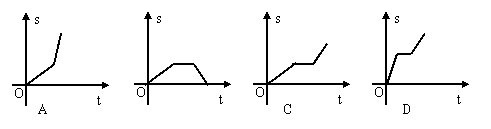　　　　　　　　　  B

35、正比例函数和反比例函数在同一坐标系内的图象为　　　　　　 

（　　）

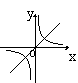
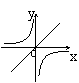
A　　　　　　　　　　　　 B　　　　　　　　　　　　　C　　　　　　　　　　 　　　 D

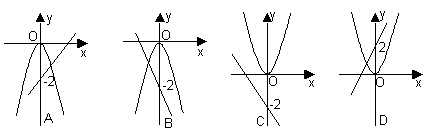
36、二次函数，则它的图象必经过点　　　　　　　 （　　）

A　（，）  B （，） 　 C　（，） 　D （，）

37、不等式组的整数解的个数是　 （　 ）　　　　　　　　　　　　　　　 

A　 1　　　 B　　2　　　　C　　3　　　D　　4

38、在同一坐标系中，作出函数和的图象，只可能是　　 （　　）

39、若关于的方程有两个相等的实根，则a的值是　　　　　 （　　）

A　 －4　　　　B　 4　　　　C　　4或－4　　 D　 2

40、某中学为了了解初中三年级数学的学习情况，在全校学生中抽取了50名学生进行测试(成绩均为整数，满分为100分)，将50名学生的数学成绩进行整理，分成5组画出的频率分布直方图如图所示，已知从左至右4个小组的频率分别是0.06，0.08，0.20，0.28，那么这次测试学生成绩为优秀的有(分数大于或等于80分为优秀)。　（　　）　　　　　　　　　　　　　　　　

A　 30人　　B 　31人　　C　  33人　　D　 34人

41、某学校用420元钱到商场去购买“84”消毒液，经过还价，每瓶便宜0.5元，结果比用原价多买了20瓶，求原价每瓶多少元？若设原价每瓶元，则可列出方程为　　　　 （　　）

A　 　　　　　B　

C　 　　　　　D　

42、在边长为a的正方形中挖去一个边长为b的小正方形（a>b）（如图1），把余下的部分拼成一个矩形（如图2），根据两个图形中阴影部分的面积相等，可以验证（  C 　）

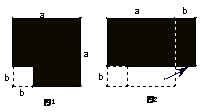（A）

（B）

（C）

（D）

三、解答题：

43、计算： ；　　　　

 44、计算：

　　　　　 

45、解不等式组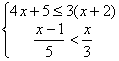

46、抛物线的对称轴是，且过（4，－4）、（－1，2），求此抛物线的解析式；

47、为了保护学生的视力，课桌椅的高度是按一定的关系配套设计的。研究表明：假设课桌的高度为cm，椅子的高度（不含靠背）为cm，则应是的一次函数，右边的表中给出两套符合条件的桌椅的高度：

	第一套	第二套
椅子高度（cm）	40.0	37.0
桌子高度（cm）	75.0	70.2

（1）请确定与的函数关系式；

（2）现有一把高42.0cm的椅子和一张高78.2cm的课桌，它们是否配套？请通过计算说明理由。

48、有一个抛物线形拱桥，其最大高度为16m，跨度为40m，现把它的示意图放在平面直角坐标系中如 图（4），求抛物线的解析式

 

 

 

49、某工厂第一季度生产甲、乙两种机器共480台．改进生产技术后，计划第二季度生产这两种机器共554 台，其中甲种机器产量要比第一季度增产10 % ，乙种机器产量要比第一季度增产20 % ．该厂第一季度生产甲、乙两种机器各多少台？

50、为节约用电，某学校于本学期初制定了详细的用电计划。如果实际每天比计划多用2度电，那么本学期的用电量将会超过2530度；如果实际每天比计划节约2度电，那么本学期用电量将会不超过2200度电。若本学期的在校时间按110天计算，那么学校每天用电量应控制在什么范围内？

51、某公司销售部有营销人员15人，销售部为了制定某种商品的月销售定额，统计了这15人某月的销售量如下：

每人销售件数	1800	510	250	210	150	120
人数	1	1	3	5	5	2

（1）求这15位营销人员该月销售量的平均数、中位数和众数；

（2）假设销售部负责人把每位营销员的月销售额定为320件，你认为是否合理，为什么？如果不合理，请你制定一个较合理的销售定额，并说明理由；

52、小刚为书房买灯，现有两种灯可供选择，其中一种是9瓦（0.009千瓦）的节能灯，售价49元/盏；另一种是40瓦（0.04千瓦）的白炽灯，售价18元/盏。假设两种灯的照明亮度一样，使用寿命都可以达到2800小时，并已知小刚家所在地的电价是每千瓦时0.5元。

（1）设照明时间是小时，设一盏节能灯的费用和一盏白炽灯的费用，求出与之间的函数关系式（注：费用=灯的售价+电费）

（2）小刚想在这两种灯中选一盏。

①当照明时间是多少时，使用两种灯的费用一样多？

②照明时间是在什么范围内，选用白炽灯的费用最低？

③照明时间是在什么范围内，选用节能灯的费用最低？

（3）小刚想在这两种灯中选购两盏。

假定照明时间是3000小时，使用寿命就是2800小时。请你帮他设计一种费用最低的选灯方案，并说明理由。

答案：

一、填空题

1）、4.5×10^-5　 2）、-2，　　3）、<　　 4）、2　　 5）、0　

 6）、a(b-)(b+)　 7）、1　  8）、　　 9）、x=5　

 10）、

11）、　 12）、　　13）、　 14）、y=0.15x+24，（、98，3.33　

15）、增大　 16）、y=2(x-3)²-2　　17）、y=(x-2)²+4　18）、5 19）、31

20）、某校初中三年级240名学生的身高，一名学生的身高，某校初中三年级40名学生的身高

21）、（-1,-2）（1,2）（1,-2）　  22）、　　23）、1　  24）、

25）、　　26）、-1，2　　27）、6　　 28）、-5，3　　29）、，　　30、乙

二、选择题

31、B　 32、D　 33、A 34、C 35、B 36、C 37、C 38、B 39、B

40、C 41、B 42、C　

三、解答题

43）、4　　　44）、　 45）、　　 　46）、

47）、(1)y=1.6x+11  (2)当高为4.20cm时，y=42×1.6+11=78.2 它们是配套的

48）、依题意得：A(20，16)　 B（0，40）  设　  k=0.06　　　　　

49）、解：设第一季度生产甲机器x台，乙机器y台

　　 　　 解得：

答：甲机器220台，乙机器260台。

50、解：设每天用电量为x度。

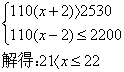
51、（1）平均数：340　 中位数：210　　 众数：210，150　　

（2）不合理；因为销售额等达到320件的人只有2人，还有13人不能达到。可以把销售额定为210件。因为中位数为210，众数为210，说明有大多数的人可以达到。

52、1）　

2）①由，解得②由，解得③由，解得

3）如果选用两盏节能灯，则费用是111.5元；如果选用两盏白炽灯，则费用是96元；如果选用一盏节能灯和一盏白炽灯，由（2）可知，当照明时间大于2000小时时，用节能灯比白炽灯费用低，所以节能灯用完2800小时时，费用最低，费用是83.6元。

因此，因选一盏灯，且节能灯使用2800小时，白炽灯使用200小时费用最低。