中考数学试题汇编(一次方程(组))
一、选择题
1、(2007陕西课改)中国人民银行宣布,从2007年6月5日起,上调人民币存款利率,一年定期存款利率上调到3.06%.某人于2007年6月5日存入定期为1年的人民币5000元(到期后银行将扣除20%的利息锐).设到期后银行应向储户支付现金![]() 元,则所列方程正确的是( )C
元,则所列方程正确的是( )C
A.![]()
B.![]()
C.![]()
D.![]()
2、(2007浙江丽水)方程组![]() ,由②
,由②![]() ①,得正确的方程是( )B
①,得正确的方程是( )B
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
3、(2007江苏苏州)方程组![]() 的解是 ( )D
的解是 ( )D
A.![]() B.
B.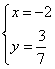 C.
C.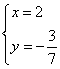 D.
D.![]()
4、(2007湖南株州)二元一次方程组![]() 的解是:( ) A
的解是:( ) A
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
5、(2007山东淄博)若方程组 ![]() 的解是
的解是 ![]() 则方程组
则方程组
![]() 的解是( )A
的解是( )A
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
6、(2007广州)以![]() 为解的二元一次方程组是( )C
为解的二元一次方程组是( )C
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7、(2007四川东山)某蔬菜公司收购到某种蔬菜140吨,准备加工上市销售.该公司的加工能力是:每天可以精加工6吨或粗加工16吨.现计划用15天完成加工任务,该公司应按排几天精加工,几天粗加工?设安排![]() 天精加工,
天精加工,![]() 天粗加工.为解决这个问题,所列方程组正确的是( )D
天粗加工.为解决这个问题,所列方程组正确的是( )D
A.![]() B.
B.![]()
C.![]() D.
D.![]()
8、(2007湖北宜宾)某班共有学生49人.一天,该班某男生因事请假,当天的男生人数恰为女生人数的一半.若设该班男生人数为x,女生人数为y,则下列方程组中,能正确计算出x、y的是( )D
A. B. C. D.
9、(2007浙江舟山)三个同学对问题“若方程组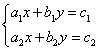 的解是
的解是![]() ,求方程组
,求方程组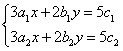 的解.”提出各自的想法.甲说:“这个题目好象条件不够,不能求解”;乙说:“它们的系数有一定的规律,可以试试”;丙说:“能不能把第二个方程组的两个方程的两边都除以5,通过换元替代的方法来解决”.参考他们的讨论,你认为这个题目的解应该是 .
的解.”提出各自的想法.甲说:“这个题目好象条件不够,不能求解”;乙说:“它们的系数有一定的规律,可以试试”;丙说:“能不能把第二个方程组的两个方程的两边都除以5,通过换元替代的方法来解决”.参考他们的讨论,你认为这个题目的解应该是 .
![]()
二、填空题
1、(2007湖南湘潭)某市在端年节准备举行划龙舟大赛,预计15个队共330人参加.已知每个队一条船,每条船上人数相等,且每条船上有1人击鼓,1人掌舵,其余的人同时划桨.设每条船上划桨的有![]() 人,那么可列出一元一次方程为
.
人,那么可列出一元一次方程为
.
答:15(![]() +2)=330
+2)=330
2、(2007湖南怀化)方程组![]() 的解是 .
的解是 .![]()
3、(2007浙江杭州)三个同学对问题“若方程组![]() 的解是
的解是![]() ,求方程组
,求方程组![]() 的解。”提出各自的想法。甲说:“这个题目好象条件不够,不能求解”;乙说:“它们的系数有一定的规律,可以试试”;丙说:“能不能把第二个方程组的两个方程的两边都除以5,通过换元替换的方法来解决”。参考他们的讨论,你认为这个题目的解应该是
。
的解。”提出各自的想法。甲说:“这个题目好象条件不够,不能求解”;乙说:“它们的系数有一定的规律,可以试试”;丙说:“能不能把第二个方程组的两个方程的两边都除以5,通过换元替换的方法来解决”。参考他们的讨论,你认为这个题目的解应该是
。
![]()
4、(2007山东青岛)某市在旧城改造过程中,需要整修一段全长2400m的道路.为了尽量减少施工对城市交通所造成的影响,实际工作效率比原计划提高了20%,结果提前8小时完成任务.求原计划每小时修路的长度.若设原计划每小时修路x m,则根据题意可得方程 .
![]()
5、(2007山东济宁)南水北调东线工程已经开工,某施工单位准备对运河一段长2240m的河堤进行加固,由于采用新的加固模式,现计划每天加固的长度比原计划增加了20m,因而完成河堤加固工程所需天数将比原计划缩短2天,若设现在计划每天加固河堤xm,则得方程为 。
![]() -
-![]() =2
=2
6、(2007湖南益阳)某市处理污水,需要铺设一条长为1000M的管道,为了尽量减少施工对交通所造成的影响,实际施工时,每天比原计划多铺设10米,结果提前5天完成任务。设原计划每天铺设管道xm,则可得方程 。
![]() -
-![]() =5
=5
7、(2007贵阳)方程![]() 的解为
的解为![]() .4
.4
8、(2007湖南岳阳)分式方程-1=0的解是____________ (答案:x=-1)
三、解答题
1、(2007山东青岛)解方程组:![]()
|
①×3,得 6x+3y=15. ③
②+③,得 7x=21,
x=3. …………………………3′
把x=3代入①,得2×3+y=5,y=-1.
∴原方程组的解是![]()
2、(2007浙江金华)解方程组:![]()
解:![]() 得:
得:![]() ,
,![]() ,
,
把![]() 代入①得:
代入①得:![]() ,
,![]()
3、(2007江苏南京)解方程组![]()
解:①+②,得![]() .解得
.解得![]() .
.
把![]() 代入②,得
代入②,得![]() .
.
![]() 原方程组的解是
原方程组的解是![]()
4、(2007甘肃陇南)解方程x(x![]() 1)=2.
1)=2.
有学生给出如下解法:
∵ x(x![]() 1)=2=1×2=(
1)=2=1×2=(![]() 1)×(
1)×(![]() 2),
2),
∴ ![]() 或
或![]() 或
或![]() 或
或![]()
解上面第一、四方程组,无解;解第二、三方程组,得 x=2或x=![]() 1.
1.
∴ x=2或x=-![]() 1.
1.
请问:这个解法对吗?试说明你的理由.
解:答案一:
对于这个特定的已知方程,解法是对的.
理由是:一元二次方程有根的话,只能有两个根,此学生已经将两个根都求出来了,所以对.
答案二:
解法不严密,方法不具有一般性.
理由是:为何不可以2=3×![]() 等,得到其它的方程组?此学生的方法只是巧合了,求对了方程的根.
等,得到其它的方程组?此学生的方法只是巧合了,求对了方程的根.
5、(2007江苏连云港)解方程:![]() .
.
解:方程两边同乘![]() ,得
,得![]() .
.
解这个方程,得![]() .
.
检验:当![]() 时,
时,![]() ,所以
,所以![]() 是增根,原方程无解
是增根,原方程无解
6、(2007湖北孝感)解分式方程:![]()
解:方程两边同乘以2(3x-1),去分母,
得 -2-3(3x-1)=4 ………………………………………2分
解这个整式方程,得
![]() ………………………………………4分
………………………………………4分
检验:把![]() 代入最简公分母2(3x-1)=2(-1-1)=-4≠0.
代入最简公分母2(3x-1)=2(-1-1)=-4≠0.
∴原方程的解是![]()
7.(山东德州)解方程:![]() .
.
解:两边同乘以![]() ,
,
得![]() ;········································································· 3分
;········································································· 3分
整理,得![]() ;
;
解得 ![]() .········································································································ 5分
.········································································································ 5分
经检验,![]() 是原方程的根.
是原方程的根.
8、(2007浙江宁波)解方程![]() .
.
解:方程两边同乘(x-2)(x+2),得
x(x+2)-(x2-4)=1,……………………2分
化简,得2x=-3……………………4分
x=-3/2,……………………5分
经检验,x=-3/2是原方程的根.
9、(2007安徽芜湖)芜湖供电公司分时电价执行时段分为平、谷两个时段,平段为8:00~22:00,14小时,谷段为22:00~次日8:00,10小时.平段用电价格在原销售电价基础上每千瓦时上浮0.03元,谷段电价在原销售电价基础上每千瓦时下浮0.25元,小明家5月份实用平段电量40千瓦时, 谷段电量60千瓦时,按分时电价付费42.73元.
(1)问小明该月支付的平段、谷段电价每千瓦时各为多少元?
(2)如不使用分时电价结算, 5月份小明家将多支付电费多少元?
解:(1)设原销售电价为每千瓦时x元,根据题意得: ……………………………1分
![]() ………………………………3分
………………………………3分
![]()
![]()
![]() .
………………………………4分
.
………………………………4分
∴当![]() 时,
时,![]() ;
;![]() .
.
答:小明家该月支付平段电价为每千瓦时0.5953元、谷段电价每千瓦时0.3153元.……6分
(2) ![]() (元)
(元)
答:如不使用分时电价结算,小明家5月份将多支付13.8元.
10、(2007上海市)2001年以来,我国曾五次实施药品降价,累计降价的总金额为269亿元,五次药品降价的年份与相应降价金额如表二所示,表中缺失了2003年、2007年相关数据.已知2007年药品降价金额是2003年药品降价金额的6倍,结合表中信息,求2003年和2007年的药品降价金额.
| 年份 | 2001 | 2003 | 2004 | 2005 | 2007 |
| 降价金额(亿元) | 54 | 35 | 40 |
表二
解:[解法一]设2003年和2007年的药品降价金额分别为![]() 亿元、
亿元、![]() 亿元.·················· 1分
亿元.·················· 1分
根据题意,得![]()
解方程组,得![]()
答:2003年和2007年的药品降价金额分别为20亿元和120亿元.································ 1分
[解法二]设2003年的药品降价金额为![]() 亿元,······························································ 1分
亿元,······························································ 1分
则2007年的药品降价金额为![]() 亿元.·········································································· 2分
亿元.·········································································· 2分
根据题意,得![]() .································································· 2分
.································································· 2分
解方程,得![]() ,
,![]() .··············································································· 4分
.··············································································· 4分
答:2003年和2007年的药品降价金额分别为20亿元和120亿元.
11、(2007浙江宁波)2007年5月19日起,中国人民银行上调存款利率.
人民币存款利率调整表
| 项 目 | 调整前年利率% | 调整后年利率% |
| 活期存款 | 0.72 | 0.72 |
| 二年期定期存款 | 2.79 | 3.06 |
储户的实得利息收益是扣除利息税后的所得利息,利息税率为20%.
(1)小明于2007年5月19日把3500元的压岁钱按一年期定期存入银行,到期时他实得利息收益是多少元?
(2)小明在这次利率调整前有一笔一年期定期存款,到期时按调整前的年利率2.79%计息,本金与实得利息收益的和为2555.8元,问他这笔存款的本金是多少元?
 (3)小明爸爸有一张在2007年5月19日前存人的10000元的一年期定期存款单,为获取更大的利息收益,想把这笔存款转存为利率调整后的一年期定期存款.问他是否应该转存?请说明理由.
(3)小明爸爸有一张在2007年5月19日前存人的10000元的一年期定期存款单,为获取更大的利息收益,想把这笔存款转存为利率调整后的一年期定期存款.问他是否应该转存?请说明理由.
约定:
①存款天数按整数天计算,一年按360天计算利息.
②比较利息大小是指从首次存入日开始的一年时间内.获得的利息比较.如果不转存,利息按调整前的一年期定期利率计算;如果转存,转存前已存天数的利息按活期利率计算,转存后,余下天数的利息按调整后的一年期定期利率计算(转存前后本金不变).
解:(1)3500×3.06%×80%=85.68(元),
∴到期时他实得利息收益是85.68元.………………………………2分
(2)设他这笔存款的本金是x元,
则x(1+2.79%×80%)=2555.8,……………………………………4分
解得x=2500,
∴这笔存款的本金是2500元.……………………………………6分
(3)设小明爸爸的这笔存款转存前已存了x天,由题意得
l0000×![]() ×0.72%+10000×
×0.72%+10000×![]() ×3.06%>10000×2.79%,………………8分
×3.06%>10000×2.79%,………………8分
解得x<41![]() ,……………………9分
,……………………9分
当他这笔存款转存前已存天数不超过41天时;他应该转存;否则不需转存.……………………10分
12、(2007恩施自治州)团体购买公园门票票价如下:
| 购票人数 | 1~50 | 51~100 | 100人以上 |
| 每人门票(元) | 13元 | 11元 | 9元 |
今有甲、乙两个旅行团,已知甲团人数少于50人,乙团人数不超过100人.
若分别购票,两团共计应付门票费1392元,若合在一起作为一个团体购票,总计
应付门票费1080元.
(1)请你判断乙团的人数是否也少于50人.
(2)求甲、乙两旅行团各有多少人?
解:(1)∵100×13=1300<1392
∴乙团的人数不少于50人,不超过100人 (2分)
(2)设甲、乙两旅行团分别有x人、y人, (3分)
则![]() (6分)
(6分)
解得:![]() (7分)
(7分)
所以甲、乙两旅行团分别有36人、84人