初三数学第一学期夜课甲班练习（7）　　　　姓名：____________

1．李明设计了下面四种正多边形的瓷砖图案，用同一种瓷砖可以平面密铺的是（　　）

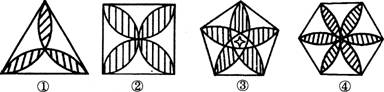
Ａ．①②④　　　　　　　　　Ｂ．②③④　　　　　　　　　Ｃ．①③④　　　　　　　　　Ｄ．①②③

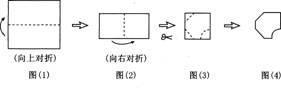2．将一个正方形纸片依次按图（1），图（2）方式对折，然后沿图（3）中的虚线裁剪，最后将图（4）的纸再展开铺平，所看到的图案是（　　）

3．已知二次函数，其中满足a+b+c=0和9a-3b+c=0，则该二次函数图象的对称轴是（　　）

Ａ．　　　　　　　　　Ｂ．　　　　　 Ｃ．　　　Ｄ．

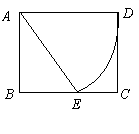
4．如图，已知矩形纸片ABCD，AD=2,，，以A为圆心， AD长为半径画弧交BC于点E，将扇形AED剪下围成一个圆锥，则该圆锥的底面半径为（　　）

Ａ．1　　 　　　　　　　Ｂ．　　　　　　　　 Ｃ．　　　　　　　　　Ｄ．

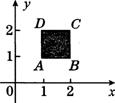5．如图，有一种动画程序，屏幕上正方形是黑色区域（含正方形边界），其中，用信号枪沿直线发射信号，当信号遇到黑色区域时，区域便由黑变白，则能够使黑色区域变白的的取值范围为　　　　　．

6．如果反比例函数的图象位于第二、四象限内，那么满足条件的正整数的值是　　　　．

7．已知等腰三角形ABC中，AB=AC,D为BC边上一点，连接AD，若△ACD和△ABD都是等腰三角形，则∠C的度数是　　　　．

8．观察下列等式：，，，，，，，……．通过观察，用你所发现的规律确定的个位数字是　　　　．

9．如图，已知在⊙O中，直径MN=10，正方形ABCD的四个顶点分别在半径OM，OP以及⊙O上，并且∠POM=45°，则AB的长为　　　　．

10．已知一元二次方程有两个不相等的实数根，则k的最大整数值为　　　　　．

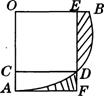11．如图，扇形OAB的圆心角为，四边形OCDE是边长为1的正方形，点C,E,D分别在OA,OB，︵AB上，过点作交的延长线于点，那么图中阴影部分的面积为　　　　　．

12．如图，在方格纸（每个小方格都是边长为1个单位长度的正方形）中，我们称每个小正方形的顶点为格点，以格点为顶点的图形称为格点图形．如图中的△ABC称为格点△ABC．

（1）如果A，D两点的坐标分别是(1，1)和(0，1)，请你在方格纸中建立平面直角坐标系，并直接写出点B，点C的坐标；

（2）请根据你所学过的平移、旋转或轴对称等知识，说明图中“格点四边形图案”是如何通过“格点△ABC图案”变换得到的．

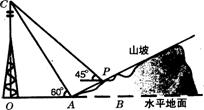
13．如图，某人在山坡坡脚处测得电视塔尖点的仰角为，沿山坡向上走到处再测得点C的仰角为，已知OA=100米，山坡坡度且O,A,B在同一条直线上．求电视塔OC的高度以及此人所在位置点的铅直高度．（测倾器高度忽略不计，结果保留根号形式）

14．已知BC为⊙O直径，D是直径BC上一动点（不与点B,O,C重合），过点D作直线AH⊥BC交⊙O于A，H两点，F是⊙O上一点（不与点B，C重合），且︵AB=︵AF，直线BF交直线AH于点E．

（1）如图（a），当点D在线段BO上时，试判断AE与BE的大小关系，并证明你的结论；

（2）当点D在线段OC上，且OD>DC时，其它条件不变．

①请你在图（b）中画出符合要求的图形，并参照图（a）标记字母；

②判断（1）中的结论是否还成立，请说明理由．

15．如图，四边形OABC是一张放在平面直角坐标系中的正方形纸片．点O与坐标原点重合，点A在x轴上，点C在y轴上，OC=4，点为BC的中点，点的坐标为，过点且平行于轴的直线MN与EB交于点M．现将纸片折叠，使顶点C落在MN上，并与MN上的点G重合，折痕为EF，点F为折痕与y轴的交点．

（1）求点G的坐标；

（2）求折痕EF所在直线的解析式；

（3）设点P为直线EF上的点，是否存在这样的点P，使得以P、F、G为顶点的三角形为等腰三角形，若存在，请直接写出点P的坐标；若不存在，请说明理由．

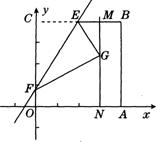
16．如图，已知，以点A为圆心，以AO长为半径的圆交轴于另一点B，过点B作BF∥AE交⊙A于点F，直线FE交x轴于点C．

（1）求证：直线FC是⊙a的切线；

（2）求点C的坐标及直线FC的解析式；

（3）有一个半径与⊙A的半径相等，且圆心在轴上运动的⊙P．若⊙P与直线FC相交于M，N两点，是否存在这样的点P，使△PMN是直角三角形．若存在，求出点P的坐标；若不存在，请说明理由．

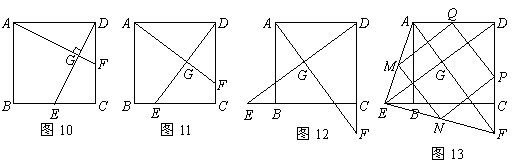
17．如图10，在正方形ABCD中，点E,F分别为边BC,CD的中点，AF,DE相交于点G，则可得结论：①AF=DE；②AF⊥DE．（不需要证明）

（1）如图11，若点E，F不是正方形ABCD的边BC，CD的中点，但满足CE=DF，则上面的结论①，②是否仍然成立？（请直接回答“成立”或“不成立”）

（2）如图12，若点E，F分别在正方形ABCD的边CB的延长线和DC的延长线上，且CE=DF，此时上面的结论1，2是否仍然成立？若成立，请写出证明过程，若不成立，请说明理由．

（3）如图13，在（2）的基础上，连接AE和EF，若点M，N，P，Q分别为AE，EF，FD，AD的中点，请判断四边形MNPQ是“矩形、菱形、正方形、等腰梯形”中的哪一种？并写出证明过程．

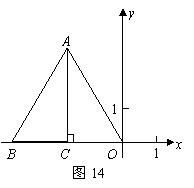
18．如图14，在平面直角坐标系中，两个全等的直角三角形的直角顶点及一条直角边重合，点在第二象限内，点B，点C在x轴的负半轴上，∠CAO=30°OA=4．

（1）求点C的坐标；

（2）如图15，将△ABC绕点C按顺时针方向旋转30°到△A’ CB’的位置，其中A’C交直线OA于点E，A’B’分别交直线OA,CA于点F,G，则除△A’B’C≌△AOC外，还有哪几对全等的三角形，请直接写出答案；（不再另外添加辅助线）

（3）在（2）的基础上，将A’CB’绕点C按顺时针方向继续旋转，当△COE的面积为时，求直线CE的函数表达式．
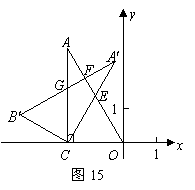