中考数学总复习专题训练（十二)　

 （圆）

考试时间：120分钟 满分150分

一、选择题（每小题3分，共45分）

1.如图1，点A、B、C在⊙O上，AO∥BC，∠OAC=20°，则∠AOB的度数是（　 ）。

A.1O°　　　 B.20°　　　C.40°　　　　D.70°

2.如图2，AB是⊙O的直径，BC、CD、DA是⊙O的弦，且BC = CD = DA．则∠BCD = （　 ）。

A．100°　　　 B．110°　　　C．120°　　　　 D．135°

3.如图3，AC是⊙O的直径，∠BAC=20°，P是弧AB的中点，则∠PAB=（　 ）。

A．35°　　　　 B．40°　　　 Ｃ．60°　　　　 D.70°

　　　　　　　　　　　

图1　　　　　　　  图2　　　　　　　　  图3　　

4.如图4中的度数是（　 ）。

　Ａ．55⁰　　　　B．110⁰　　 　　Ｃ．125⁰　　 　Ｄ．150⁰

5．如图5，CD切⊙O于B，CO的延长线交⊙O于A，若∠C=36°，则

∠ABD的度数是（　 ）。

Ａ．72°　　  　B．63°　　　　Ｃ．54°　　　 Ｄ．36°

图4　　　　　　　　　　　　　  图5

6．某同学制做了三个半径分别为1、2、3的圆，在某一平面内，让它们两两外切，该同学把此时三个圆的圆心用线连接成三角形.你认为该三角形的形状为（　 ）。

Ａ．钝角三角形　　B．等边三角形　 Ｃ．直角三角形　Ｄ．等腰三角形

7．在半径为1的⊙O中，弦AB、AC分别是、，则∠BAC的度数为（　 ）。

Ａ．15°　 　　B．15°或75°　　Ｃ．75°　 　　Ｄ．15°或65°

8．已知两圆的半径为3 cm和1 cm，一条外公切线长为4 cm，那么这两圆的位置半径为（　 ）

Ａ．内切　　　 B．相交　 　　　　Ｃ．外离　　　Ｄ．外切

9.已知圆锥侧面展开图的圆心角为90°，则该圆锥的底面半径与母线长的比为（　 ）。

A．　1∶2　　　　 B．　2∶1　　　　C．　1∶4　　　　D．4∶1

10.用一种如下形状的地砖，不能把地面铺成既无缝隙又不重叠的是（　 ）。

A．正三角形　　 　B．正方形　　 Ｃ．长方形　　 Ｄ．正五边形

11．边长为2的等边三角形的外接圆的半径是（　 ）。

Ａ．　　　　　B．　　　　　Ｃ．2　　Ｄ．

12.圆内接四边形ABCD中，四个角的度数比可顺次为（　 ）。

Ａ．4：3：2：1　　B．4：3：1：2　Ｃ．4：2：3：1（D）4：1： 3：2

13．下列图形中一定有内切圆的四边形是（　 ）。

Ａ．梯形　 B．菱形　 Ｃ．矩形　 Ｄ．平行四边形

14.如图6所示，AB是⊙O的直径，弦AC、BD相交于E，则等于（　 ）。

Ａ．　 B．  Ｃ．　Ｄ．

15．如图7，AB是⊙O的直径，M是⊙O上一点，MN⊥AB，垂足为N，P、Q分别是AM、BM上一点（不与端点重合），如果∠MNP=∠MNQ，下面结论：①∠1=∠2；②∠P+∠Q=∠180°；③∠Q=∠PMN；④PM=QM；⑤MN²=PN·QN。其中正确的是（　 ）。

A．①②③　　B．①③⑤　　C．④⑤　　D．①②⑤

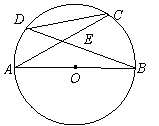
图6　　　　　　　　　  图7　

二、填空题（每小题3分，共30分）　　　

1．已知⊙O的半径为8, 圆心O到直线l的距离是6, 则直线l与⊙O的位置关系是_________。

2．如图8，DB切⊙O于点A，∠AOM=66°，则∠DAM=_________度。

3．已知：如图9，AB是⊙O的直径，弦EF⊥AB于点D，如果EF=8，AD=2，则⊙O半径的长是_________。

4．如图10，小明同学测量一个光盘的直径，他只有一把直尺和一块三角板，他将直尺、光盘和三角板如图放置于桌面上，并量出AB=3.5cm，则此光盘的直径是_________cm。

图8　　　　　　　  图9　　　　　　　　 图10　　

5．已知圆柱的底面半径为2cm，母线长为3cm，则该圆柱的侧面展开图的面

积为_________cm。

6．两圆外切，半径为4cm和9cm，则两圆的一条外公切线的长等于　　　　　　  。

7．已知扇形的圆心角为150°，弧长为20πcm，则扇形的面积为_________。

8．如图11，在以O为圆心的两个同心圆中，大圆的弦AB是小圆的切线，点P为切点，已知AB=8，大圆半径为5，则小圆半径为_________。

9．如图12：⊙O内切于弓形ADB的最大的圆，且弧ADB的度数为120°，则⊙O的周长与弧AB的长的比是　　　　　  。

10．如图13，已知圆柱体底面圆的半径为，高为2，AB、CD分别是两底面的直径，AD、BC是母线若一只小虫从A点出发，从侧面爬行到C点，则小虫爬行的最短D路线的长度是_____________。 (结果保留根式)

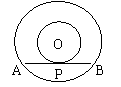
图11　　　　　　　　　 图12　　　　　　　　  图13　　

三、解答下列各题（第8题12分，其余每小题9分，共75分）

1．如图，PAB为⊙O的割线，PO交⊙O于C，OP＝13，PA＝9，AB＝7，求⊙O直径的长。

　

2．如图所示，PA、PB是⊙O的切线，A、B为切点，，点C是⊙O上不同于A、B的任意一点，求的度数。

3．如图，A、B、C、D是⊙O上的四点，AB=AC，AD交BC于点E，AE=2，ED=4，求AB的长。

4．如图，同心圆O，大圆的面积被小圆所平分，若大圆的弦AB，CD分别切小圆于E、F点，当大圆半径为R时，且AB∥CD，求阴影部分面积。

5．如图，AB是⊙O直径，EF切⊙O于C，AD⊥EF于D，求证：AC²=AD·AB。

6．如图，已知⊙O₁和⊙O₂相交于A，B，过A作直线分别交⊙O₁，⊙O₂于C，D，过B作直线分别交⊙O₁，⊙O₂于E，F，求证：CE∥DF

7．如图，在Rt△ABC中，∠B=90°，∠A的平分线交BC于D，E为AB上一点，DE=DC，以D为圆心，以DB的长为半径画圆。

求证：（1）AC是⊙D的切线；（2）AB+EB=AC。

8．如图，在Rt△ABC中，,BE平分∠ABC交AC于点E，点D在AB

上，。

（１）　 求证：AC是△BDE的外接圆的切线；

（２）若，求EC的长。

参考答案

一、1、C　　2、C　　 3、A　 4、D　 5．D　6、B　　7．B　 8．C　

 9、C　 10、D　 11、D　 12、B　 13、B　　14、C　15、B

二、1、相交　 2、147　3、5　4、　　5、12π；6、12cm；　

7、240πcm²；　　8、3；9、；10、。

三、1、5；2、连接OA、OB，在AB弧上任取一点C，∵PA、PB是⊙O的切线，A、B为切点，连接AC、BC，∴，

∵，在四边形OAPB中，可得。

①　　 若C点在劣弧AB上，则；

②　　 若C点在优弧AB上，则。　　　

3、AB=2。4、；5、提示：连接BC；6、提示：连接AB；

7、证明：（1）过点D作DF⊥AC于F.

∵AB为⊙D的切线,  AD平分∠BAC,  ∴BD=DF .

∴AC为⊙D的切线 .

　 （2）在△BDE和△DCF中,　∵BD=DF,　DE=DC,

∴△BDE≌△DCF（HL）,　∴EB=FC .

又AB=AF,　∴AB+EB=AF+FC,　即AB+EB=AC .

8、（1）取BD的中点O，连接OE。

∵BE平分∠ABC，∴∠CBE=∠OBE。又∵OB=OE，∴∠OBE=∠BEO，∴∠CBE=∠BEO，∴BC∥OE。∵∠C=90°，∴OE⊥AC，∴AC是△BDE的外接圆的切线。

（2）设⊙O的半径为r，则在△AOE中，

，即，解得,

∴OA=2OE，

∴∠A=30°，∠AOE=60°。

∴∠CBE=∠OBE=30°。

∴EC=。