中考数学模拟试题3

一、选择题（请选出各题中一个符合题意的正确选项，不选、错选、多选均不给分。本题有12小题，每小题4分，共48分）

1．计算（＋2）＋（－3）其结果是(　　　)

　　　A．＋1　　B．－1　　C．＋6　　D，－6

2．2001年温州市财政总收入为961088万元，用四舍五入法取近似值，保留三个有效数字，并用科学记数法表示其结果是(　　　)

A．9．61×10³万元　 B．9．61×10⁴万元　

C．9．61×10⁵万元　 D．9．610×10⁴万元

3．如图，立方体 ABCD—A₁B₁C₁D₁中，与棱AD垂直的平面是(　　  )

　　　A．平面A₁B，平面CD₁　　　B．平面A₁D，平面BC₁

　　　C．平面AC，平面A₁C₁　　　D．平面BD，平面AD₁

4．已知扇形的弧长是2πcm，半径为12cm，则这个扇形的圆心角是(　　　)

　　　A．60°　　B．45°　C．30°　　D．20°

5．圆锥的高线长是8㎝，底面直径为12㎝，则这个圆锥的侧面积是(　　　)

　　　A．48πcm²　　 B．24cm²　　　C．48cm²　　 D．60πcm²

6．不等式组　　　的解是(　　  )

　　　A．x＞2 　 B．x≥－2 　 C．x＜2 　　　 D．－2≤x＜2

7．若a＜0，化简其结果是(　　  )

　　　A．0　　　B．2a　C．－2a　D．2a或－2a

8．两圆的半径分别为3cm和4cm，圆心距为1cm，则两圆的位置关系是(　　　)

　　　A．相离　　 B．相交　　　　 C．内切　　　　D．外切　　

9．如图，AB是⊙O的直径，点 P在 BA的延长线上，PC是⊙O的切线 ，C为切点，PC＝2，PA＝4，则⊙O的半径等于(　　　)

　　　 A．1　B．2　　 C．　　D．

10．在△ABC中，点D、E分别在边AB，AC上，且DE∥BC，AE＝3，EC＝2，那么S_△ADE：S_△ABC等于(　　　)

　 A．2：3　　B．3：5　 C　9：4　　　D　9：25

11．一次抽奖活动中，印发奖券1000张，其中一等奖20张，二等奖80张，三等奖200张，那么第一位抽奖者（仅买一张奖券）中奖的概率是(　　　)

　　　　A．　　　　　B．　 C．　 D．

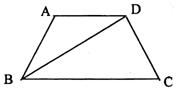12．如图，在梯形ABCD中，AD∥BC，AB＝DC，∠C＝60°，BD平分∠ABC，如果这个梯形的周长为30，则AB的长是(　　  )

　　　　  A．4　　　　　B．5　　　　  C．6　　　　　D．7

二、填空题（本题有6小题，每小题5分，共30分）

13．分解因式：x³一xy²－x＋y＝　　　　　　　 

14．已知　 y与x＋l成正比例，当x=5时,y＝12，则y关于x的函数解析式是　　  　

15．某养鱼户去年在鱼塘中投放了一批鱼苗，现在为了解这批鱼的平均重量，从中捞取10条鱼，测得其重量如下（单位：kg）

　　 1.2　1．1　0．9　0．8　　l．3　　1．2　1．3　1．0　1．0　1．2

　　试估计这批鱼的平均重量约是　　　　kg．

16．Rt△ABC中，∠C＝Rt∠，BC＝4，AB＝5，则tgB＝　　　　

17．某公司董事会拨出总题为40万元款项作为奖励金，全部用于奖励本年度做出突出贡献的一、二、三等奖的职工．原来设定：一等奖每人5万元，二等奖每人3万元，三等奖每人2万元；后因考虑到一等奖的职工科技创新已给公司带来巨大的经济效益，现在改为：一等奖每人15万元二等奖每人4方元，三等奖每人1万元，那么该公司本年度获得一、二、三等奖的职工共　　　　人．

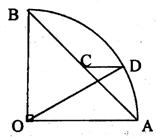
18．如图，扇形OAB中，∠AOB＝90°，半径OA＝1，C是线段AB的中点，CD∥OA，交弧AB于点 D，则CD＝　　　　

三、解答题（本题有4小题，共25分）

19．（本题6分）计算：

20．（本题6分）解方程组

21．（本题　6分）如图，△ACF内接于⊙O，AB是 ⊙O的直径，弦CD⊥AB于点E．

　 （1）求证：∠ACE＝∠AFC；

　 （2）若CD＝BE＝8，求sin∠AFC的值．

22．（本题7分）当m为何值时，方程x²－（m＋2）x＋m²＝0的两根之和与两根之积相等．

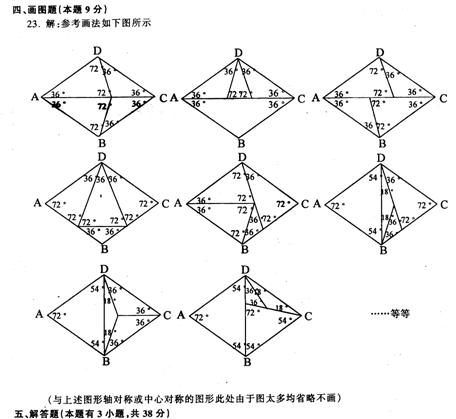
四、画图题（本题9分）

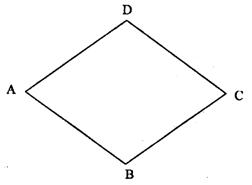
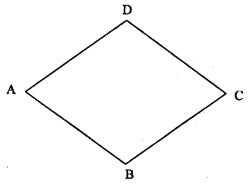
23．已知：菱形ABCD中（如图），∠A＝72°，请设计三种不同的分法，将菱形ABCD分割成四个三角形，使得每个三角形都是等腰三角形．（画图工具不限，要求画出分割线段；标出能够说明分法所得三角形内角的度数，没有标出能够说明分法所得三角形内角度数不给分；不要求写出画法，不要求证明．）

注：两种分法只要有一条分割线段位置不同，就认为是两种不同的分法．

分法一：　　　　　　　　　　　　　　　　分法二：

　　

分法三：

五、解答题（本题有3小题，共38分）

24．（本题12分）二次函数y=ax²+bx+c（其中a＞0)它的图象与x轴交于A（m,0),B（n,0)两点，其中m＜n，与y轴交于点C(0，t)

  (1）若它的图象的顶点为P，点P的坐标为(2,－1)，点C在x轴上方，且点C到x轴的距离为3，求A，B,C三点的坐标;(要求写出过程）

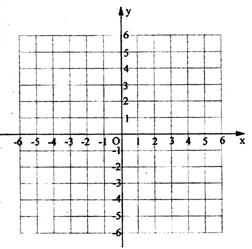
  （2）若m，n, t都是整数，且 0＜m＜6，0＜n＜6，0＜t≤6，△ABC的面积为6，试写出一个满足条件的二次函数的解析式　 　　　　　　　　  （只要求写出结果，不要求写出过程），并在直角坐标系中（下图），画出你所填二次函数的图象，且标出相应A，B，C三点的位置．

25．（本题12分）欣欣日用品零售商店，从某公司批发部每月按销售合同以批发单价每把8元购进雨伞（数量至少为100把），欣欣商店根据销售记录，这种雨伞以零售单价每把为14元出售时，月销售量为100把，如果零售单价每降价0．1元，月销售量就要增加5把．现在该公司的批发部为了扩大这种雨伞的销售量，给零售商制定如下优惠措施：如果零售商每月从批发部购进雨伞的数量超过100把，其超过100把的部份每把按原批发单价九五折(即95%）付费，但零售单价每把不能低于10元．欣欣日用品零售商店应将这种雨伞的零售单价定为每把多少元出售时，才能使这种雨伞的月销售利润最大？最大月销售利润是多少元？ （销售利润＝销售款额－进货款额）

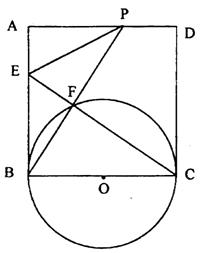26．（本题14分）如图，正方形ABCD中，AB＝l，BC为⊙O的直径，设AD边上有一动点P（不运动至A、D），BP交⊙O于点F，CF的延长线交AB于点E，连结PE．

　 （1）设BP＝x，CF＝y，求y与x之间的函数关系式，并写出自变量x的取值范围；

　 （2）当CF＝2EF时，求BP的长；

　 （3）是否存在点P，使ΔAEP∽ΔBEC（其对应关系只能是A—B，E－E，P－C）？如果存在，试求出AP的长；如果不存在，请说明理由．

　 数学参考答案

一、选择题(每小题4分，共48分)

题 号	1	2	3	4	5	6	7	8	9	10	11	12
答 案	B	C	A	C	D	A	C	C	A	D	D	C
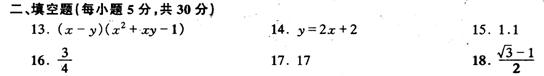