中考数学期末复习测试

数学试卷

一、选择题：（每题3分，共30分）

1.下列各式中正确的是(　 )

A. x²y⁵÷=xy⁴　　B.()^-1-()^-1=-

C.a⁰=1　　　　　　　　 D.-2^-2=-

2.如果“a+b+c=0 ,则a(+)+b(+)+c(+)的值为（　 ）

A. 　　 B.3　　C.-3　　 D.-

3.某商品连续两次降价10%后的价格为a元,则该商品的原价为(　 )

A. 　　　B.1.1²a　　　C.0.9²a　　D.

4.下列一元二次方程中，两个实数根的和为3的方程是（　 ）

A．x²-3x+4=0　　B.x²+3x+4=0　　C.x²-3x-4=0　 D.x²+3x-4=0

5.如果抛物线y=ax²+bx+c 过二、三、四象限，则a,b,c的符号为（　 ）

A.a>0 ,b>0,c>0　 B.a<0,b<0,c>0

C.a<0,b>0,c<0　　D.a<0,b<0,c<0

6.将二次函数y=2x²-4x+4的图象向右平移1个单位,再向下平移2个单位得到的新的二次函数为(　　)

A.y=2(x-1)²+4　　 B.y=2(x-2)²

C.y=2(x-2)²+4　　 D.y=2(x-1)²

7.一个点到圆的最小距离为4cm,最大距离为9cm,则该圆的半径是(　 )

A.2.5cm或6.5cm　 B.2.5cm　　C.6.5cm　　　D.5cm或13cm

8.已知⊙0的半径为γ,那么垂直平分半径的弦长是(　 )

A.γ　B.γ　 C. 2γ　 D. 4γ　

9.已知△ABC的内切圆分别切三边于点D、E、F，则以D、E、F三点为顶点的三角形一定是（　　 ）

A.锐角三角形　　 B直角三角形　　 C钝角三角形　　D无法确定

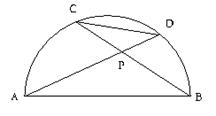10.如图AB为半圆0的直径,弦AD、BC相交于点P，若CD=3，AB=4，则tan∠BPD等于（　　）

A.　　 B.　　 C.　　D.

二、填空题（每题2分，共20分）

1.一种细菌的直径是0.米,用科学记数法表示为　　米.

2.化简:x+1-=　　

3.当a=　　 时方程=-2会产生增根

4方程x²=5的解是　　

5抛物线y=x²-2有最小值应该是　　

6若在⊙0中,如果AB=2CD则

AB　　 2CD(填“>=<”)

7圆的弦长等于半径,则这条弦的所对圆周角是　　

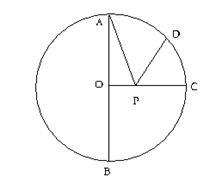
8如图AB是⊙0的直径;AB=2,OC是⊙0的半径,OC⊥AB,点D在AC上,AD=2CD,点P是半径OC上一个动点,则AP+PD的最小值等于　　　　

 

9已知x, x₂是关于x的方程x²-2x+t+2=0的两个不相等的实数根.设S=x₁²+x₂²,则S关于t的函数关系式为　　　　　  

10.我国股市交易中,每买卖一次都要交纳千分之七点五的各种费用,某投资商以每股10元的价格购入上海某股票1000股,当该股票涨到12元的时候全部卖出,该投资者实际盈利为　　　 元.

三、简答题

1.化简求值,已知a²-3a+1=0,求()·÷(a-3)的值(4分)

2.已知关于x的方程有一个正数解,求m的范围(4分)

3.已知关于x的方程x²-(k+2)x+2k=0

求证:①无论K取任何实数时,此方程必有实数根

②若等腰三角形的边长为a=1,另两边长b,c恰好是这个方程的两个根,求△ABC的周长(6分)

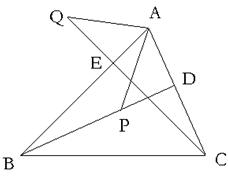
4.如图在△ABC,中,CE、BD分别是AB、AC边上的高，在BD上取一点P，使BP=AC；在CE的延长线上取一点Q，使得CQ=AB，连结AP、AQ，那么AQ和AP有什么关系？并说明你的结论（7分）

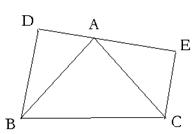
5.如图∠BAC=90°,AB=AC,BD⊥DE,CE⊥DE,垂足分别是D、E，求证：DE=BD（7分）

6、现定义两种运算 “⊕”，“⊙”：对于任意两个整数a , b ，

a⊕b = a + b－1，a ⊙ b = a×b－1 ．

　 求 4 ⊙ [（6⊕8）⊕（3⊙5）] 的值 ．

7、AB是⊙O的直径，弦CD⊥AB于E，F是CD延长线上一点，AF交⊙O于G；如果AC = 8，AG = 6，DG = 3，试求DF的长 ．

8、已知抛物线 y = x ²－( m ² + 5 ) x + 2 m ² + 6 ;

　 ⑴ 求证：不论 m 取何值，抛物线与 x 轴必有两个交点，并且有一个交点是A ( 2 , 0 ) ；

　 ⑵ 设抛物线与x轴另一交点为B，AB = d ，求 d 与 m之间的函数关系式 ；

　 ⑶ 设d = 10 ，P ( a , b ) 为抛物线上一点，且△ABP为锐角三角形，求b的取值范围 ．