中考数学辅导之—锐角三角函数和函数的图像

一、学习目标：

（一）1.理解锐角三角函数定义,会用锐角三角形定义列出函数关系式解直角三角形.

　 2.了解锐角三角函数的四个同角间的函数恒等式,并会解一些相关的题目.

　 3.理解锐角三角函数的性质,会比较在某个范围内正弦和正弦,正弦和余弦,　正切和正切,正切和余切的大小,及利用函数值的大小判断角的大小.

　 4.熟记特殊角的三角函数组,并会准确的计算.

　 5.会用解直角三角形的有关知识,解某些实际问题.

（二）1.了解平面直角坐标系的有关概念,会由点的位置确定点的坐标,会由点的　　　坐标确定点的位置.

　 2.理解函数的意义,能根据一个具体的函数解析式,确定自变量的取值范围,　并会由自变量的值求出函数值.

　 3.掌握正比例函数、反比例函数、一次函数、二次函数的概念及性质,会画出  图象.

　 4.能根据不同条件,用待定系数法求函数解析式.

二、基础知识及需说明的问题：

　　1.利用直角三角形边角之间的关系来解直角三角形,最主要的是记住定义。譬如说,我们要求直角三角形中一个锐角的度数,需根据已知条件是这个角的哪些边来选择函数定义,若已知直角三边形的一个锐角和一边长求另一边长也是如此.

2.正弦、正切函数都是增函数。即当角度在0⁰-- 90⁰间变化时，正弦、正切值随着角度的增大而增大。如：化简,我们先将此式由性质化简,然后看是大还是大.不妨在中取,则,_{（化成同名三角函数）}∵,∴_，这说明,_.∴_{（负数的绝对值是其相反数）。再如:已知，}确定角_的取值范围。∵,∴,因为余弦函数是随着角度的增大余弦值反而越小，∴.

3.在直角坐标系中,某个点的横坐标是该点向轴做垂线,垂足在轴所表示的那个实数,纵坐标是该点向轴作垂线,垂足在轴上表示的实数.点在轴上,纵坐标为0,即(,0).点在轴上,横坐标为0,即(0,).若两点关于轴对称, 则横坐标相同,纵坐标互为相反数. 若两点关于轴对称, 则纵坐标相同,横坐标互为相反. 若两点关于原点对称,则横坐标、纵坐标都互为相反数.

4.要注意结合图象理解：正比例函数、反比例函数、一次函数和二次函数的性质,要理解中的的正、负,知道图象在第几象限,的增大而增大还是减小.在中,要由的符号画出图象草图.知道的图象的位置,反之由在坐标系中的位置确定的符号,在二次函数 中知道的正、负确定开口方向,的正、负,确定抛物线在坐标系中的大体位置.

5.特别要注意：一次函数和二次函数轴交点的坐标的求法,即点在,此时，它们与轴交点的纵坐标都为零,而横坐标是上述方程的根.二次函数中的的值,决定着抛物线与轴交点的个数.时有两个交点; 时只有一个交点; 时没有交点。会利用求，并得出图象与轴的交点的坐标.

6.用待定系数法确定函数解析式是较难的.要总结经验归纳类型.

三、本期练习

 (一)判断题

1.一次函数,则它的图象经过一,二,四象限(　 )

2.当(　 )

3.已知斜坡AB的坡度,则坡角的度数是60°(　 )

4.函数的图象的两支在第一,三象限,的增大而增大(　 )

5.已知点A(-4,3)和(-4,-3),则A,B关于轴对称(　 )

6.在Rt△ABC中,AD是斜边BC边上的高,若BC=6,DC=2,则(　 )

 (二)填空题:

1.在Rt△ABC中,∠C=Rt∠,AC=3,BC=4,则=_____.

2.若=_____.

3.在Rt△ABC中,∠C=90°,b=6,则c=_____.

_4.,则锐角=_____度.

5.在RtΔABC中,∠C=90°,AD平分∠BAC,若AC=12,AD=8,则BC=_____.

6.函数轴的交点A的坐标是_____,与轴的交点B的坐标是_____,S△AOB=_____.

7.在Rt△ABC中,∠C=90°,,斜边c=10,则Rt△ABC内切圆的半径是_____,内心与外心间的距离是_____.

8.函数的自变量的取值范围是_____.

9.抛物线轴只有一个交点,则_____.

10.抛物线的顶点关于轴的对称点的坐标是_____.

11.一次函数的图象经过(2,2)和(3,5)点,则函数解析式是_____.

12.的值是_____.

　13.如果的图象经过(1,4),(0,2)和(-2,-8)三点,则的值是_____.

14.已知的正比例函数,的反比例函数,且间的函数解析式是_____.

　15.已知直线交点的横坐标是1,与交点的纵坐标是4,则函数的解析式是_____.

　16.已知轴交点的纵坐标是2,它与两坐标围成的三角形的面积是7,则这个函数的解析式是_____.

　17.相交点C,设两直线与轴分别交于A,B,与轴交于P,Q,则点C的坐标是_____.S△ABC=_____,S△CPQ=_____.

　18.直线的交点坐标是C(3,-1),两直线与轴分别交A,B,且S△ABC=9,则直线的解析式是_____.

　19.二次函数的图象与轴交于A,B两点,(A在B的左边)与轴交于C,线段OA与OB的长的积等于6,(O是坐标原点),则m的值是_____,S△ABC=_____.

　(三)选择题:

1.若函数在同一坐标系中相交,且,则交点在:

A.第一象限　　B.第二象限　　C.第二,四象限　　D.第四象限

2.∠A是锐角,,则∠A:

　　A.<30°　　B.> 30°　　C.<60°　　D.>60°

3.在同一坐标系中,的图象大致是:

　　　　y　　　　　　　  y　　　　　　　 y　　　　　　　 y

　　　　0　　　　　　  　 0　　　　　　  0　　　　　　　 0

　　　　　　　 x　　　　　　　  x　　　　　　　 x　　　　　　　  x

　　　  A.　 　　　　　　B.　　　　 　　 C.　　　　　　 D.

　(四)解答题

　已知关于的二次函数 ，求：

　1.关于的一元二次方程的两根平方和等于9,求的值.

　2.在1的条件下,设这个二次函数的图象与轴从左到右交于A,B两点,问在对称轴的右边的图象上,是否存在点M,使锐角△AMB的面积等于3,若存在,请写出点M的坐标;若不存在,请说明理由.

四、本期练习答案

 (一)1.√  2.√  3.×  4.×  5.×  6.√

 (二)1. 　 2. 　 3. 　 4. 30° 5. 　 6. (9,0),(0,-3)　

7. 2; 　 8. 　 9. ¨5或3　 10. (3,-2)　 11.

　　12. 　13. 4　14. 　15.　　

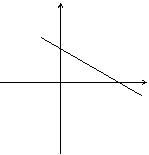16.提示:设轴交于(0,2)　　　　　　　　　  y

它与轴交于(),则S△AOB=　　　　　　  A(0,2)

　 

∴与轴交于(7,0)和(-7,0)　　　　　　　　　　　　　 0　B() x

将代入公式,

将代入得

17.交点C的坐标是 的解 　S△ABC=25　 S△CPQ=

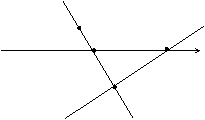
18.提示:轴交于(2,0),与轴交于()

则　　

∴B(20,0)或(-16,0)分别和C(3,-1)代入得

∴和　　y

　　　　　　　　　　　　　　　　　　　　　

 

　　　　　　　　　　　　　　　  0　A(2,0)　　 B(,0)

　　　　　　　　　　　　　　　　　　　  C(3,-1)

　　　　　　　　　　　　　　　　　　　 

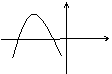19.二次函数轴交于A()和B(),是的根.线段OA的长是,线段OB的长是,由题意得:,若图象是

　　　　　　　　　 

　　　　　　　　　　　　　　　　 A()　　B()

则　　　两根之积是6

　　　　

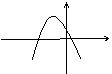若图象是

　　　　　　　　　 

　　　A()　　 B()

则　　　

　

∴　 S△ABC=3或15

　(三)1.D　2.C　3.C

　(四)①由　　得

　②∵　∴与轴交于A(0,0)和B(3,0)

　设存在

　由题意得　　

　将舍去(若点必在轴上方,此时△AB是钝角三角形,与△AB是锐角三角形不符)

当时,　　　　

∴　也会在[因为]在对称轴左边.

∴适合条件的点是(2,-2)　

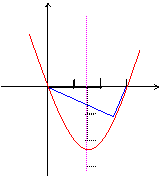　　　　　　　　　　　　  y　　

　　　　　　　　　　　　  A　　　　　 B