中考数学辅导之—一次函数的图象和性质

 

一次函数是本章中最重要的一个单元，在课本中，讲叙本部分内容的篇幅虽然不长，但利用它的概念、性质解决的题目却不少，而且有些题目还较难，并且从这部分内容开始，我们将学习利用代数的方法去解决几何问题，这是同学们过去从未涉及到的方法，所以不管从解题思路、解题方法上还是从所学知识的综合应用上的要求都有较大幅度的提高，可能会使同学们感到有时无从下手，“很难学”是同学们普遍的反映。在本讲中，我们将要补充一些必要的知识，讲解几个例题，以便使同学们体会解题思路和解题方法，从而达到较好的掌握本部分知识的目的。

一、学习要求：

1.理解一次函数和正比例函数的概念。

2.会画正比例函数及一次函数的图象。

3.理解并掌握正比例函数和一次函数的性质。

4.会利用待定系数法确定正比例及一次函数的解析式。

5.会解关于一次函数的较难的题目。

二、知识要点：

　　1.正比例函数和一次函数是分别用和来定义的，其中是自变量，是自变量的函数，k是自变量的系数，是常数，这两种函数解析式都是方程，而且它的图象上的点的坐标都是对应方程的解，因此，一次函数与一次方程有密不可分的关系。

　　2.课本中,用具体的函数利用描点法得出正比例函数和一次函数的图象都是一条直线，既然是一条直线，我们只要描出两点即可确定该直线。因为正比例函数是过原点的直线，当然坐标原点是所描的两点中的一个，另外一个是时y=k就是点，所以正比例函数的图像是过（0，0）、（1，k）两点的直线。而一次函数与两条坐标轴各有一个交点（注意：与x轴、y轴交点的坐标是极其重要的），那么“两点确定一条直线”中的两点就可以取这两个交点，由于一次函数与x轴的交点必在x轴上,而在x轴上的点的特点是纵坐标为0，即：在一次函数中，当y=0时可得kx+b=0，解此方程得x=-，从而得出一次函数与x轴交于（-，0）点；同理，由一次函数与y轴交点的横坐标为0可以得出：它与y轴的交点为（0，b）；因此一次函数的图象是过它与x轴的交点（-，0）和它与y轴的交点（0，b）两点的直线。（实践证明，很多同学不会求直线与轴的交点坐标，这是不会解一些一次函数题目的直接原因）。例如描述的图象：令,令,所以的图像是过轴上的（0，-5）和x轴上的（，0）两点的直线。

　　　　　　　　　　　　　　　　　　 x

　　　　　　　　　　　　　　　

　　　　　　　　　　　　　 A(0,5)

　　　　　　　　　　　　　

3.的图象的性质中的增大而增大，的增大而减少，此性质反映在图象上是时图象自左而右是“上升”的，如

反之，图象自左而右是上升的,则；图象自左而右是“下降”的，如

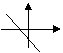
　　　　。由于与在轴的正半轴上，直线与

轴交于正半轴，在轴的负半轴，与轴交于负半轴。

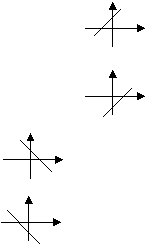　　　　　　　　　　　 　　　　　　　　　　　　　 y

①的图象在一、二、三象限　　 0　 x

　　　　　　　　　　　　　　　　　　　　　　　　　　  y

②的图象在一、三、四象限　 0　　x

　　　　　　　　　　　　　　　　　　　　　  y

③图象在一、二、四象限　 0　　 x

　　　　　　　　　　　　　　　　　　　　　 y

④图象在二、三、四象限　 0　　 x

4.如果在轴上有两个点，则A、B两点的距离是 x_2—x₁，如(-1，0)和(3，0)两点的距离就是3-(-1)=4，在轴上有两点A(0，y₁)和B(0，y ₂)，则A、B两点的距离是y₂-y₁，如(0，2)和(0，-5)的距离是-5-2=7。

5.两条直线的交点坐标是方程组 的解.如y=x-2和y=-3x+1的交点坐标就是方程组 的解 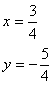即交点坐标是()。

6.利用待定系数法确定正比例函数和一次函数的解析式，一般步骤是:

①先设出函数的一般形式，如求正比例函数解析式时，先设，求一次函数的解析式时，先设。

②将自变量的值及与它对应的函数值的值代入所设的解析式，得到关于待定系数的方程或方程组。

③解方程或方程组，求出待定系数的值，进而写出函数解析式。

(注意：求正比例函数，只要一对的值就可以，因为它只有一个待定系数；而求一次函数则需要两组的值。）

三、例题:

例1:已知成正比例,且

(1)求间的函数解析式.

(2)求当.

(3)求当的值.

解:(1)∵成正比例

　　　∴

　　　　把代入上式得k=2

　　　∴

　　注意: [1]因为成正比例,把看成一个变量

　　　　  [2]成正比例,设.

(2)当.

(3)当.

例2:已知一次函数的图象经过(1,1)和(-1,-5)

求(1)此函数解析式.

　(2)求此函数与轴的交点坐标及它的图象与两坐标轴围成的三角形面积.

　(3)设另一条相干直线与此一次函数图象交于(-1,m)点,且与轴交点的纵坐标是4,求这条直线的解析式.

解:(1)设一次函数的解析式是

　　　将和代入得

　　　解得

　　　∴此一次函数解析式为

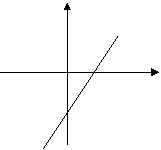　 (2)对,令则图象与A(0,-2)令,则此函数与轴交于B().　　　　  y

图象与两坐标轴围成的三角形面积　　　　　  O　　 B() x

是SΔAOB,其底长个单位,高-2=2　　　　　　 A(0,-2)　　

个单位.

∴SΔAOB=

(3)由于(-1,m)即在图象上,又在所求的另一条直线上,所以(-1,m)满足y=3x-2,将x=-1,y=m,代入y=3x-2得m=-5,所以两直线交于(-1,-5),说明第二条直线也经过(-1,-5)且还经过(0,4).

设另一条直线为y₁=k₁x+b,将x=-1,y=-5.x=0,y=4代入得

∴

∴第二条直线的解析式是y=9x+4.

例3:一次函数y=2x+3的图象与y轴交于A，另一个次函数图象与y轴交于B，两条直线交于C,C点的纵坐标是1,且SΔABC=16,求另一条直线的解析式.

解:∵y=2x-3与y轴交于A(0,-3)

设另一条直线的解析式是y=kx+b,则它与y轴交于B(0,b)

∵两直线交于C,C的纵坐标是1,设C(x,1)　　 y　　　y=2x-3

∴C在y=2x-3上

∴将y=1代入y=2x-3中得x=2　　　　　　　  B(0,b)

∴C的坐标是(2,1)

画草图分析　　　　　　　　　　　　　　　　　  C(2,1)

则ΔABC的底AB=b-(-3)=b+3　　　　　　　　　　　　 x

高是C点的横坐标2=2　　　　　　　　　　  A(0,-3)

由题意得　　　　　　　　　　　　　　　 y=kx+b

b+3=16

b+3=16或b=-19则函数解析式是y=kx+13或y=kx-19再将x=2,y=1代入得k=-6或k=10.

∴所求函数解析式为y=-6x+13或y=10x -19

(注意:画草图分析是非常必要的.否则此题的解题思路不会清楚).

四、练习题:

(1)填空题:

　1.函数的图象经过点(1,-3),则b=____,它的图象经过第____象限,随的增大而____.

　2.函数的图象经过点(-2,6),则它的图象经过第____象限,它的图象 象与交于____,与轴的交点坐标是____,它的图象与坐标轴围成的三角形面积是____.

　3.若一次函数图象过原点,则____.若图象与轴交于点(0,4),则=____.

　4.一次函数的图象与坐标轴围成的三角形的面积是9,则=____.

　5.已知一次函数的图象与轴交点A(a,0)和B(0,b),且a,b是方程.则该函数的解析式是____.

　6.已知:直线与直线,它们的交点C的坐标是____,设两直线与轴分别交于A,B,则SΔABC=____,设两直线与轴交于P,Q,则SΔPCQ=____

　7.一次函数与正比例函数的图象都经过(2,-1),则这两个函数的图象与轴围成的三角形面积是____.

(2)选择题:

1.若一次函数的图象经过一、二、三象限,则应满足的条件是:

A.　　B.　　C.　　D.

2.已知：是正比例函数,则的值是：

A.=1　　B. =-2　　C. =1或=-2　  D. 0

3.函数,如果,则的相应的取值范围:

A.　　B.　　C.　　D.

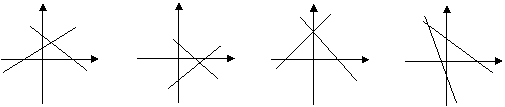
4.如图,两个一次函数,它们在同一直角坐标系中大致的图象是:

　　　　y　　　　　　　　 y　　　　　　　 y　　　　　　　  y

　　　　　  y₁　　　　 y₁　　　　　　　　　 y₂

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 

　　　0　　　 x　　　　0　　　x　　　　 0　　　x　　　　 0　 y₁ x

　　　　　  y­₂  y₂　　　　　　　　　　　  y₁　　　　  y₂

　　　 A.　　　　　　　 B.　　　　　　　 C.　　　　　　　 D.

  5.如果函数的图象与函数的图象和交于轴上的同一点,则等于:

　　A.　  B.2:3　　C.3:(-2)　　D.(-3):(-2)

(3)解答题:

　1.已知的图象与轴交于A,它与的图象交于C,C点的横坐标是与轴交于B,且SΔABC=,求函数的解析式.

　2.已知直线的图象经过点(1,6)和(-3,-2)它和轴,轴交点是B,A,直线的图象经过点(2,-2)且与轴交于(0,-3),它与轴,轴的交点是D,C.

求: (1)两直线的解析式.

　　(2)S_四边形ABCD

　　(3)若直线,求SΔBCE:S_四边形ABCD.

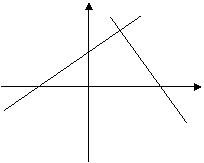
　3.如图,已知直线PA,与轴交于A,与轴交于Q,另一条直线轴交于B,而直线交于P

求: (1)A,B,Q,P四点的坐标(用或表示)

　　(2)若AB=2,且S_四边形PQOB=,求两个函数的解析式.

　　　　　　　　　　　  　　　　 y

　　　　　　　　　　　　　　　　　　  P

　　　　　　　　　　　　　　  Q

　　　　　　　　　　　　  A　　0　　　　  B　 x

五、练习答案:

(1)1.　-5, 一、三、四象限, 增大

　 2． 二、三、四象限,(-),(0,-4),

　 3.　3,-1或4

　 解题指导:直线与轴交于轴交于由题意,,解得

　5.

　6.SΔABC=25,SΔPCQ=.

　解题指导:由题意得C(7,10),A(2,0),B(-3,0),P(0,-4),Q(0,3),则AB=2-(-3)=5,高是C的纵坐标10.所以SΔABC=.

　7.　解题指导:将(2,-1)代入解得:,所以.轴交于A(),轴交于B(0,0).所以AB=,高是-1=1,所以SΔ

(2)选择题:

　1.A　　2.B　　3.B　　4.B　　5.C

(3)1.由题意得C(3,-1) A(4,0) 设B()

　　 　　　　

即B点坐标是(0,9)或(-1,0)

用(9,0)和(3,-1)两点求解析式

用(-1,0)和(3,-1)两点求解析式

　2.(1)

(2)由题意得B(-2,0),A(0,4),D(6,0),C(0,-3)

　 S_四边形ABCD=SΔABC+SΔADC

　 ∵A(0,4)　C(0,-3)

　 ∴AC=7

　　 SΔABC=

　　 SΔADC=

　 ∴S_四边形ABCD=28

(3)由题意得E　　　 SΔAEC=

　 SΔAEC=SΔAEC-SΔABC=-7=

　 ∴SΔBEC:S_四边形ABCD=

3.由题意得

　P点坐标是 的解，即P

　∵AB=2　　 

　∴　

　　SΔABP=

　　SΔAOQ=

　∴　　

　　　　 　　

　∴