中考数学辅导之—一元二次方程
本期我想将已学过的代数的第十二章《一元二次方程》来一次较系统的复习.
一、基础知识及说明的问题
1.一元二次方程：含有一个未知数,并且未知数最高次数是2的整式方程叫一元二次方程.其一般形式是ax2+bx+c=0(a≠0),在这个问题中注意三点:①会判断一个方程是不是一元二次方程;②能准确的将一个一元二次方程整理成一般形式,并准确的指出二次项系数,一次项系数和常数项;这一点是重要的.譬如用公式法解一元二次方程,若a,b,c不能确定,就不能准确的解方程.另外,根的判断式b2-4ac,一元二次方程根与系数之间的关系都是用a,b,c表示的;③要注意a≠0这一条件.
2.一元二次方程的解法:
①会用直接开平方将形如ax2=c(a,c同号)及(x+m)2=n(n≥0)的一元二次方程求解.
②会用配方法解一元二次方程,特别的是会用配方法解方程ax2+bx+c=0(a≠0)即会推导一元二次方程的求根公式.
③熟练,准确的利用公式法解一元二次方程,掌握此方法是关系.因为只要是一元二次方程,假设你不会直接开平方法,你也不会因式分解法,但只要掌握公式法,对于解方程来说就足够了.
④因式分解法,注意:一定要分解两个一次因式的乘积等于零的形式.如分解成(ax+b)(cx+d)=0,然后每个因式分别为零.
3.根的判别式:ax2+bx+c=0的b2-4ac.可以解决
①给定一个方程可判断方程根的情况.
如2x2-5x-1=0因为b2-4ac=(-5)2-4×2×(-1)=25+8=33>0可判断方程一定有两个不相等实根;
②利用题目给出的条件,求m或k的取值范围.
如关于x的方程(k-1)x2+3x-1=0有实根,求k的值.
解:Δ=b2-4ac=32-4(k-1)(-1)=9+4k-4=4k+5
因为方程有实根4k+5≥0,(建立起了关于k的不等式)k≥
当k≥且k≠1时,方程有实根.
③证明方程根的情况.
如证明方程4x2+(4+k)x+k=0必有实根
证明:Δ=(4+k)2-4×4×k=k2+8k+16-16k
=k2-8k+16
=(k-4)2
不论k取何实数(k-4)2≥0,即Δ≥0.
即证明方程必有实根.
要通过对比分析出与②中的题目的思路,方法,格式的不同,即②中的例题的题设是方程有实根,结论是m取何值.③中的例题是条件是k取任何实数,结论是有实根.
4.一元二次方程的根与系数之间的关系.
设x1,x2是ax2+bx+c=0(a≠)的两根,
则
,它的应用有:
①已知方程的一个根,求另一根及k(或m)的值.
如已知
是x2+kx+2=0的一个根,求另一根k的值.
解:设另一根是x,则由题意得
① 
② 
代入①式得
∴k=-4
∴k的值是-4,另一根是.
②利用根与系数的关系求某些代数式的值.
如已知x1,x2是方程2x2-3x-1=0的根.
求
的值.
此类题目是一元二次方程根与系数间的关系应用的基础,充分利用
,这就要将这些代数式变形成能用的形式.
如将
③求某些字母的值.
如已知x1,x2是2x2-mx-30=0的根,且5x1+3x2=0,求m的值.
解:由一元二次方程根与系数间的关系
① 
②
由
代入①式得:
∴
将
代入②式得:
④建立方程.
以x1,x2为根的方程是x2-(x1+x2)x+x1x2=0.要求熟记此公式.
若要以
为根作一个方程就是
.
要以
为根作一个方程就是
.
如已知方程2x2-5x-3=0
求作一个新的方程,使它的根分别是原方程根的①平方;②相反数;③3倍.
解:设x1,x2是2x2-5x-3=0的根
则
①所求方程是
即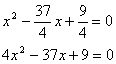
②所求方程是
即
③所求方程是
即
⑤杂题.如已知方程
m为何值两根互为相反数(x1+x2=0,Δ>0)
m为可值两根互为例数(x1·x2=1,Δ>0)
5.二次三项式ax2+bx+c的因式分解
若x1,x2是ax2+bx+c=0的根
则ax2+bx+c=a(x-x1)(x-x2)
注意问题:①因式分解要记作分解公式
②令ax2+bx+c=0求根
(若Δ<0,方程无实根,说明不能在实数范围内分解)
6.一元二次方程的应用,一般分三种类型的题目
①如两个连续偶数之积是168,求这两个数;
②面积问题.
如利用墙的一边,以长为28米的铁丝
网围成一个面积是96m2的矩形养鸡场,墙的
长度是15米,求鸡场的长和宽.
解:设宽为x米,则长是(28-2x)米
由题意得:x(28-2x)=96 2x2-28x+96=0
x2-14x+48=0 x1=6 x2=8
但x=6不合题意,(因为若宽为6米,则长是16米,长于墙的长度不行.)
28-2x=12
答:鸡场的长12米,宽8米.
③百分率问题.
原数(1+增长率)n=增长到的数 (n是连续增长次数,设每一次增长率相同)
例1. 某厂一月份销售额20万元,到三月份销售额达到26.45万元,求每月的增长率.
解:设增长率是x
由题意得20(1+x)2=26.45
例2. 某印刷厂一月份印书50万册.第一季度共印刷了182万册,求每月的增长率.
注意此题和例1不同,182万是1月印数+2月印数+3月印数=182
一月份50 二月份50(1+x) 三月份50(1+x)2
∴50+50(1+x)+50(1+x)2=182
因复习讲稿篇幅过长,望同学们很好看讲稿,关于综合复习题,我们将在10月底提供给大家.