中考数学辅导之—正多边形和圆及正多边形的有关计算
正多边形和圆是初中几何课本中的最后一单元,它包括正多边形的定义、正多边形的判定、性质,正多边形的有关计算,圆周长及弧长公式,圆、扇形、弓形的面积。今天我们一起学习正多边形的定义、判定、性质及有关计算.
一、基础知识及其说明:
1.正多边形的定义:各边相等、各角也相等的多边形叫做正多边形.此定义中的条件各边相等,各角也相等 “缺一不可”.如:菱形各边相等,因四个角不等,所以菱形不一定是正多边形.矩形的四个角相等,但因四条边不一定相等,故矩形不一定是正四边形,只有正方形是正四边形.
2.正多边形的判定,正多边形的定义当然是正多边形的判定方法之一,但如同全等三角形的判定一样,用定义来证明两个三角形全等显然不可取,因此需用判定定理来证.
判定定理:把圆几等分(![]() )
)
①依次连结各分点所得的多边形是这个圆的内接正![]() 边形
边形
![]() ②经过各分点做圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正
②经过各分点做圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正![]() 边形.也就是说,若要证明一个多边形是圆内接正多边形,只要证明这个多边形的顶点是圆的等分点即可, 如:要证明一个圆内接
边形.也就是说,若要证明一个多边形是圆内接正多边形,只要证明这个多边形的顶点是圆的等分点即可, 如:要证明一个圆内接![]() 边形ABCDEF……是圆内接正
边形ABCDEF……是圆内接正![]() 边形,就要证A、B、C、D、E、F……各点是圆的n等分点,就是要证AB=BC=CD=DE=EF=…….同样,要证明一个圆外切
边形,就要证A、B、C、D、E、F……各点是圆的n等分点,就是要证AB=BC=CD=DE=EF=…….同样,要证明一个圆外切![]() 边形是圆外切正
边形是圆外切正![]() 边形,只要证明各切点是圆的等分点即可.
边形,只要证明各切点是圆的等分点即可.
例1:证明:各边相等的圆内接多边形是正多边形.
已知:在⊙O中,多边形ABCDE……
是⊙O的内接n边形, O E
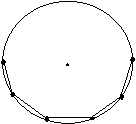 且AB=BC=CD=DE=…….
且AB=BC=CD=DE=…….
求证:n边形ABCDE……是正n边形. A D
证明: AB=BC=CD=DE=…… B C
![]() ∴ AB=BC=CD=DE……
∴ AB=BC=CD=DE……
![]() ∴OEB=AEC= BED=COE=……
∴OEB=AEC= BED=COE=……
∴![]()
又∵AB=BC=CD=DE=……
∴n边形ABCDE……是正n边形.
例2:证明:各角相等的圆外切n边形是正n边形.
已知:多边形![]() ……是圆外切n边形,切点分别是A,B,C,D,E……,
……是圆外切n边形,切点分别是A,B,C,D,E……,![]() =…….
=…….
求证:n边形![]() ……是正n边形.
……是正n边形.
证明:连结OB,OC,OD……,在四边形COD![]() 和四边形BOC
和四边形BOC![]() 中
中
∵![]() 切⊙O于B,C,D
切⊙O于B,C,D
∴![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ∴
∴ ![]() A
F
A
F
而![]() ……
……
![]()
![]()
![]() ∴
∴![]()
∴BC=CD(在同圆中,相等的圆
B
O ![]()
心角所对的弧相等).
![]()
![]()
![]() 同理BC=CD=DE=FE=……
同理BC=CD=DE=FE=……
![]() D
D
∴A,B,C,D,E,F……是圆的n等分点 C
∴多边形ABCDEF……是圆外切n正多边形
![]()
3.正多边都是轴对称图形,若n是奇数,正n边形是轴对称图形,n是偶数,正n边形既是轴对称图形又是中心图形.
4.正多边形的性质:任何正多边形都有一个外接圆和一个内切圆,这两个圆是同心圆.
5.正多边形的外接圆(或内切圆)的圆心叫正多边形的中心.外接圆半径叫正多边形的半径.内切圆的半径叫正多边形的边心距.正多边形的每一边所对的圆心角叫中心角,中心角的度数是![]() .
.
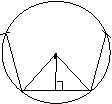
如图:OA,OB是半径,O是中心,
OH⊥AB于H,OH是边心距,![]()
是中心角. O
A H B
6.正多边形的有关计算,一般是围绕正![]() 边形的半径R,边长
边形的半径R,边长![]() ,边心距
,边心距![]() ,周长
,周长![]() 及面积
及面积![]() 来进行,但关健是
来进行,但关健是![]() 之间的计算,因为正
之间的计算,因为正![]() 边形的边心距把正
边形的边心距把正![]() 边形的一边与该边所对应的两条半径所围成的等腰三角形分成两个全等的直角三角形,所以在Rt△AOH中,斜边是R,直角边分别是
边形的一边与该边所对应的两条半径所围成的等腰三角形分成两个全等的直角三角形,所以在Rt△AOH中,斜边是R,直角边分别是![]() 和
和![]() ,锐角
,锐角![]() ,利用直角三角形的有关知识(勾股定理,锐角三角函数等)来解直角三角形即可.
,利用直角三角形的有关知识(勾股定理,锐角三角函数等)来解直角三角形即可.
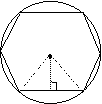
例:已知正六边形ABCDEF的半径是R,求正六边形的边长![]() S6.
S6.
解:作半径OA、OB,过O做OH⊥AB,
则∠AOH=![]() =30°
=30°
 ∵
∵![]() E
D
E
D
∴![]() F
O C
F
O C
∴![]() ∴
∴![]()
A H B
∵![]()
∴![]()
S6=![]()
同学们在进行正多边形的计算时,应很好的理解、掌握如何用解直角三角形的方法进行计算,但也可以推出公式,然后利用公式变形进行计算.
![]()
则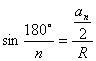 O
O
![]() A H B
A H B
![]()
这是已知半径R,求![]() 的公式,若记住公式则正多边形的计算就简单了很多,如已知半径R,求
的公式,若记住公式则正多边形的计算就简单了很多,如已知半径R,求![]()
解:![]()
![]()
再如:已知正三角形的边长为![]() ,可以先由
,可以先由![]() ,求出半径
,求出半径![]() ,再将求得的R代入
,再将求得的R代入![]() ;若已知边心距求边长,则先用
;若已知边心距求边长,则先用![]() ,求出R,再代入求边长公式
,求出R,再代入求边长公式![]() 即可求出,此法好处是不用画图,只需将上面两个公式反复变形即可.
即可求出,此法好处是不用画图,只需将上面两个公式反复变形即可.
7.如何求同圆的圆内接正![]() 边形与圆外切正
边形与圆外切正![]() 边形的边长比,半径比,边心距比.如:求同圆的圆内接正
边形的边长比,半径比,边心距比.如:求同圆的圆内接正![]() 边形和圆外切正
边形和圆外切正![]() 边形的边长比.
边形的边长比.
设⊙O的半径的为R
则圆内接正![]() 边形的边长是
边形的边长是![]()
 O
O
A D
B H
C
而在Rt△OBC中,OB=R,则![]() ,
,![]() 即外切正
即外切正![]() 边形的边长是
边形的边长是![]() ,
,
∴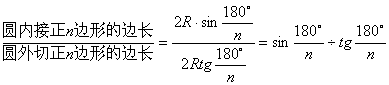
=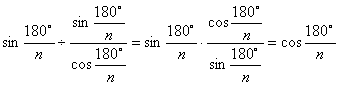
实际上,![]()
=![]() ,OB是
,OB是![]() 的邻边,OC是Rt△BOC的斜边,
的邻边,OC是Rt△BOC的斜边,![]() ,希望同学们记住此结论.如圆内接正四边形的边心距与圆外切正四边形的边心距之比是
,希望同学们记住此结论.如圆内接正四边形的边心距与圆外切正四边形的边心距之比是![]() ,圆内接正六边形与圆外切正六边形的边长之比是
,圆内接正六边形与圆外切正六边形的边长之比是![]() ,而圆内接正三角形与圆外切正三角形的面积之比是
,而圆内接正三角形与圆外切正三角形的面积之比是![]() .(注意:①此结论必须是同圆的边数相同的圆内接正
.(注意:①此结论必须是同圆的边数相同的圆内接正![]() 边形与圆外切正
边形与圆外切正![]() 边形的相似比是
边形的相似比是![]() .②若求圆外切正
.②若求圆外切正![]() 边形与圆内接正
边形与圆内接正![]() 边形的相似比则是
边形的相似比则是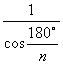 ).
).
二、练习题:
1.判断题:
①各边相等的圆外切多边形一定是正多边形.( )
②各角相等的圆内接多边形一定是正多边形.( )
③正多边形的中心角等于它的每一个外角.( )
④若一个正多边形的每一个内角是150°,则这个正多边形是正十二边形.( )
⑤各角相等的圆外切多边形是正多边形.( )
2.填空题:
①一个外角等于它的一个内角的正多边形是正____边形.
②正八边形的中心角的度数为____,每一个内角度数为____,每一个外角度数为____.
③边长为6cm的正三角形的半径是____cm,边心距是____cm,面积是____cm.
④面积等于![]() cm2的正六边形的周长是____.
cm2的正六边形的周长是____.
⑤同圆的内接正三角形与外切正三角形的边长之比是____.
⑥正多边形的面积是240cm2,周长是60cm2,则边心距是____cm.
⑦正六边形的两对边之间的距离是12cm,则边长是____cm.
⑧同圆的外切正四边形与内接正四边形的边心距之比是____.
⑨同圆的内接正三角形的边心距与正六边形的边心距之比是____.
3.选择题:
①下列命题中,假命题的是( )
A.各边相等的圆内接多边形是正多边形.
B.正多边形的任意两个角的平分线如果相交,则交点为正多边形的中心.
C.正多边形的任意两条边的中垂线如果相交,则交点是正多边形的中心.
D.一个外角小于一个内角的正多边形一定是正五边形.
②若一个正多边形的一个外角大于它的一个内角,则它的边数是( )
A.3 B.4 C.5 D.不能确定
③同圆的内接正四边形与外切正四边形的面积之比是( )
A.1:![]() B.1:
B.1:![]() C.1:2 D.
C.1:2 D.![]() :1
:1
④正六边形的两条平行边间距离是1,则边长是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
⑤周长相等的正三角形、正四边形、正六边形的面积S3、S4、S6之间的大小关系是:( )
A.S3>S4>S6 B.S6>S4>S3 C.S6>S3>S4 D.S4>S6>S3
⑥正三角形的边心距、半径和高的比是( )
A.1:2:3 B.1:![]() :
:![]() C.1:
C.1:![]() :3
D.1:2:
:3
D.1:2:![]()
三、练习答案:
1.判断题 ①× ②× ③√ ④√ ⑤√
2.填空题
①四
②45°,135°,45°
③![]() ④12
④12
⑤1:2
1:4 ⑥8 ⑦![]() ⑧
⑧![]() :1 ⑨1:
:1 ⑨1:![]()
3.选择题 ①D ②A ③C ④C ⑤B ⑥A