《圆》基础测试

（一）选择题（每题2分，共20分）

1．有下列四个命题：①直径是弦；②经过三个点一定可以作圆；③三角形的外心到三角形各顶点的距离都相等；④半径相等的两个半圆是等弧．其中正确的有………………（　　）

（A）4个　 （B）3个　　（C）2个　　（D）1个

【提示】若三点在一条直线上，则不能作出过这三点的圆，故②不对．【答案】B．

【点评】本题考查直径、过不在同一条直线上的三点的圆、外心、等圆与等弧等概念，其中第②个命题不对的原因在于忽视了过三点作图的条件．

2．下列判断中正确的是………………………………………………………………（　　）

（A）平分弦的直线垂直于弦（B）平分弦的直线也必平分弦所对的两条弧

（C）弦的垂直平分线必平分弦所对的两条弧（D）平分一条弧的直线必平分这条弧所对的弦

【提示】弦的垂直平分线平分弦、垂直于弦，因此平分弦所对的两条弧．【答案】C．

3．如图，在两半径不同的同心圆中，∠AOB＝∠A′OB′＝60°，则………………（　　）

（A）＝（B）＞

（C）的度数＝的度数

（D）的长度＝的长度

【提示】因为在圆中，圆心角的度数与它所对的弧的度数相等，

而∠AOB＝∠A′OB′，所以的度数＝的度数．【答案】C．

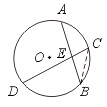
4．如图，已知⊙O的弦AB、CD相交于点E，的度数为60°，的度数为100°，则∠AEC等于………………………………………………………………………（　　）

（A）60°　　（B）100°　 （C）80°　 （D）130°

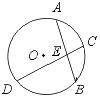
【提示】连结BC，则∠AEC＝∠B＋∠C＝×60°＋×100°＝80°．

【答案】C．

5．圆内接四边形ABCD中，∠A、∠B、∠C的度数比是2︰3︰6，则∠D的度数是（　  ）

（A）67.5°　　（B）135°　　（C）112.5°　　（D）110°

【提示】因为圆内接四边形的对角之和为180°，则∠A＋∠C＝∠B＋∠D＝180°．又因为∠A︰∠B︰∠C＝2︰3︰6，所以∠B︰∠D＝3︰5，所以∠D的度数为×180°＝112.5°．【答案】C．

6．OA平分∠BOC，P是OA上任一点，C不与点O重合，且以P为圆心的圆与OC相离，那么圆P与OB的位置关系是………………………………………………（　　）

（A）相离　 （B）相切　　（C）相交　　 （D）不确定

【提示】因为以点P为圆心的圆与OC相离，则P到OC的距离大于圆的半径．又因为角平分线上的一点到角的两边的距离相等，则点P到OB的距离也大于圆的半径，故圆P与OB也相离．【答案】A．

7．△ABC的三边长分别为a、b、c，它的内切圆的半径为r，则△ABC的面积为（　　）

（A）（a＋b＋c）r 　 （B）2（a＋b＋c）（C）（a＋b＋c）r　  （D）（a＋b＋c）r

【提示】连结内心与三个顶点，则△ABC的面积等于三个三角形的面积之和，所以△ABC的面积为a·r＋b·r＋c·r＝（a＋b＋c）r．【答案】A．

8．如图，已知四边形ABCD为圆内接四边形，AD为圆的直径，直线MN切圆于点B，DC的延长线交MN于G，且cos ∠ABM＝，则tan ∠BCG的值为……（　　）

（A）　　（B）　　（C）1　　（D）

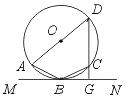
【提示】连结BD，则∠ABM＝∠ADB．因为AD为直径，所以∠A＋∠ADB＝90°，所以cos ∠ABM＝＝cos ∠ADB＝sin A，所以∠A＝60°．又因四边形ABCD内接于⊙O，所以∠BCG＝∠A＝60°．则tan ∠BCG＝． 【答案】D．　　　　　　　　 

9．在⊙O中，弦AB和CD相交于点P，若PA＝3，PB＝4，CD＝9，则以PC、PD

的长为根的一元二次方程为…………………………………………………………（　　）

（A）x²＋9 x＋12＝0　　（B）x²－9 x＋12＝0（C）x²＋7 x＋9＝0　　 （D）x²－7 x＋9＝0

【提示】设PC的长为a，则PD的长为（9－a），由相交弦定理得3×4＝a ·（9－a）．所以a²－9 a＋12＝0，故PC、PD的长是方程x²－9 x＋12＝0的两根．【答案】B．

10．已知半径分别为r和2 r的两圆相交，则这两圆的圆心距d的取值范围是………（　　）

（A）0＜d＜3 r　　　（B）r＜d＜3 r　　（C）r≤d＜3 r　　（D）r≤d≤3 r

【提示】当两圆相交时，圆心距d与两圆半径的关系为2 r－r＜d＜2 r＋r，即r＜d＜3 r．【答案】B．

（三）填空题（每题2分，共20分）

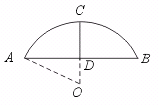
11．某公园的一石拱桥是圆弧形（劣弧），其跨度为24米，拱的半径为13米，则拱高为_____．

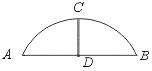
【提示】如图，AB为弦，CD为拱高，则CD⊥AB，AD＝BD，且O在CD的延长线上．连结OD、OA，则OD＝＝＝5（米）．所以

CD＝13－5＝8（米）． 【答案】8米．　　　　　　　　　　　　 

12．如图，已知AB为⊙O的直径，∠E＝20°，∠DBC＝50°，则∠CBE＝______．

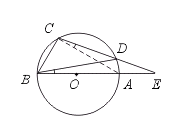
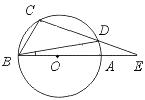
【提示】连结AC．设∠DCA＝x°，则∠DBA＝x°，所以∠CAB＝x°＋20°．因为AB为直径，所以∠BCA＝90°，则∠CBA＋∠CAB＝90°．

又　∠DBC＝50°，∴　50＋x＋（x＋20）＝90．

∴　x＝10．∴　∠CBE＝60°．【答案】60°．

13．圆内接梯形是_____梯形，圆内接平行四边形是_______．

【提示】因平行弦所夹的弧相等，等弧所对的弦相等，所以圆内接梯形是等腰梯形．同理可证圆内接平行四边形是矩形．【答案】等腰，矩形．

14．如图，AB、AC是⊙O的切线，将OB延长一倍至D，若∠DAC＝60°，则∠D＝_____．

【提示】连结OA．∵　AB、AC是⊙O的切线，∴　AO平分∠BAC，且OB⊥AB．又　OB＝BD，∴　OA＝DA．∴　∠OAB＝∠DAB．

∴　3∠DAB＝60°．∴　∠DAB＝20°．∴　∠D＝70°．

15．如图，BA与⊙O相切于B，OA与⊙O相交于E，若AB＝，EA＝1，则⊙O的半径为______．

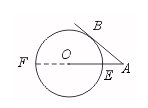
【提示】延长AO，交⊙O于点F．设⊙O的半径为r．　　　　　　　　　　　　　 

由切割线定理，得AB²＝AE·AF．∴ （）²＝1·（1＋2 r）．

∴　r＝2．【答案】2．

16．已知两圆的圆心距为3，半径分别为2和1，则这两圆有______条公切线．

【提示】因为圆心距等于两圆半径之和，所以这两圆外切，故有两条外公切线，一条内公切线．

【答案】3．

17．正八边形有_____条对称轴，它不仅是______对称图形，还是_____对称图形．

【提示】正n边形有n条对称轴．正2n边形既是轴对称图形，又是中心对称图形．

【答案】8，轴，中心．

18．边长为2 a的正六边形的面积为______．

【提示】把正六边形的中心与六个顶点连结起来，所得六个等边三角形全等．每个等边三角形的面积为·（2 a）²＝a²，所以正六边形的面积为6a²．

19．扇形的半径为6 cm，面积为9 cm²，那么扇形的弧长为______，扇形的圆心角度数为_____．

【提示】已知扇形面积为9 cm²，半径为6 cm，则弧长l＝＝3；设圆心角的度数为n，则＝3 cm，所以n＝．【答案】3；．

20．用一张面积为900 cm²的正方形硬纸片围成一个圆柱的侧面，则这个圆柱的底面直径

为_____．

【提示】面积为900 cm²的正方形的边长为30 cm，则底面圆的周长30 cm．设直径为d，则pd＝30，故d＝（cm）．【答案】 cm．

（三）判断题（每题2分，共10分）

21．相交两圆的公共弦垂直平分连结这两圆圆心的线段……………………………（　　）【答案】×．

【点评】相交两圆的连心线垂直平分公共弦，反过来公共弦不一定平分连结两圆圆心的线段．

22．各角都相等的圆内接多边形是正多边形…………………………………………（　　）【答案】×．

【点评】矩形内接于以对角线为直径的圆，但它不是正多边形．

23．正五边形既是轴对称图形，又是中心对称图形…………………………………（　　）【答案】×．

【点评】正五边形是轴对称图形，但不是中心对称图形．

24．三角形一定有内切圆………………………………………………………………（　　）【答案】√．

【点评】作三角形的两条角平分线，设交点为I，过I作一边的垂线段，则以点I为圆心，垂线段长为半径的圆即三角形的内切圆．

25．平分弦的直径垂直于弦……………………………………………………………（　　）【答案】×．

【点评】当被平分的弦为直径时，两直径不一定垂直．

（四）解答题：（共50分）

26．（8分）如图，⊙O的直径AB和弦CD相交于点E，且AE＝1 cm，EB＝5 cm，

∠DEB＝60°，求CD的长．

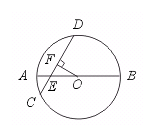
【分析】因为AE＝1 cm，EB＝5 cm，所以OE＝（1＋5）－1＝2（cm）．在Rt△OEF中可求EF的长，则EC、ED都可用DF表示，再用相交弦定理建立关于DF的方程，解方程求DF的长．

【略解】∵　AE＝1 cm，BE＝5 cm，∴　⊙O的半径为3 cm．∴　OE＝3－1＝2（cm）．在Rt△OEF中，∠OEF＝60°，∴　EF＝cos 60°·OE＝·2＝1（cm）．∵　OF⊥CD，∴　FC＝FD．∴　EC＝FC－FE＝FD－FE，ED＝EF＋FD．即　EC＝FD－1，ED＝FD＋1．由相交弦定理，得　AE·EB＝EC·ED．∴　1×5＝（FD－1）（FD＋1）．解此方程，得　FD＝（负值舍去）．∴　CD＝2FD＝2（cm）．

27．（8分）如图，AB为⊙O的直径，P为BA的延长线上一点，PC切⊙O于点C，

CD⊥AB，垂足为D，且PA＝4，PC＝8，求tan ∠ACD和sin ∠P的值．

【提示】连结CB，易证△PCA∽△PBC，所以＝．由切割线定理可求PB的长，所以

tan∠ACD＝tan ∠CBA＝＝．连结OC，则在Rt△OCP中可求

sin∠P的值．

【略解】连结OC、BC．∵　PC为⊙O的公切线，∴　PC²＝PA·PB．

∴　8²＝4·PB．∴　PB＝16．∴　AB＝16－4＝12．易证△PCA∽△PBC．∴　＝．∵　AB为⊙O的直径，∴　∠ACB＝90°．又　CD⊥AB，∴ ∠ACD＝∠B．∴ tan ∠ACD＝tan B＝＝＝＝．

∵　PC为⊙O的切线，∴　∠PCO＝90°．∴　sin P＝＝＝．

28．（8分）如图，已知ABCD是圆内接四边形，EB是⊙O的直径，且EB⊥AD，AD与BC的延长线交于F，求证＝．

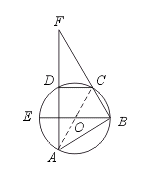【提示】连结AC，证△ABC∽△FDC．显然∠FDC＝∠ABC．因为AD⊥直径EB，由垂径定理得＝，故∠DAB＝∠ACB．又因为∠FCD＝∠DAB，所以

∠FCD＝∠ACB，故△ABC∽△FDC，则可得出待证的比例式．

【略证】连结AC．∵　AD⊥EB，且EB为直径，∴　＝．

∴　∠ACB＝∠DAB．∵　ABCD为圆内接四边形，∴　∠FCD＝∠DAB，∠FDC＝∠ABC．

∴　∠ACB＝∠FCD．∴　△ABC∽△FDC．∴　＝．

29．（12分）已知：如图，⊙O₁与⊙O₂内切于点P，过点P的直线交⊙O₁于点D，交⊙O₂于点E；DA与⊙O₂相切，切点为C．*（1）求证PC平分∠APD；（2）若PE＝3，PA＝6，求PC的长．

【提示】（1）过点P作两圆的公切线PT，利用弦切角进行角的转换；在（2）题中，可通过证△PCA∽△PEC，得到比例式＝，则可求PC．

*（1）【略证】过点P作两圆的公切线PT，连结CE．∵　∠TPC＝∠4，∠3＝∠D．

∴　∠4＝∠D＋∠5，∴　∠2＋∠3＝∠D＋∠5．∴　∠2＝∠5．

∵　DA与⊙O相切于点C，∴　∠5＝∠1．∴　∠1＝∠2．即PC平分∠APD．

（2）【解】∵　DA与⊙O₂相切于点C，∴　∠PCA＝∠4．

由（1），可知∠2＝∠1．∴　△PCA∽△PEC．

∴　＝．即　PC²＝PA·PE．∵　PE＝3，PA＝6，∴　PC²＝18．∴　PC＝3．

5．（14分）如图，⊙O是以AB为直径的△ABC的外接圆，点D是劣弧的中点，连

结AD并延长，与过C点的切线交于P，OD与BC相交于点E．（1）求证OE＝AC；

*（2）求证：＝；（3）当AC＝6，AB＝10时，求切线PC的长．

【提示】（1）因为AO＝BO，可证OE为△ABC的中位线，可通过证OE∥AC得到OE为中位线；（2）连结CD，则CD＝BD，可转化为证明＝．先证△PCD∽△PAC，得比例式＝，两边平方得＝，再结合切割线定理可证得＝＝；（3）利用（2）可求DP、AP，再利用勾股定理、切割线定理可求出PC的长．

（1）【略证】∵　AB为直径，∴ ∠ACB＝90°，

即　AC⊥BC．∵　D为的中点，由垂径定理，得

　OD⊥BC．∴　OD∥AC．又∵　点O为AB的中点，∴　点E为BC的中点．∴　OE＝AC．

*（2）【略证】连结CD．∵　∠PCD＝∠CAP，∠P是公共角，∴　△PCD∽△PAC．∴　＝．

∴　＝．又　PC是⊙O的切线，∴　PC²＝PD·DA．∴　＝，

∴　＝．∵　BD＝CD，∴　＝．

（3）【略解】在Rt△ABC中，AC＝6，AB＝10，∴　BC＝＝8．∴　BE＝4．

∵　OE＝＝3，∴　ED＝2．则在Rt△BED中，BD＝＝2，

在Rt△ADB中，AD＝＝4．∵　＝，∴　＝．

解此方程，得　PD＝5，AP＝9．又　PC²＝DP·AP，∴　PC＝＝15．