《整式的加减》基础测试

一　填空题（每小题3分，共18分）：

１．下列各式 －，3xy，a²－b²，，2x ＞1，－x，0.5＋x中，是整式的是　　　　　　　　　　　　　　　　　　　 ，是单项式的是　　　　　　　　　，是多项式的是　　　　　　　　　　　．

答案：、3xy、a²－b²、、－x、0.5＋x，

－、3xy、－x，

a²－b²、、0.5＋x．

评析：

　虽然有分数线，但是分母中不含有表示未知数的字母，所以它仍是整式；另一方面，有

　　　 ＝　 x－ y

所以我们认为它是多项式．在运用换元法时把它看作一个整体，也可以暂时看作单项式．

　　

2．a³b²c的系数是　　，次数是　　；　

答案：

１，６．

评析：

不能说a³b²c “没有系数”也不能说“它的系数是0”，实际上a³b²c ＝1a³b²c，系数“1”被省略了．单项式的次数是所有字母的指数和，在这里，字母c的指数“1” 被省略了，所以字母的指数和是“3＋2＋1 ＝ 6”，而不是“5”．　

　　　

３．3xy－5x⁴＋6x－1是关于x 的　　次　　项式；

答案：

４，４．

评析：

把组成多项式的各单项式中最高次项的次数作为这个多项式的次数．

４．－2x²y^m与xⁿy³是同类项，则 m ＝　　，n＝　　；

　答案：

　３，２．

评析：

根据同类项的意义“相同字母的指数也相同”可得．

 

5．3ab－5a²b²＋4a³－4按a降幂排列是　　　　　　　　　　　；

答案：

4a³－5a²b²＋3ab－4．

6．十位数字是m，个位数字比m小3，百位数字是m的3倍，这个三位数是　　　　　．

答案：

300m＋10m＋（m－3）或930．

评析：

百位数应表示为1003m ＝300m．一般地说，n位数

＝ a_n×10^n－1＋a_n－1×10^n－2＋a_n－2×10^n－3 ＋…＋a₃×10² ＋a₂×10＋a₁．

如　　 5273 ＝ 5×10³＋2×10²＋7×10＋3．

　　

因为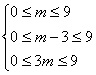　 解得m ＝3．

所以300m＋10m＋（m－3）＝930．

二　判断正误（每题3分，共12分）：

１．－3，－3x，－3x－3都是代数式…………………………………………………（　 ）

　答案：√．

评析：

－3，－3x都是单项式，－3x－3是多项式，它们都是整式，整式为代数式的一部分．

２．－7（a－b）²和 （a－b）² 可以看作同类项…………………………………（　 ）

答案：√．

评析：

把（a－b）看作一个整体，用一个字母（如m）表示，－7（a－b）²和 （a－b）²就可以化为 －7m²和m ²，它们就是同类项．

3．4a²－3的两个项是4a²，3…………………………………………………………（　 ）

答案：×．

评析：

多项式中的“项”，应是包含它前面的符号在内的单项式，所以4a²－3的第二项应是3， 而不是3．

4．x的系数与次数相同………………………………………………………………（　 ）

答案：√．

评析：

x的系数与次数都是1．

三　化简（每小题7分，共42分）：

1．a＋（a²－2a ）－（a －2a² ）；

　答案：3a²－2a．

评析：

注意去括号法则的应用，正确地合并同类项．

a＋（a²－2a）－（a－2a² ）

　＝a＋a²－2a－a＋2a²

　＝ 3a²－2a．

2．－3（2a＋3b）－（6a－12b）；

答案：－8a－5b．

评析：

注意，把 －3 和 －分别与二项式相乘的同时去掉括号，依乘法法则，括号内的各项都应变号．

　　　　　  －3 2a＋3b）－（6a－12b）

　　　　  ＝－6a－9b－2a＋4b

　　　　  ＝ －8a－5b．

３．－{－[－（－a ）²－b² ]}－[－（－b²）]；

答案：－a ²－2b²．

评析：注意多层符号的化简，要按次序逐步进行．

　　　　　　　　　 －{－[－（－a ）²－b² ]}－[－（－b²）]

　　　　　　　　  ＝－{－[ －a ²－b² ]}－b²

　　　　　　　　  ＝－{a ²＋b² }－b²

　　　　　　　　  ＝ －a ²－b² －b²

　　　　　　　　　　　　  ＝ －a ²－2b²

这里，－[－（－b² ）] ＝－b² 的化简是按照多重符号化简“奇数个负号结果为负”进行的；－[ －a ²－b² ] ＝ a ²＋b²，－{a ²＋b² }＝ －a ²－b²去括号法则进行的．要分析情况，灵活确定依据．

４．9x²－[7（x²－y）－（x²－y）－1]－；

答案：x² ＋3y－．

评析：注意区别情况，恰当引用法则，按次序逐步进行．

　　 9x²－[7（x²－y）－（x²－y）－1]－

　  ＝ 9x²－[7x² －2y－x²＋y－1]－　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　　 ＝9x²－7x² ＋2y＋x²－y＋1＋

　　 ＝ 3x² ＋y＋．

５．（3x^n＋2＋10xⁿ－7x）－（x－9x^n＋2 －10xⁿ）；

答案：12x^n＋2＋20xⁿ－8x．

评析：

注意字母指数的识别．

　　　　  （3x^n＋2＋10xⁿ－7x）－（x－9x^n＋2 －10xⁿ）

　　　　 ＝ 3x^n＋2＋10xⁿ－7x－x＋9x^n＋2＋10xⁿ

　　　　 ＝ 12x^n＋2＋20xⁿ－8x．

６．{ab－[ 3a²b－（4ab²＋ab）－4a²b]}＋3a²b．

答案：4a²b＋4ab² ＋ab．

评析：

注意多层括号的化简，要按次序由内而外逐步进行，并且注意随时合并同类项．

　　　　　　　　 {ab－[ 3a²b－（4ab²＋ab）－4a²b]}＋3a²b

　　　　　　　  ＝ {ab－[ 3a²b－4ab²－ab－4a²b]}＋3a²b

　　　　　　　  ＝ {ab－[ －a²b－4ab²－ab]}＋3a²b

　　　　　　　  ＝ab＋a²b＋4ab² ＋ab＋3a²b

　　　　　　　　 ＝ 4a²b＋4ab² ＋ab．

四　化简后求值（每小题11分，共22分）：

１．当a ＝－时，求代数式　

15a²－{－4a²＋[ 5a－8a²－（2a² －a ）＋9a² ]－3a }

的值．

答案：原式＝ 20a²－3a ＝．评析：先化简，再代入求值．

　　　　　　   15a²－{－4a²＋[ 5a－8a²－（2a² －a ）＋9a² ]－3a }

　　　　　　 ＝ 15a²－{－4a²＋[ 5a－8a²－2a²＋a＋9a² ]－3a }

　　　　  ＝ 15a²－{－4a²＋[ －a²＋6a ]－3a }

　　　　  ＝ 15a²－{－4a² －a²＋6a－3a }

　　　　  ＝ 15a²－{－5a²＋3a }

　　　　　　　　　　　 ＝ 15a²＋5a²－3a　

　　　　　　　　　  　 ＝ 20a²－3a，

　　　　　 把a ＝－　代入，得

原式＝ 20a²－3a ＝ 20 （－）²－3 （－）＝ 45＋＝ ．

２．已知a＋2＋（b＋1）² ＋（c－）² ＝ 0，求代数式

5abc－{2a²b－[3abc－（4ab² －a²b）]}的值．

答案：原式＝ 8abc －a²b－4ab²＝．

评析：

因为 a＋2＋（b＋1）² ＋（c－）² ＝ 0，

且 a＋2≥0，（b＋1）²≥0，（c－）²≥0，

所以有 ｜a＋2｜＝ 0，（b＋1）² ＝ 0，（c－）² ＝ 0，

于是有a ＝－2，b＝－1，c ＝ ．　

则有

　　　　　　　　　　　　　　 　5abc－{2a²b－[3abc－（4ab² －a²b）]}

　　　　　　　　　　　　　  ＝ 5abc－{2a²b－[3abc－4ab²＋a²b]}

　　　　　　　　　　　　　  ＝ 5abc－{2a²b－3abc＋4ab² －a²b}

　　　　　　　　　　　　　　＝ 5abc－{a²b－3abc＋4ab² }

　　　　　　　　　　　　　  ＝ 5abc －a²b＋3abc－4ab²

　　　　　　　　　　　　　  ＝ 8abc －a²b－4ab²

原式＝8×（－2）×（－1）×－（－2）²×（－1）－4×（－2）×（－1）²

＝＋４＋8

＝．