中考数学自测试题8
1.如图,把绕在横截面为正方形的线板上的细线(线的粗细忽略不计)逐渐展开,这时我们称线头A所经过的轨迹是一条渐开线.
渐开线与射线OM交于A,![]() ….若从A点到
….若从A点到![]() 点的渐开线为第1圈,从
点的渐开线为第1圈,从![]() 点到
点到![]() 点的回形线为第2圈,…,依此类推.
点的回形线为第2圈,…,依此类推.
若正方形横截面的边长为1,则渐开线第10圈的长为( B ).
(A) 76π (B) 77π (C) 78π (D) 79π
 | |||
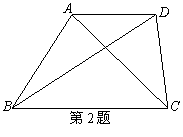 | |||
2.在梯形ABCD中,AD//BC,AD=1,BC=4,AC=3,
BD=4,则梯形ABCD的面积是 6
 3.在矩形ABCD中,
3.在矩形ABCD中,![]() ,
,![]() (
(![]() >
>![]() ),且
),且![]() 、
、![]() 是方程
是方程![]() 的两个根,P是BC上的一动点,动点Q在PC或其延长线上,BP=PQ,以PQ为一边的正方形为PQRS,点P从B点以
的两个根,P是BC上的一动点,动点Q在PC或其延长线上,BP=PQ,以PQ为一边的正方形为PQRS,点P从B点以![]() /秒的速度开始沿射线BC方向运动,设运动时间为
/秒的速度开始沿射线BC方向运动,设运动时间为![]() ,正方形PQRS与矩形ABCD重叠部分的面积为
,正方形PQRS与矩形ABCD重叠部分的面积为![]() ,
,
(1)求![]() 和
和![]() ;
;
(2)分别求出0≤![]() ≤2和2≤
≤2和2≤![]() ≤4时 ,
≤4时 ,![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)是否存在某一时刻,使重叠部分的面积是矩形ABCD面积的![]() ,若存在,请求出
,若存在,请求出![]() 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
答案:(1)![]() =4、
=4、![]() =2;(2)当0≤
=2;(2)当0≤![]() ≤2时,
≤2时,![]() ;当2≤
;当2≤![]() ≤4时 ,
≤4时 ,![]() =
=![]() ;
;
(3)当![]() 时,取
时,取![]() ;当
;当![]() =
=![]() =3时,
=3时,![]() ;
;
王江泾镇中学供稿
选择题:
已知抛物线![]() 与
与![]() 轴交于A、B两点,顶点为C,连结AC、BC,点A1、A2、A3、…
轴交于A、B两点,顶点为C,连结AC、BC,点A1、A2、A3、…![]() 把AC
把AC ![]() 等分,过各分点作
等分,过各分点作![]() 轴的平行线,分别交BC于B1、B2、B3、…
轴的平行线,分别交BC于B1、B2、B3、…![]() ,线段A1B1、A2B2、A3B3、…、
,线段A1B1、A2B2、A3B3、…、![]() 的和为( )。
的和为( )。
A.
2
B. ![]() C.
C.
![]() D.
D.
![]()
 填空题:
填空题:
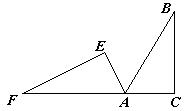
如图:斜边长为10的直角三角形△ABC中∠C=90°,有一个角∠B=30°,将直角三角形ABC绕着点A逆时针旋转成如图所示,使点F、A、C成一直线,再沿AC方向平移△AEF,使E点落在BC边上,则三角形AEF移动的距离为
 解答题:
解答题:
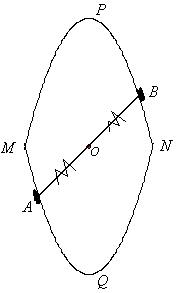
嘉兴历来被称为“鱼米之乡,丝绸之府”,特别是在建设社会主义新农村的今天,嘉兴的丝织业蓬勃发展,欣欣向荣,但同学们知道吗,在这里有我们的数学知识在默默地奉献。如图是高科技工业——喷气织机的一个自动装置。它有两部分组成:两条对称的抛物线型合成的活动底座和可以绕着底座中心O自由转动的有弹性的直轴AB。当直轴转动时,端点(A、B)也相应紧贴着底座运动。经测量,两抛物线的交接点M、N间的距离是10厘米,两顶点(P、Q)间的距离为50厘米.
(1) 若以O点为原点,直线MN为横轴作直角坐标系,求这两条抛物线的解析式,并写出相应的自变量取值范围;
(2) 当AB转动时(不与MN重合),求证:四边形AMBN始终是平行四边形;
(3) 当AB转动时(不与MN重合),平行四边形AMBN的面积有没有最大值和最小值,若存在,求出点A的坐标,并判断它是何种特殊平行四边形,求出它的面积;若不存在,请说明理由.
油车港镇中学初三备课组供稿
1.在△ABC中,AB=BC=9 ∠BAC=45º P是线段BC上任意一点(包括两端点B、C),若P关于AB、AC的对称点为E、F,则△AEF的最小面积是(
)(A) ![]() (B)
(B)![]() (C)
(C)![]() (D)不能确定
(D)不能确定
2.按照一定顺序排列的一列数叫数列,一般用a1 a2 a3 a4 ------ an 表示一个数列,可简记为{an},现有数列{an}满足如下关系式:an+1=an2-nan+1 (n=1,2,3------n) 且a1=2,根据已知条件计算a2 a3 a4 ------ an的值;若a1+ a2 + a3 + a4+
------+an=230 则n=____________
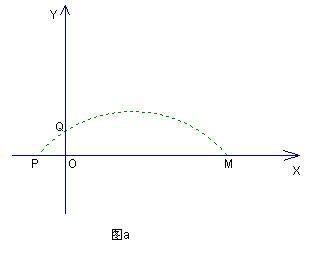
3.2006年世界杯在德国举行,最后意大利夺取了冠军。在足球比赛中,当守门员远离球门时,进攻队员常采用“挑射”战术(把球高高地挑过守门员的头顶,射向球门),现有一位球员在离对方球门若干米的M处起脚挑射,若球运行路线是一条抛物线,解析式为y=-![]() 如图a:以球门底部中心为坐标原点建立坐标系,球门OQ的高度为2.44米。
如图a:以球门底部中心为坐标原点建立坐标系,球门OQ的高度为2.44米。
① 球员起脚射门的地点M处距离球门多远?并通过计算说明,在无人阻挡的情况下,球是否会进球门?
② 如果守门员站在距离球门前1米处,他跳起后最多能摸到达2.75米高,问这次挑射他能否在空中截住?
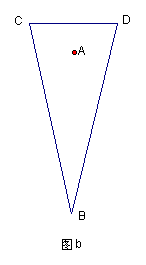
③ 如图b:在另一次地面进攻中,守门员站在球门中央的正前方,距离球门一定距离的点A处,现有一位进攻队员采用“地滚球”战术(球在地面上滚动,射向球门),他在离球门中央12米的B处起脚射门,球以平均![]() 米/秒的速度径直滚向立柱C,已知球门的宽度CD为7.2米。假如在球起脚的同时,守门员及时起动,平均速度为9米/秒。问:这次射门守门员能否挡住球?通过计算分析理由。
米/秒的速度径直滚向立柱C,已知球门的宽度CD为7.2米。假如在球起脚的同时,守门员及时起动,平均速度为9米/秒。问:这次射门守门员能否挡住球?通过计算分析理由。
参考答案:1. B 2. 20 3. ① 30米 ;会 过程略 ②不能,过程略
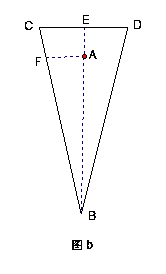
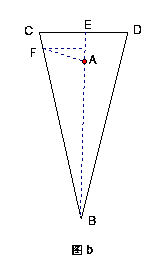
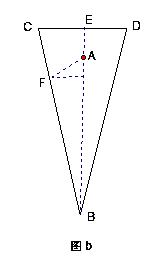 ③设时间为t秒,按下列三图进行分类讨论,可分析得出结论:无论哪种情形守门员都不能挡住球。
③设时间为t秒,按下列三图进行分类讨论,可分析得出结论:无论哪种情形守门员都不能挡住球。
新城中学供稿
1、选择题: 一般地,如果函数![]() 对于自变量取值范围的任意
对于自变量取值范围的任意![]() ,都有
,都有![]() ,那么
,那么![]() 就叫做奇函数, 例如:
就叫做奇函数, 例如: ![]() ,当
,当![]() 取任意实数时,
取任意实数时, ![]() , 即
, 即 ![]() , 因此
, 因此 ![]() 为奇函数。问在下列函数: ①
为奇函数。问在下列函数: ① ![]() , ②
, ② ![]() ③
③
![]() ④
④ ![]() ⑤
⑤
![]() 中,任意抽取2个函数,抽到全是奇函数的概率是( )
中,任意抽取2个函数,抽到全是奇函数的概率是( )
(A)1/5 (B)1/10 (C)1/15 (D)1/20
2、 填空题:四边形ABCD中,
填空题:四边形ABCD中,![]() ,AC平分
,AC平分![]() ,
,![]() ,
,![]() ,则 AB=
。
,则 AB=
。
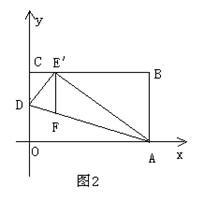
3、解答题:![]() 是一张放在平面直角坐标系中的矩形纸片,
是一张放在平面直角坐标系中的矩形纸片,![]() 为原点,点
为原点,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴上,
轴上,![]() ,
,![]()
(1)如图1,在![]() 上选取一点
上选取一点![]() ,将
,将![]() 沿
沿![]() 翻折,使点
翻折,使点![]() 落在
落在![]() 边上,记为
边上,记为![]() ,试求折痕
,试求折痕![]() 所在直线的解析式 .
所在直线的解析式 .
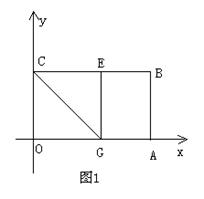
(2)如图2,在![]() 上选取一点
上选取一点![]() ,将
,将![]() 沿
沿![]() 翻折,使点
翻折,使点![]() 落在
落在![]() 边 上,记为E´.①求折痕
边 上,记为E´.①求折痕![]() 所在直线的解析式;②再作
所在直线的解析式;②再作![]() ∥
∥![]() ,交
,交![]() 于点
于点![]() .若抛物线
.若抛物线![]() 过点
过点![]() ,求此抛物线的解析式,并判断它与直线
,求此抛物线的解析式,并判断它与直线![]() 的交点的个数 .
的交点的个数 .
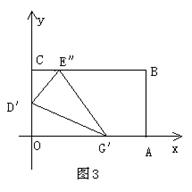
 (3)如图3,一般地,在
(3)如图3,一般地,在![]() 、
、![]() 上选取适当的点D´、G´,使纸片沿
上选取适当的点D´、G´,使纸片沿![]()
![]() 翻折后,点
翻折后,点![]() 落在
落在![]() 边上,记为E″.请你猜想:折痕
边上,记为E″.请你猜想:折痕![]()
![]() 所在直线与②中的抛物线会有什么关系?用①中的情形验证你的猜想.
所在直线与②中的抛物线会有什么关系?用①中的情形验证你的猜想.
![]()
参考答案:
1、 B 2、8
3、 解:(1)由折法知,四边形![]() 是正方形,∴
是正方形,∴![]() ,∴
,∴![]() ,
,![]() .
.
设直线![]() 的解析式为
的解析式为![]() ,则
,则![]() ,
,![]() .∴
.∴![]() ,
,![]() .
.
∴直线的解析式为:![]() .
.
(2) ①在![]() 中,
中,![]() ,∴
,∴![]() .设
.设![]() ,则
,则![]() ,
,![]() ,∴在
,∴在![]() 中,
中,![]() , ∴
, ∴![]() ,从而
,从而![]() .
.
设直线![]() 的解析式为:
的解析式为:![]() .由于它过
.由于它过![]() ,∴
,∴![]()
∴直线![]() 的解析式为
的解析式为![]() .
.
②∵![]() ∥
∥![]() ,
,![]() ,∴设
,∴设![]() .∵
.∵![]() 在
在![]() 上,∴
上,∴![]() ,
,
∴![]() .又
.又![]() 在抛物线上,∴
在抛物线上,∴![]() ,∴
,∴![]() .
.
∴抛物线的解析式为:![]() .
.
将![]() 代入
代入![]() ,得
,得![]() .
.
∵![]() ,∴直线
,∴直线![]() 与抛物线只有一个交点.
与抛物线只有一个交点.
(3)例如可作猜想:①折痕所在直线与抛物线![]() 只有一个交点;
只有一个交点;
或②若作![]() ∥
∥![]() ,交
,交![]() 于
于![]() .则
.则![]() 在抛物线
在抛物线![]() 上.
上.
验证:①在图1中,折痕为![]() .将
.将![]() 代入
代入![]() .
.
得![]() .∵
.∵![]() ,
,
∴折痕![]() 所在的直线的确与抛物线
所在的直线的确与抛物线![]() 只有一个交点.
只有一个交点.
②在图1中,![]() 即
即![]() ,
,![]() 即
即![]() ,
,![]() 即
即![]() ,交点
,交点![]() 也为
也为![]() .
.
∵当![]() 时,
时,![]() ,∴
,∴![]() 点在这条抛物线上.
点在这条抛物线上.
1、在如图(6)所示的三角形ABC中, AB=4,①中A1B1是连结两边中点的线段,易知A1B1=2,②中A1B1、A2B2是连结两腰三等分点且平行于底边的线段,可求出A1B1+A2B2的值……,照此规律下去,③中A1B1、A2B2,…A10B10是连结两边十一等分点且平行于底边的线段,则A1B1+A2B2+…+ A10B10的值为( B )
A.16 B.20 C.30 D.40

2、数字解密:第一个数是3=2+1,第二个数是5=3+2,第三个数是9=5+4,第四个数是17=9+8,……观察并猜想第六个数是 65 。
3、已知:f(x)=x2—2x,其中f(x)为函数,x为自变量,例如,f(1)=12—2×1= —1,
f(—2)=(—2)2—2×(—2)=8。则f(f(4))= 46
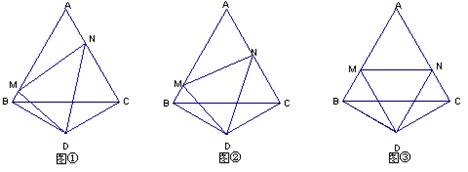
4、操作:如图①,△ABC是正三角形,△BDC是顶角∠BDC=120°的等腰三角形,以D为顶点作一个60°角,角的两边分别交AB、AC边于M、N两点,连接MN.
探究:线段BM、MN、NC之间的关系,并加以证明.![]()
说明:⑴如果你经历反复探索,没有找到解决问题的方法,请你把探索过程中的某种思路写出来(要求至少写3步);⑵在你经历说明⑴的过程之后,可以从下列①、②中选取一个补充或更换已知条件,完成你的证明.
注意:选取①完成证明得8分;选取②完成证明得5分.
①![]() (如图②); ②
(如图②); ②![]() (如图③).
(如图③).
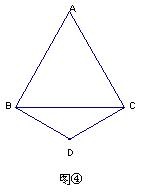
 附加题:若点M、N分别是射线AB、CA上的点,其它条件不变,再探线段BM、MN、NC之间的关系,在图④中画出图形,并说明理由.
附加题:若点M、N分别是射线AB、CA上的点,其它条件不变,再探线段BM、MN、NC之间的关系,在图④中画出图形,并说明理由.
4、解:BM+CN=MN ……………………………………1分
证明:如图,延长AC至M1,使CM1=BM,连结DM1 ……………………………2分
由已知条件知:∠ABC=∠ACB=60°,∠DBC=∠DCB=30°……………………3分
∴∠ABD=∠ACD=90° ……………………………………4分
∵BD=CD
∴Rt△BDM≌Rt△CDM1 ……………………………………5分
∴∠MDB=∠M1DC DM=DM1
∴∠MDM1=(120°-∠MDB)+∠M1DC=120°
又∵∠MDN=60°
∴∠M1DN=∠MDN=60°
∴△MDN≌△M1DN
∴MN=NM1=NC+CM1=NC+MB ……………………………………8分
附加题: CN-BM=MN
证明:如图,在CN上截取,使CM1=BM,连结DM1 ……………………………1分
∵∠ABC=∠ACB=60°,∠DBC=∠DCB=30°
∴∠DBM=∠DCM1=90°
∵BD=CD
∴Rt△BDM≌Rt△CDM1
∴∠MDB=∠M1DC DM=DM1 ……………………………2分
∵∠BDM+∠BDN=60°
∴∠CDM1+∠BDN=60°
∴∠NDM1=∠BDC-(∠M1DC+∠BDN)=120°-60°=60°
∴∠M1DN=∠MDN ……………………………………4分
∵AD=AD
∴△MDN≌△M1DN
∴MN=NM1=NC-CM1=NC-MB ……………………………………6分

