《分式》基础测试
一 填空题（每小题2分，共10分）：
1．已知v＝v0＋at(a不为零)，则t＝ ；
2．关于x的方程mx＝a (m
的解为 ；
3．方程 
的根是 ；
4．如果－3 是分式方程 
的增根，则a＝ ；
5．一汽车在a小时内走x千米，用同样的速度，b分钟可以走 千米．
答案：
１．
；２．
；３．
；４．3；５．
．
二 选择题（每小题3分，共12分）：
1．已知
＝2，用含x的代数式表示y，得……………………………………（ ）
（A）y＝2x＋8 （B）y＝2x＋10 （C）y＝2x－8 （D）y＝2x－10
2．下列关于x的方程，其中不是分式方程的是……………………………………（ ）
（A）
（B）
（C）
(D)
3．一件工程甲单独做a小时完成，乙单独做b小时完成，甲、乙二人合作完成此项工作需要的小时数是………………………………………………………………………（ ）
（A）a＋b （B）
（C）
（D）
4．解关于x的方程（m2－1）x＝m2－m－2 (m2≠1) 的解应表示为…………（ ）
（A）x＝
（B）x＝
（C）x＝
（D）以上答案都不对
答案：
１．Ｄ；２．Ｃ；３．Ｄ；４．Ｂ．
三 解下列方程（每小题8分，共32分）：
1．
； 2． 
；
解：
， 解：
，
，
，
，
，
，
，
，
，
．
．
经检验，
＝1是原方程的根．
经检验，＝2是原方程的增根．
3．
；
解：去分母，得
，
，
整理方程，得
，
，
．
经检验，＝2是原方程的根．
4．
．
解：整理方程，得
，
，
去分母，得
，
，
．
经检验， 是原方程的根．
四 解下列关于x的方程（1、2每小题7分，3小题8分，共22分）：
１．2ax－(3a－4)＝4x＋3a＋6；
解：整理，得
2ax－4x＝3a＋6＋3a－4，
(2a－4)x＝6a＋2，
(a－2)x＝3a＋1，
当a≠2时，方程的根为
，
当a＝2时，3a＋1≠0,
所以原方程无解；
2．m2 (x－n)＝n2 (x－m) (m2≠n2)；
解：整理，得
m2 x－m2 n＝n2 x－n2m，
移项，得
（m2－n2 )x＝m2 n－n2m，
因为m2≠n2 ，所以m2－n2≠0，则方程的根为
x＝
；
3．
．
解：去分母，得
，
，
，
因为
所以方程的根是
x＝
．
五 列方程解应用题（每小题8分，共２4分）
1．甲、乙两地相距135千米，大小两辆汽车从甲地开往乙地，大汽车比小汽车早出发5小时，小汽车比大汽辆早到30分钟，小汽车和大汽车的速度之比为5∶2，求两车的速度．
提示：设小汽车的速度为5x千米／时，大汽车的速度为2x千米／时．
根据题意，得:
，
解得x＝9，小汽车的速度为45千米／时，大汽车的速度为18千米／时．
2．一项工作A独做40天完成，B独做50天完成，先由A独做，再由B独做，共用46天完成，问A、B各做了几天？
提示：设甲做了x天，则乙做了（46－x）天．
据题意，得：
，
解得 x＝16，
甲做16天，乙做30天．
3．甲、乙两种食品都含糖，它们的含糖量之比为2∶3，其他原料含量之比为1∶2，重量之比为40∶77，求甲、乙两种食品含糖量的百分比分别是多少．
提示：设甲种食品含糖量为2x克，其他原料y克；
则乙种食品含糖量为3x克，其他原料2y克．
据题意，得：
，
解得 y＝
，
则甲、乙两种食品含糖量的百分比分别为
甲种： 
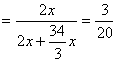＝15%；
乙种： 15%
%．