《函数》基础测试

（一）选择题（每题4分，共32分）

1．下列各点中，在第一象限内的点是………………………………………………（　　）

（A）（－5，－3）　 （B）（－5，3）　 （C）（5，－3）　 （D）（5，3）

【提示】第一象限内的点，横坐标、纵坐标均为正数．【答案】D．

2．点P（－3，4）关于原点对称的点的坐标是……………………………………（　　）

（A）（3，4）　 （B）（－3，－4）　 （C）（－4，3）　 （D）（3，－4）

【提示】关于原点对称的两个点的横、纵坐标分别互为相反数．【答案】D．

3．若点P（a，b）在第四象限，则点Q（－a，b－4）在象限是………………（　　）

（A）第一象限　　（B）第二象限　　（C）第三象限　　（D）第四象限

【提示】由题意得a＞0，b＜0，故－a＜0，b－4＜0．【答案】C．

4．函数y＝＋中自变量x的取值范围是……………………………（　　）

（A）x≤2　  （B）x＝3　　（C）x＜2且x≠3　　（D）x≤2且x≠3

【提示】由2－x≥0且x－3≠0，得x≤2．

【答案】A．

【点评】注意：D的错误是因为x≤2时x已不可能为3．

5．设y＝y₁＋y₂，且y₁与x²成正比例，y₂与成反比例，则y与x的函数关系是（　  ）

（A）正比例函数　　（B）一次函数　　（C）二次函数　　（D）反比例函数

【提示】设y₁＝k₁x²（k₁≠0），y₂＝＝k₂x（k₂≠0），则y＝k₁x²＋k₂x（k₁≠0，k₂≠0）．

【答案】C．

6．若点（－m，n）在反比例函数y＝的图象上，那么下列各点中一定也在此图象上的点是……………………………………………………………………………………（　　）

（A）（m，n）　 （B）（－m，－n）　 （C）（m，－n）　 （D）（－n，－m）

【提示】由已知得k＝－mn，故C中坐标合题意．

【答案】C．

7．二次函数式y＝x²－2 x＋3配方后，结果正确的是………………………………（　　）

（A）y＝（x＋1）²－2　　　 （B）y＝（x－1）²＋2

（C）y＝（x＋2）²＋3　　　 （D）y＝（x－1）²＋4

【提示】y＝x²－2 x＋3＝x²－2 x＋1＋2＝（x－1）²＋2．

【答案】B．

8．若二次函数y＝2 x²－2 mx＋2 m²－2的图象的顶点在x 轴上，则m 的值是（　  ）

（A）0　　（B）±1　　 （C）±2　　　（D）±

【提示】由题意知D ＝0，即4 m²－8 m²＋8＝0，故m＝±．

【答案】D．

【点评】抛物线的顶点在x 轴上，表明抛物线与x 轴只有一个交点，此时 D ＝0．

（二）填空题（每小题4分，共28分）

9．函数y＝中自变量x 的取值范围是___________．

【提示】由题意，得x－1≠0，x－3≠0．

【答案】x≠1，且x≠3．

【点评】注意零指数的底数不为0以及结论中的“且”字．

10．若反比例函数的图象过点（－1，2），则它的解析式为__________．

【提示】设反比例函数解析式为y＝，则k＝－2．

【答案】y＝－．

11．当m＝_________时，函数（m²－m）是一次函数．

【提示】2 m²－m＝1，解得m₁＝－，m₂＝1（舍去）．

【答案】m＝－．

【点评】根据一次函数的定义，得2 m²－m＝1，且m²－m≠0．

12．已知一次函数y＝kx＋b（k≠0），当x＝1时，y＝3；当x＝0时，y＝2．则函数解析式为________，函数不经过第_____象限，y 随x 增大而________．

【提示】设一次函数为y＝kx＋b，把已知值代入求出k，b．

【答案】y＝x＋2，四，增大．

【点评】本题考查一次函数的性质与解析式的求法．

13．二次函数y＝－x²＋mx＋2的最大值是，则常数m＝_________．

【提示】可应用顶点坐标公式求出顶点纵坐标．

【答案】±1．

【点评】本题考查二次函数最大（小）值的求法．本题还可用配方法求解．

14．如果二次函数y＝ax²＋bx＋c 的图象的顶点是（－2，4），且过点（－3，0），则a为_____________．

【提示】用顶点式求出二次函数解析式．

【答案】－4．

15．若直线y＝3 x＋b 与两坐标轴所围成的三角形的面积为24，则b＝_________．

【提示】直线与y 轴交点坐标为（0，b），与x 轴交点坐标为（－，0），故

24＝·b·－．

【答案】±12．

【点评】根据直线与x 轴、y 轴交点坐标的求法．求面积时对含b 的式子要加绝对值符号．

（三）解答题

16．（6分）已知正比例函数的图象经过点（1，－2），求此函数的解析式，并在坐标系中画出此函数的图象．

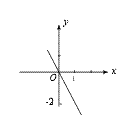【解】设正比例函数解析式为y＝kx（k≠0）．

∵　图象过（1，－2），

∴ －2＝k．

∴　函数解析式为y＝－2 x．

其图象如右图所示．

17．（8分）按下列条件，求二次函数的解析式：

（1）图象经过A（0，1），B（1，3），C（－1，1）；

（2）图象经过（3，1），且当x＝2时有最大值为3．

【答案】（1）y＝x²＋x＋1；（2）y＝－2 x²＋8 x－5．

【点评】要会用待定系数法求抛物线的解析式，（2）中隐含顶点坐标为（2，3）．

18．（8分）已知二次函数y＝2 x²－4 x－6．

（1）求图象的开口方向、对称轴、顶点坐标，并画出草图．

（2）求图象与x 轴的交点坐标，与y 轴的交点坐标．

（3）当x 为何值时，y 随x 的增大而增大？

（4）x 为何值时y≥0？

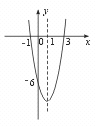
【解】（1）图象开口向上，对称轴为x＝1，顶点坐标为（1，－8）；

（2）与x 轴交于（－1，0），（3，0）两点，与y 轴交于（0，－6）；

（3）当x＞1时，y 随x 增大而增大；

（4）当x≤－1或x≥3时，y≥0．

19．（8分）某商场销售一批衬衫，平均每天可售出20件，每件盈利40元，为扩大销售增加盈利，尽快减少库存，商场决定采取降价措施，经调查发现，若每件衬衫每降价1元，商场平均每天可以多售出2件．（1）若每件降价x 元，每天盈利y 元，求y 与x 的关系式．（2）若商场平均每天要盈利1200元，每件衬衫应降价多少元？（3）每件衬衫降价多少元时，商场每天盈利最多？盈利多少元？

【解】（1）y＝（40－x ）（2 x＋20）＝－2 x²＋60 x＋800．

（2）当y＝1200时，

－2 x²＋60 x＋800＝1200，

∴　　　　　　　　　　  x₁＝10，x₂＝20．

∵　要尽快减小库存，

∴　x＝20．

（3）y＝－2（x－15）²＋1250，故每件降价15元时，最多盈利可达1250元．

【点评】要注意尽量减少库存的隐含条件．

20．（10分）已知x 轴上有两点A（x₁，0），B（x₂，0），在y 轴上有一点C，x₁，x₂ 是方程x²－m²x－5＝0的两个根，且＝26，△ABC 的面积是9．（1）求A，B，C 三点的坐标；（2）求过A，B，C 三点的抛物线的解析式．

【解】（1）∵　x₁＋x₂＝m²，x₁x₂＝－5，

∴　＝（x₁＋x₂ ）²－2 x₁x₂＝m⁴＋10＝26．

∴　m²＝4，则方程为x²－4 x－5＝0．

故x₁＝5，x₂＝－1．

∴　A（－1，0），B（5，0）或A（5，0），B（－1，0）．

设C点坐标为（0，c）．

∵　AB＝＝6，S_△ABC＝AB·h＝9，

∴　h＝±3．

∴　C（0，3）或（0，－3）．

（2）抛物线的解析式为

y＝－＋x＋3或y＝－x－3．