中考数学模拟4

姓名___________得分_________

一、选择题：（共40分）

题号	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
答案

1．已知－5的相反数是a，则a是　　　　 

A．5；　B．；　C．； D．－5．

2．下列三个事件：① 今年夏天，泸州会下冰雹；　② 将花生油滴入水中，花生油会浮在水面上； ③ 任意投掷一枚质地均匀的硬币，硬币停止后，正面朝上；

是必然事件的是　　　 A．①②； B．①③； C． ②③ ；D．②

3．用科学记数法表示0.00032，正确的是　　　　　　　　　　　　　　　　　　 

A． 　 B．　 C．　 D．

4．下列各式由左边到右边的变形中，是分解因式的为：

A ．　 B．

　　　 C．　　D．

5．如图1所示，圆柱的俯视图是

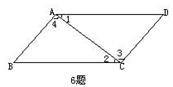
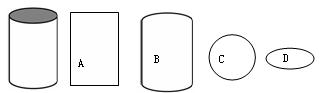
图1

6．如图，∠1=∠2，则下列结论一定成立的是

A．AB∥CD　　　　B．AD∥BC　　　 C．∠B=∠D　　D．∠3=∠4

7．据江阳气象台“天气预报”报道，今天的最低气温是17℃，最高气温是25℃，则今天气温t（℃）的范围是　 A．t＜17　B．t＞25　 C．t=21　　 D．17≤t≤25

8．两圆的半径分别为3㎝和4㎝，圆心距为1㎝，则两圆的位置关系是

A．外切　　　　B．内切　　　　C．相交　　　　 D．外离

9．某校计划修建一座既是中心对称图形又是轴对称图形的花坛，从学生中征集到的设计方案有正三角形、正五边形、等腰梯形、菱形等四种图案，你认为符合条件的是　

A．正三角形　　  B．正五边形　　 C．等腰梯形　　　　D．菱形

10．在一张比例尺是1∶500的地图上，一个图形的实际面积是625m²，则在地图上的面积为　　A．25m²　　　 B．25cm²  C．1.25m² 　 D．125m²

11．用一批完全相同的正多边形木板铺地面，要求顶点聚在一起，且木板之间没有缝隙，下列木板不符合要求的

A.正三角形木板　B.正方形木板　C.正五边形木板　 D. 正六边形木板

12．如图，梯形ABCD内接于⊙O，AB//CD，AB为直径，DO平分∠ADC，则∠DAO的度数是　　 A．90⁰； B．80⁰；　C．70⁰；　D．60⁰．

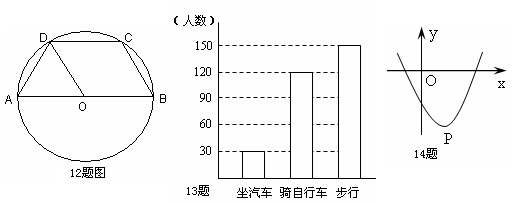13．如图是某校初一年学生到校方式的条形统计图，根据图形可得出步行人数占总人数的

A．60%；　　　　　　 B．50%；　　　　C．30%；　　　　　　 D．20%.

14．如图，抛物线的顶点P的坐标是（1，－3），则此抛物线对应的二次函数有

A．最大值1　　　B．最小值－3　　C．最大值－3　　　D．最小值1

15．一个箱子中放有红、黄、黑三种小球，三个人先后去摸球，一人摸一次，一次摸出一个小球，摸出后放回，摸出黑色小球为赢，这个游戏是

A．公平的；　B．不公平的； C．先摸者赢的可能性大； D．后摸者赢的可能性大.

二、每题6分，共18分

16．（1）计算：　　　　  （2）解方程：

（3）以如图所示的方格纸中，每个小正方形的边长为1，如果以MN所在的直线为y轴，以小正方形的边长为单位长度建立平面直角坐标系，使A点与B点关于原点对称，①在图中画出x轴与y轴；②这时C点的坐标是_________.

三、每题7分，共21分

17．已知，求·的值

18．已知：如图，四边形ABCD是菱形，E是BD延长线上一点，F是DB延长线上一点，且DE=BF．请你以F为一个端点，和图中已标明字母的某一点连成一条新的线段，猜想并证明它和图中已有的某一条线段相等（只须证明一组线段相等即可）．

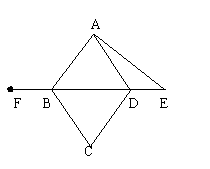　　（1）连结____________；

　　（2）猜想：______=______；

　　（3）证明：

19．某校学生会在“暑假社会实践”活动中组织学生进行社会调查，并组织评委会对学生写出的调查报告进行了评比．学生会随机抽取了部分评比后的调查报告进行统计，绘制了统计图如下，请根据该图回答下列问题：
(l)学生会共抽取了______份调查报告；
(2)若等第A为优秀，则优秀率为_____________ ；
(3)学生会共收到调查报告1000 份，请估计该校有多少份调查报告的等第为E ?

四、每题8分，共16分

20．一个弹簧不挂物体时长10㎝，挂上物体后会伸长（所挂物体不能超过20kg），在弹性限度内，弹簧伸长的长度与所挂的质量成正比例；如果挂上5㎏物体后，弹簧总长是㎝。

（1）求弹簧总长与所挂物体质量之间的函数关系式。

（2）求自变量x的取值范围，并在右下角的直角坐标系中画出此函数的图象。

21． 如图，AB切⊙O于点B，OA交⊙O于C点，过C作DC⊥OA交AB于D，

且BD︰AD=1︰2

（1）求∠A的正切值;

（2）若OC =1，求切线长AB及弧BC的长.

2007中考数学模拟4－B卷

姓名____________得分_______

一、填空（15分）

1．用一个平面去截一个正方体其截面形状不可能的是　　　　　　　　　  （请你在三角形、四边形、五边形、六边形、七边形这五种图形中选择符合题意的图形填上即可）；

2．已知m是方程的一个根，则代数式的值等于　　　.

3．有一个多项式为a⁸－a⁷b＋a⁶b²－a⁵b³＋…，按照此规律写下去，这个多项式的第八项是　　　 .

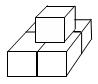
4．如图，5个边长为1cm的立方体摆在桌子上，则露在表面的部分的面积为__________.

5．溶液的酸碱度由pH确定．当pH＞7时，溶液呈碱性；当pH＜7时，溶液呈酸性．若将给定的HCl溶液加水稀释，那么在下列图象中，能反映HCl溶液的pH与所加水的体积（V）的变化关系的是________(填番号)

　　　①　　　　　　  ②　　　　　　　　  ③　　　　　　　　　 ④　　 

二、（每题7分，共14分）

6．光明中学9年级甲、乙两班在为“希望工程”捐款活动中，两班捐款的总数相同，均多于300元且少于400元．已知甲班有一人捐6元，其余每人都捐9元；乙班有一人捐13元，其余每人都捐8元．求甲、乙两班学生总人数共是多少人？

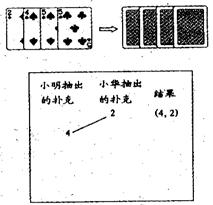7．如图，小明，小华用四张扑克牌玩游戏，他俩将扑克牌洗均匀后，背面朝上放置在桌面上，小明先抽，小华后抽，抽出的牌不放回．

（1）若小明恰好抽到的黑桃4．

 ①请在右边筐中绘制这种情况的树状图；

 ②求小华抽出的牌的牌面数字比4大的概率．

（2）小明、小华约定：若小明抽到的牌的牌面数字比小华的大，则小明胜；反之，则小明负，你认为这个游戏是否公平？若公平请说明你的理由．若不公平，请修改他们的约定使游戏公平。

三、（8题9分，9题12分，共21分）

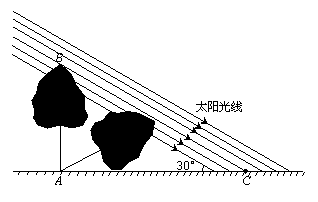
8．某数学兴趣小组，利用树影测量树高．已测出树AB的影长AC为9米，并测出此时太阳光线与地面成30°夹角．

（1）求出树高AB；

（2）因水土流失，此时树AB沿太阳光线方向倒下，在倾倒过程中，树影长度发生了变化，假设太阳光线与地面夹角保持不变，试求树影的最大长度．

（计算结果精确到0.1米，参考数据：≈1.414， ≈1.732）

 

 

 

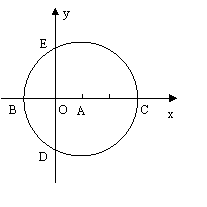
9．如图，在直角坐标系中，以点A(，0)为圆心，以为半径的圆与x轴相交于点B，C，与y轴相交于点D，E。

(1) 若抛物线经过C，D两点，求抛物线的解析式，并判断点B是否在该抛物线上。

(2) 在(1)中的抛物线的对称轴上求一点P，使得ΔPBD的周长最小。

(3) 设Q为(1)中的抛物线的对称轴上的一点，在抛物线上是否存在这样的点M，使得四边形BCQM是平行四边形。若存在，求出点M的坐标；若不存在，说明理由。