中考数学模拟测试题1

(考试时间：120分钟　满分：120分)

一、选择题（每题3分，共36分）

1. 下列运算中，正确的是（　 ）

A. 2x⁵－3x³=－x²　　　　　  B.

C. (－x)⁵·(－x²)= －x¹⁰　　　D. (3a⁶x³－9ax⁵)÷(－3ax³)=3x²－a⁵

2. 据2006年5月27日《沈阳日报》报道，“五·一”黄金周期间2006年沈阳“世园会”的旅游接待量累计人次，用科学记数法表示为(　 )

A. 176×10⁴人次　　　　　　 B. 17.6×10⁵人次　

C. 1.76×10⁶人次　　　　　　 D. 0.176×10⁷人次

3. 某中学人数相等的甲、乙两班的学生参加了同一次数学测验，各班平均分和方差分别为=82分，=82分，=245，=190，那么成绩较为整齐的是（　　 ）

A. 甲班　　　　　　 B. 乙班　　

C. 两班一样整齐　　 D. 无法确定

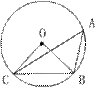
4. 如图，A、B、C是⊙O上的三点，⊙O的

半径为2cm，∠BAC=45⁰，则弦BC的长是（　　）　

A. 2cm　　　 B. 　　 C. 3cm　　　D.

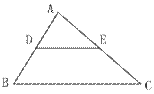
5. 如图，DE是△ABC的中位线，△ADE的

面积为3cm²，则梯形DBCE的面积为（　　 ）

A. 6cm²　　　　　B. 9cm²　　　 

C. 12cm²　 　　　D. 24cm²

6. 在△ABC中，∠C=90⁰， BC=2，sinA=，则边AC的长是（　　）

A．　　  B．3　　　C．　　  D．

7. 由几个小立方体搭成的一个几何体如图1所示，

它的主视图见图2，那么它的俯视图为（　　）

A.　　　　　  B.　　　　　　  C.　　　　　  D.

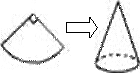8. 如图，现有一圆心角为90⁰，半径为8cm的扇形纸片，用它恰好围成一个圆锥的侧面（接缝忽略不计），则该圆锥底面圆的

半径为（　　　）

A. 4cm　　 B. 3cm　　C. 2cm　　 D. 1cm

9. 如图所示，边长分别为1和2的两个正方形，其一边在同一水平线上，小正方形沿该水平线自左向右匀速穿过大正方形，设穿过的时间为t，大正方形内除去小正方形部分的面积为S，

　　　

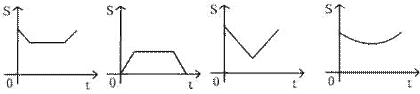　　　　　 A　　　　　  B　　　　　 C　　　　　　 D

10． 在元旦晚会上有一个闯关活动；将5张分别画有等腰梯形、圆、平行四边形、等腰三角形、菱形的卡片任意摆放，将有图形的一面朝下，从中任意翻开一张，如果翻开的图形是轴对称图形，就可以过关，那么一次过关的概率是（　　　）

A. 0.2　　　　  B. 0.4　　　　 C. 0.6　　　　　 D. 0.8

11. 小刚学习了有理数运算后，编了一个计算程序，当他输入任意一个有理数时，显示屏上出现的结果总等于所输入的数的平方与1的和，他第一次输入－2，然后又将所得的结果再次输入后，显示屏上出现的结果应是（　　 ）

A. －8　　　　  B. 5　　　　  C. －24　　　　 D. 26

12. 如图，小正方形边长为1，连接小正方形的三个顶点，可得△ABC，则AC边上的高是（　　　）

A. 　　　　　 B. 　　

C. 　　　　　 D.

二、填空题（每题3分，共18分）

13. 分解因式：a⁴－1= 　　　　　　

14. 一次函数的图象经过点（－1，0），且函数值随着自变量的增大而减小，写出一个符合这个条件的一次函数解析式：　　　　　　　　

15. 某校九年级毕业时，每一个同学都将自己的相片向全班其他同学各送了一张留念。全班共送了2250张相片，如果全班有x名学生，根据题意列出方程应为 　　　　　　　　　　（只列方程，不解答）

16. 已知m，n是方程x²－2004x+2005=0的两根，则（m²－2004m）与（n²－2004n+2006）的积是　　　　　 

17．计算： 　　　　 

18. 如图，矩形ABCD与圆心在AB上的⊙O交于点G、B、F、E，GB=8cm。DE=2cm，则EF=　　　　  cm

三、解答题（合计66分）

19. 解答下列各题（每小题6分，共12分）

（1）先化简，在求值：

，其中x=3－

（2）解方程：

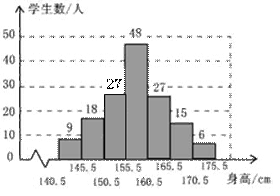
20. （满分10分）要了解某地区八年级学生的身高情况，从中随机抽取150名学生的身高作为一个样本，身高均在141cm～175cm之间（取整数厘米），整理后分成7组，绘制出频数分布直方图（不完整）。根据图中提供的信息，解答下列问题：

（1）补全频数分布直方图；

（2）抽取的样本中，学生身高的中位数在哪个小组？

（3）该地区共有3000名八年级学生，估计其中身高不低于161cm的人数。

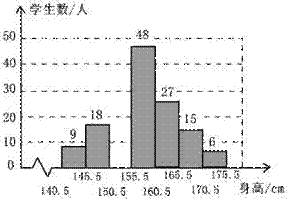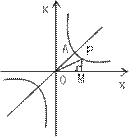21、（满分6分）比例函数y=（k>0）的图象上的任意一点，过P做

x轴的垂线，垂足为M，已知=2。

（1）求k的值；

（2）若直线y=x与反比例函数的图象在

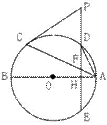第一象限交于点A，求过点A和点B（0，－2）的

直线的解析式。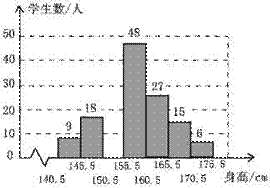

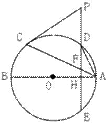
22（满分8分） 如图，AB，AC分别是⊙O的

直径和弦，点D为劣弧AC(⌒)上一点，弦ED分别交⊙O

于点E，交AB于点H，交AC于点F，过点C的切线

交ED的延长线于点P。

（1）若PC=PF，求证：AB⊥ED

（2）点D在劣弧AC(⌒)的什么位置时，才能使AD²=DE·DF，为什么？

23、（满分10分）某公司经营甲、乙两种商品，每件甲种商品进价12万元，售价14.5万元；每件乙种商品进价8万元，售价10万元，且它们的进价和售价始终不变，现准备购进甲、乙两种商品共20件，所用资金不低于190万元，不高于200万元。

（1）该公司有哪几种进货方案？

（2）该公司采取哪种进货方案可获得最大利润？做大利润是多少？

（3）若用（2）中所求得的利润再次进货，请直接写出获得最大利润的进

货方案。

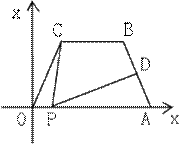
24、（满分10分）如图所示，在平面直角坐标系中，四边形OABC是等腰梯形，BC∥OA，OA=7，AB=4，∠COA=60⁰，点P为x轴上的一个动点，点P不与点O、点A重合，连结CP，过点P做PD交AB于点D。

（1）求点B的坐标；

（2）当点P运动什么位置时，△OCP为等腰三角形，求这时点P的坐标；

（3）当点P运动什么位置时，使得∠CPD=∠OAB，且BD：AB=5：8，求这时点P的坐标。

参考答案

一、选择题

1. D　 2. C　 3. B　　 4. D　　 5. B　　6. A　

7. C　 8. C　 9. A　　10. D　　11. D　 12. A

二、填空题

13. (a²+1)(a+1)(a－1)　　　 14. 写出一个符合要求的即

15. 　　 16. －2005　　17. 1　　 18. 6　　

三、解答题

19. （1）－　　　　　 （2）x=－ （分式方程一定要检验）　

20. （1）补全频数分布直方图如图所示：

（2）抽取的样本中，学生身高的中位数在155.5cm～160.5cm小组内。

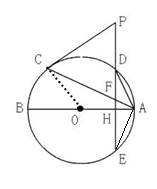（3）该地区身高不低于161cm的八年级学生人数估计有960人。

21. （1）k=4　（2）y=2x－2

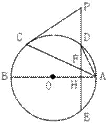
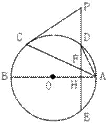
22. 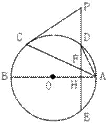（1）连接OC，∵PC=PF ∴∠PCF=∠PFC

∵∠PFC=∠AFH ∴∠AFH=∠PCF ∵OA=OC

∴∠OCA=∠OAC ∵PC切⊙O于点C，∴OC⊥PC

∴∠OCA+∠PCF=90⁰ ∴∠OCA+∠AFH=90⁰

∴∠AHF=90⁰，即AB⊥DE

（2）D在劣弧AC(⌒)的中点时，才能使AD²=DE·DF。

连结AE，可以证明△ADF∽△EDA。

23、（1）设购进甲种商品x件，乙种商品（20－x）件。

190≤12x+8(20－x)≤200，

解得7.5≤x≤10 ∵x为非负整数 ∴x取8，9，10

有三种进货方案：

购甲种商品8件，乙种商品12件。

购甲种商品9件，乙种商品11件。

购甲种商品10件，乙种商品10件。

（2）购甲种商品10件，乙种商品10件。可获得最大利润。最大利润是45万元。

（3）购甲种商品1件，乙种商品4件时，可获得最大利润。

23、（1）过B点作BE⊥OA，垂足是E。B点的坐标（5，）。　

（2）P点的坐标为(4,0)或（－4，0）。

　 （3）P点的坐标为（1，0）；（6，0）。

□山东省微山县欢城镇第二中学　　 郝　平

（电话：　　邮编：277606）