中考数学模拟卷(一)
（说明：本卷满分为120分，考试时间为120分钟）
一、填空题 （本大题共10小题，每小题3分，共30分）
1.－1－2＝ .
2.a（a－1）－a2＝ .
3.两圆半径分别为2、3，两圆圆心距为d，则两圆相交时d的取值范围为 ．
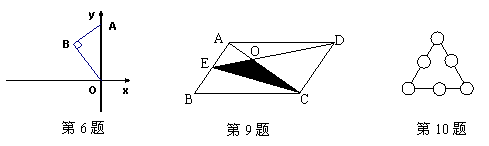
4.若反比例函数
与一次函数
的图象都经过点A（a，2），则m= .
| 命中环数 | 5 | 6 | 7 | 8 | 9 | 10 |
| 甲命中环数的次数 | 1 | 4 | 2 | 1 | 1 | 1 |
| 乙命中环数的次数 | 1 | 2 | 4 | 2 | 1 | 0 |
5.甲、乙两名学生进行射击练习，两人在相同条件下各射靶10次,将射击结果作统计分析如下:
从射击稳定性方面评价甲、乙两人的射击水平，则 比较稳定.
6.如图，Rt△AOB的斜边OA在y轴上，且OA=5，OB=4，将Rt△AOB绕原点O逆时针旋转一定的角度，使直角边OB落在x轴的负半轴上，得相应的△A’OB’，则A’点的坐标是 ．
7.在课题学习时，老师布置画一个三角形ABC，使∠A=30°，AB=10cm, ∠A的对边可以在长为4cm、5cm、6cm、11cm四条线段中任选，这样的三角形可以画 个．
8.同时向空中掷两枚质地完全相同的硬币，则出现同时正面朝上的概率为 .
9.如图，平行四边形ABCD的面积为24，E为AB上的中点，连接CE、AC，DE、AC的交点为O，则三角形OCE的面积为 .
10.如图，在一个由6个圆圈组成的三角形里，把1到6这6个数分别填入图的圆圈中，要求三角形的每条边上的三个数的和（S）都相等，那么S的最大值是 .
 |
二、选择题（本大题共6小题，每小题3分，共18分）
每小题有四个选项，其中只有一个选项是正确的，将正确选项的字母填入下表相应的题号下面
| 题号 | 11 | 12 | 13 | 14 | 15 | 16 |
| 答案 |
11.下图中几何体的左视图不可能是 （ ）
 |
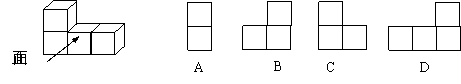12.小颖家买了一套新房正在进行装修，星期天小斌陪父母一起到瓷砖商店去购买一种多边形形状的瓷砖，用来铺设客厅地面（需无缝），则购买的瓷砖形状不可以是
A.三角形地砖 B.正方形地砖 C. 正六边形地砖 D. 正五边形地砖
13.家在农村的小李家卖猪，为了揭露收购者短斤少两的行为，在收购者称一头猪重207斤并还没有被放下的时候，快速在猪身上放了事先称好的准确的10斤重的铁块，结果称得216斤.假设猪的实际重x斤，则根据题意，列方程得（ ）
A．
Ｂ．
Ｃ．
Ｄ．
14.劳技课上，王芳制作了一个圆锥形纸帽，其尺寸如图．则将这个纸帽展开成扇形时的圆心角等于（ ）
A．45° Ｂ．60° C．90° Ｄ．120°
15.如图1，CD是Rt△ABC斜边AB上的高，将△BCD沿CD折叠，B点恰好落在AB的中点E处，则∠A等于 （ ）
A．25° B．30° C．45° D．60°
16.在直角坐标系中，0为坐标原点，A(1，1)，在x轴上确定一点P，使△AOP为等腰三角形，则符合条件的点P共有( )
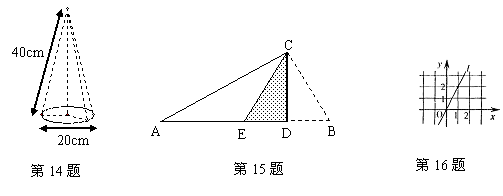A.1个 B.2个 C.3个 D.4个
三、解答题 (本大题共3小题，第17小题6分，第18、19小题各7分，共计20分)
17.当x=2006时，化简并求值
+2．
18.解方程组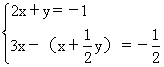
19.将一张矩形纸片沿对角线剪开后如图放置，点A、E、F、B在同一条直线上，连接DE、CF. 请你提出三个与点C有关的正确命题，并选择其中一个命题给出证明.
 |
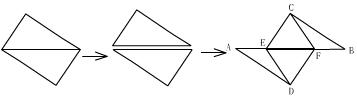四、(本大题共2小题，每小题8分，共计16分)
20.某市2006年1月公布了2005年全市各项主要经济指标的有关数据.2005年实现国内生产总值约788亿元，比2004年增长了约15%．其它数据如下表（单位：元）：
| 2001年 | 2002年 | 2003年 | 2004年 | 2005年 | |
| 农民人均纯收入 | 3464 | 3690 | 3926 | 4220 | 4750 |
根据以上数据，解答以下问题.
（1）求2004年该市国内生产总值？（精确到1亿元）
（2）请你设计一个折线图（如下图），表示2001年以来该市农民人均纯收入的发展趋势.请你根据该折线图预测该市今后两年的农民人均纯收入的变化趋势.
 |
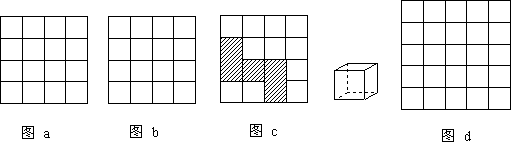
21.如果正方形网格中的每一个小正方形边长都是1，则每个小格的顶点叫做格点．
（1）在图a中以格点为顶点画一个三角形，使三角形的三边长分别为3、
、2
；
（2）在图b中以格点为顶点画一个面积为10的正方形；
（3）观察图c中带阴影的图形，请你将它适当剪开，重新拼成一个正方形；
（要求：在图c中用虚线作出，并用文字说明剪拼方法）
图c说明： .
（4）观察正方体，沿着一些棱将它剪开，展开成平面图形.若正方体的表面积为12，请你在图d中以格点为顶点画出一个正方体的平面展开图．（只需画出一种情形）
 |
五、(本大题共2小题，第22题8分，第23题9分，共计17分)
22.根据生物学家的研究，人体的许多特征都是由基因控制的，有的人是单眼皮，有的人是双眼皮，这是由一对人体基因控制的，控制单眼皮的基因f是隐性的，控制双眼皮的基因F是显性的，这样控制眼皮的一对基因可能是ff、FF或Ff，基因ff的人是单眼皮，基因FF或Ff的人是双眼皮.在遗传时，父母分别将他们所携带的一对基因中的一个遗传给子女，而且是等可能的，例如，父母都是双眼皮而且他们的基因都是Ff，那么他们的子女只有ff、FF或Ff三种可能，具体可用下表表示：
| 父亲基因为Ff | |||
| F | f | ||
| 母 亲 基因Ff | F | FF | Ff |
| f | Ff | ff | |
（1）请计算出他们的子女是双眼皮的概率；
（2）如果父亲的基因是ff，母亲的基因是FF，请用画树状图的方式求出他们的子女是双眼皮的概率.
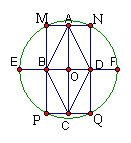
23.如图，⊙O中，BD＝10，DF＝4.顺次连结圆内接矩形各边的中点，得到菱形ABCD.
（1）求菱形ABCD的边长；
（2）顺次连结图中四点，所得到的四边形中，还有菱形吗（不再添加其它字母）？若有，请求出该菱形的边长；若没有，请说明理由.
 |
六、(本大题共2小题，第24题9分，第25题10分，共计19分)
24.水果批发市场内有一种水果，保鲜期一周，如果冷藏，可以延长保鲜时间，但每天仍有一定数量的这种水果变质，假设这种水果保鲜期内的个体重量基本保持不变.现有一个体户，按市场价收购了这种水果200千克放在冷藏室内，此时市场价为每千克2元，据测算，此后这种鲜水果每千克的价格每天可上涨0.2元，但存放一天需各种费用20元，日平均每天还有1千克变质丢弃.
(1)设x天后每千克鲜水果的市场价为y元，写出y关于x的函数关系式；
(2)若存放x天后将鲜水果一次性出售，设鲜水果的销售总金额为w元，写出w关于x的函数表达式；
(3)该个体户将这批水果存放多少天后出售，可获最大利润Q?最大利润Q是多少?
(不要求写出自变量x的取值范围)
25.如图，已知抛物线
的图象与x轴交于A、C两点.
（1）若抛物线
关于x轴对称，求
的解析式；
（2）若点B是抛物线
上一动点（B不与A、C重合），以AC为对角线，A、B、C三点为顶点的平行四边形的第四个顶点记为D，求证：点D在上；
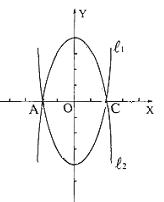（3）探索：当点B分别位于在x轴上、下两部分的图象上时，□ABCD的面积是否存在最大值或最小值？若存在，判断它是何种特殊平行四边形，并求出它的面积；若不存在，请说明理由.