中考数学辅导之—圆Ⅱ
从本次起,我们将要学习初三几何第三册的第七章《圆》,该章就所讲的知识,课文的篇幅,所涉及的知识是整个平面几何的内容,是中考所占分数最多的一章.
一、本次所学内容及内容说明
1.第一自然段主要说明
①圆的概念:此概念有2种解释
1)线段OA绕端点O旋转一周,另一个端点A随之旋转一周,所组成的图形叫圆.
2)到定点的距离等于定长的点的集合.
②圆心,半径,固定端点O叫圆心,OA的长叫半径.
作圆要两个条件:圆心确定圆的位置,圆心确定圆的大小.
③圆内部分:到定点(圆心)的距离小于定长(半径)的点的集合.
圆外部分:到定点(圆心)的距离大于定长(半径)的点的集合.
要确定一个点在圆上,圆外还是圆内,就要计算端点到圆心的距离,计算出距离与半径比较.若该距离d>r,则点在圆外,d=r,在圆上,d<r在圆内.
如⊙O的半径r=5cm,圆心O到直线l的距离d=OP=3cm.在l上有P,Q,R三点,且PD=4cm,QD>4cm,RD<4cm,则P,Q,R三点在⊙O的什么位置.
解:连结OP ∵PD=4cm OD=3cm
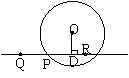由勾股定理得:OP=5cm OP=r ∴P在⊙O上
∵QD>4cm OD=3cm 连结OQ
则OQ2=OP2+QD2>25 ∴OQ>5cm ∴Q在⊙O外
用同样方法证得R在⊙O内.
④弦:连结圆上位意两点的线段,
如线段CD
经过圆心的弦叫直径
如AB(直径是圆的最大的弦)
⑤弧:圆上任意两点间的部分,弧若大于半圆叫优弧,小于半圆叫劣弧.
⑥弓形:由弦及其所对的弧组成的图形叫
弓形.弦CD与弧CD及弦CD及优弧CD所有两个弓形.
⑦同心圆:圆心相同,半径不相等的两个圆叫同心圆.
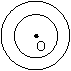⑧能够重合(或半径相等)的两个圆是等圆.
⑨在同圆或等圆中,能够互相重合的弧叫等弧。
(注意:只要说两弧是等弧,就说明这两段弧在同圆或等圆上)
2.过一点的圆有无数个,它的圆心是平面上除A外所有点.过两点的圆有无数个,它们的圆心在AB的垂直平分线上.过三点呢?若这三点不在同一直线上,过三点可以做且只可以做一个圆.(但这三点在同一直线上,则不能过三点作圆).
若把三点连结起来,构成三角形,则经过三角形各顶点的圆叫三角形的外接圆.
外接圆的圆心叫三角形外心.外心的性质是到三角形各顶点的距离相等.
三角形的外接圆的做法:作三角形两边的中垂线,两条中垂线的交点是圆心,圆心到顶点的距离是半径.
3.垂径定理:是圆中一个极重要的定理.
垂径定理:垂直于弦的直径平分弦且平分弦所对的两条弦.
推论(1):平分弦(不是直径)的直径垂直于弦,且平分弦所对的两条弦(注意括号内的条件)
(2):弦的垂直平分线经过圆心,并且平分弦所对的两条弧.
(3):平分弦所对的一条弧的直径,垂直平分弦且平分弦所对的另一条弧.
此定理和三个推论的内容是平分弦,垂直弦是直径平分弧.在这四个条件中满足两个就可得到其它两个的结论.如垂直于弦是直径得到平分弦.平分弧(垂径定理)平分弦,是直径可得到垂直弦.平分弧(推论1)垂直弦,平分弦可得到这条直径是直径,且平分弦(推论2)
注意:题设是两条,如
∵AB是直径
AB⊥CD于E
∴CE=DE
弧AC=弧DA 弧BC=弧DB
具体做题时,辅助线往往过圆心做弦的垂线段.连结圆心,则半径,弦的一半,圆心到弦的距离形成一个RtΔ,则可用勾股定理,锐角三角函数进行计算或证明.
三、本次练习:
(一)判断题
1.直径是弦.( )
2.半圆是弧,但弧不一定是半圆. ( )
3.到点O的距离等于2cm的点的集合是以O为圆心,2cm为半径的圆. ( )
4.过三点可以做且只可以做一个圆. ( )
5.三角形的外心到三角形三边的距离相等. ( )
6.经过弦的中点的直径垂直于弦,且平分弦所对的两条弧. ( )
7.经过圆O内一点的所有弦中,以与OP垂直的弦最短. ( )
8.弦的垂直平分线经过圆心. ( )
9.⊙O的半径是5,弦AB∥CD,AB=6,CD=8,则两弦间的距离是1. ( )
10.在半径是4的圆中,垂直平分半径的弦长是
.( )
11.任意一个三角形一定有一个外接圆且只有一个外接圆. ( )
(二)填空题:
1.若圆的半径是2cm,一条弦长是,则圆心到该弦的距离是______.
2.在⊙O中,弦AB为24,圆心到弦的距离为5,则⊙O的半径是______cm.
3.若AB是⊙O的直径,弦CD⊥AB于E,AE=9cm,BE=16cm,则CD=______cm.
4. 若⊙O的半径是13cm,弦AB=24cm,弦CD=10cm,AB∥CD,则弦AB与CD之间的距离是______cm.
5. ⊙O的半径是6,弦AB的长是6,则弧AB的中点到AB的中点的距离是______.
6.
如图:⊙O的直径AB⊥CD于P,
AP=CD=4cm,则OP=______cm.
7. 已知⊙O中,AB是弦,CD是直径,且CD⊥AB于M.⊙O的半径是15cm,OM:OC=3:5,则AB=______.
8.
已知O到直线l的距离OD是
cm,l上一点P,PD=
cm.⊙O的直径是20,则P在⊙O______.
(三)证明题:
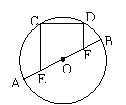
1.如图:AB是⊙O的直径,CD是弦
CE⊥CD于C,DF⊥CD于D
求证:AE=BF
2.⊙O和⊙O1相交于A,B.过A做CAD∥OO1
求证:CD=2OO1
参考答案
(一)判断题:
1.√ 2.√ 3.√ 4.× 5.× 6.×
7.√ 8.√ 9.× 10.× 11.√
(二)填空题:
1.1
2.13 3.24 4.7或17 5.
6.
7.24cm 8.⊙O上
(三)1.提示:过O做OM⊥CD于M
2.过O做OE⊥CD于E,过O1做O1F⊥CD于F.