中考数学辅导之—直线和圆的位置关系(一)
一、学习目标：
1．理解直线和圆相交，相切，相离的概念，掌握直线和圆的位置关系的判定和性质。
2． 掌握切线的判定和性质，并能应用它们证明有关问题。
3． 会用尺规作三角形的内切圆，掌握三角形和多边形的内切圆、圆的外切三角形和圆的外切多边形、三角形内心的概念。
二、基本内容及应注意的问题：
1． 在切线的定义中，要准确理解“直线和圆有唯一公共点”的含义，它是指有一个并且只有一个公共点，与“直线和圆有一个公共点”的含义不同，避免出现“直线和圆有一个公共点时叫直线和圆相切”的错误。
2．
由直线和圆的三种位置关系可以直观的得到圆心到直线的距离
与圆半径
的数量关系：
(1)
直线
和⊙Ｏ相交Û＜，
(2)
直线和⊙Ｏ相切Û＝，
(3)
直线和⊙Ｏ相离Û＞；
这三个结论，既可以作为直线和圆的各种位置关系的判定，又可作为性质。
3． 直线和圆的位置关系既可以用它们的交点的个数来区分，也可以用圆心到直线的距离与圆的半径的大小来区分，两种方式是一致的。
4． 对于切线的判定定理，必须分清定理的题设和结论，“经过半径的外端”和“垂直于这条半径”这两个条件缺一不可，否则便不是圆的切线。
5． 切线的性质有一个定理和两个推论，其中定理用途较广泛，必须熟练掌握。实际上，(1) 垂直于切线；(2) 过切点；(3) 过圆心。这三个条件中，知道任意两个，就可以得出第三个。
6． 在运用切线的判定和性质定理时，常常需要添加辅助线，一般规律为：
(1) 已知一条直线是某圆的切线时，切点的位置一般是确定的。在写已知条件时，应交待直线和圆相切于哪一点，辅助线常常是连结圆心和切点，得到半径，从而得出“切线垂直于半径”的结论。
(2) 要证明某直线是圆的切线时，如果已知直线过圆上某一点，则可以作出这一点的半径，证明直线垂直于半径；如果直线与圆的公共点没有确定，常常过圆心作直线的垂线，证明圆心到直线的距离等于半径。
7． 判定一条直线是圆的切线有三种方法：
(1) 和圆有且只有一个公共点的直线是圆的切线；
(2) 和圆心距离等于该圆半径的直线是圆的切线；
(3) 过半径的外端且垂直于这条半径的直线是圆的切线。
其中(1) 是切线的定义；(2) 和(3) 本质相同，表达形式不同。解题时，可根据题目的特点选择适当的判定方法。
8． 切线的性质主要有如下五个：
(1) 切线和圆有且只有一个公共点；
(2) 切线和圆心的距离等于该圆的半径；
(3) 圆的切线垂直于过切点的半径；
(4) 经过圆心垂直于切线的直线必过切点；
(5) 经过切点垂直于切线的直线必过圆心。
其中，(1) 是切线的定义；(2) 是判定方法的逆命题；(3)、(4)、(5)即为课本上的性质定理及其推论。
9． 任意三角形都有且只有一个内切圆（因为圆心是唯一确定的，半径只有一个定长），而任意多边形不一定有内切圆。
10．三角形的内心是用“三角形的内切圆的圆心”来定义的，由于三角形的内心就是三角形三个内角平分线的交点，所以当三角形的内心已知时，过三角形顶点和内心的射线，必平分三角形的内角。
三、例题：
例1．
已知：如图（1）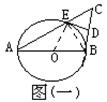
AB是⊙O的直径，CB⊥AB，AC交⊙O于E，D是的BC的中点，
求证：直线DE是⊙O的切线。
证明：连结OE、BE，
∵AB是⊙O的直径，∴∠AEB=90O，
∴BE⊥AC，则∠BEC=90O，
又∵D是BC的中点，
∴DE=BD=
BC，∴∠DBE=∠DEB
∵OE=OB ∴∠OBE=∠OEB
因此：∠DBE+∠OBE=∠DEB+∠OEB
即：∠OED=∠OBD
∵BC⊥AB 即：∠OBD=90O
∴∠OED=90O
则DE是⊙O的切线。
评析：(1) 此例是由直径、圆周角、直角三角形斜边上的中线、切线的判定等知识构成的命题。(2) 证一条直线是圆的切线,常用的两个判定方法是：直线过圆上一已知点时，作过这点的半径转证直线垂直于这条半径；直线和圆的公共点的位置未知时，过圆心作到直线的距离，转证此距离等于圆的半径。此例显然用的是第一种方法。（3）此题的分析思路：要证DE是圆的切线，而E在圆上，据圆的切线的定义则E是切点，所以应连结OE，转证DE⊥OE。
例2． 已知：如图（2）所示，在直角梯形ABCD中，AD⊥CD于D，BC⊥CD于D，且AD+CB=AB，以斜腰AB为直径作⊙O，
求证：CD是⊙O的切线。
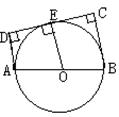图（2）
分析：要证CD是⊙O的切线，切点在什么位置呢？无法判定，因此应该用证明切线的第二种方法，作圆心到直线的距离OE，转而证OE等于圆的半径。
证明：过O作OE⊥CD于E，
∵AD⊥CD，BC⊥CD
∴ADOEBC
∵O是AB中点，则E是CD中点。
∴OE是梯形ABCD的中位线，
∴OE=(AD+BC)
又∵AD+BC＝AB
∴OE=AB。
则DC是⊙O的切线。
例3． 如图（3）所示，在直角梯形ABCD中，∠A=∠B=90O，E为AB上的一点，ED平分∠ADC，EC平分∠BCD。
求证：以AB为直径的圆与DC相切。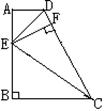
图（3）
分析：要证以AB为直径的圆与DC相切，只需证AB的中点到DC的距离等于AB。
证明：过点E作EF⊥CD于F。
ED平分∠ADC
DA⊥EA于A ÞEA=EF E为AB中点
EF⊥DF于F Þ
同理可证：EF=EB
EF=AB
Þ以AB为直径的圆与CD相切。
例4． 如图（3）所示，已知△ABC中，以AB为直径作⊙O交BC于D，过D作⊙O的切线FE，交AC于E，且AE⊥DE。
求证：AB=AC
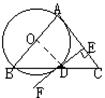图（4）
证明：连结OD
∵DE切⊙O于D，则OD⊥DE
∵AE⊥DE， ∴OD∥AC 则∠C=∠ODB
∵OB=OD ∴∠B=∠ODC
∴∠B=∠C 则AB=AC
例5．
已知：如图（5）所示，△ABC是⊙O的内接三角形，∠BAC的平分线交
于D，过D的切线分别交AB、AC的延长线于E、F，
求证：BCEF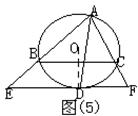
证明：连结OD
∵EF切⊙O于D， ∴EF⊥OD
∵AD平分∠BAC ∴∠BAD=∠CAD
则
由垂径定理，知：OD⊥BC
∴BC∥EF
注：此证法运用切线的性质比较灵活巧妙，只要在已知切线时用垂直方法的意识强，则不难想到。
例6．
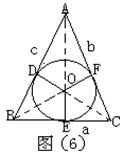
如图（6）所示，△ABC三边长为
，
，
，面积为S，内切圆⊙O的半径为，⊙O与△ABC的三边相切于D、E、F。
求证：
分析：要证，只需证：
。
证明：连结OA、OB、OC
∵⊙O切△ABC的三边于D、E、F
∴OD⊥AB，OE⊥BC，OF⊥AC
∴S△AOB=OD·AB=
同理可得：S△BOC=
S△AOC=
∴S=S△AOB+S△BOC+S△AOC=
∴
注：若∠C=90O，则有：
。
四、练习及作业：
1． 填空题：
(1)
已知圆的直径为13
，直线与圆心的距离为，当
时，直线与圆
；当
时，直线与圆 。
(2)
R
△ABC中，∠C=90O，AC=3,BC=4，则以C为圆心，
为半径的圆与AB相切；以C为圆心，
为半径的圆与AB相交。
(3) 若直线与圆的公共点个数不小于1，则直线与圆的位置关系是 。
(4) 如图（7），A为⊙O的半径OC的延长线上一点,且CA=OC，弦BC=OC，则BC= OA，∠OBA= O ，BA与⊙O的位置关系是 。
图(7)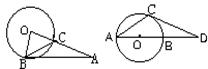
图(8)
(5) 如图（8），已知AB是⊙O的直径，延长AB到D，使BD=OB，DC切⊙O于C，则∠D= O，∠C= O。若⊙O的半径为R，则AC= 。
(6)
两个同心圆的半径分别为1和2，大圆的弦AB与小圆相切，则AB= 。
(7) 已知I为△ABC的内心，∠B=50O，则∠AIC= 。
(8) 等边三角形内切圆半径与外切圆半径之比是 。
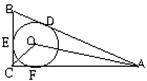
(9)
如图（9），⊙O内切于R△ABC，∠C=90O，D、E、F为切点，若∠AOC=120O，则∠OAC= O，∠B= O，若AB=2，△ABC的外接圆半径= ，内切圆半径=。
2． 选择题
(1) 设⊙O半径为，点O到直线I的距离为，若⊙O与至多只有一个公共点，则与的关系为（ ）
(A)
≥ (B)
＜ (C)
≤ (D)
=
(2) 等腰△ABC的腰AB=AC=4，若以A为圆心，2为半径的圆与BC相切，则∠BAC的度数为（ ）
(A) 30O (B) 60O (C) 90O (D) 120O
(3) 下列直线中能判定为圆的切线的是（ ）
(A) 与圆有公共点的直线。
(B) 垂直于圆的半径的直线。
(C) 过圆的半径的外端的直线。
(D) 到圆心的距离等于该圆的半径的直线。
(4) AB是⊙O的切线，在下列给出的条件中，能判定AB⊥CD的是（ ）
(A) AB与⊙O相切于直线CD上的点C。
(B) CD经过圆心O。 (C) CD是直线。
(D) AB与⊙O相切于C，过圆心O。
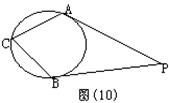
(5) 如图（10），PA、PB分别切⊙O于A、B，∠P=70O，则∠C（ ）
(A) 70O (B)55O (C)110O (D)140O
五、答案
1．
（1）相离，相切； （2）
，大于；
（3）
相切或相交； （4），90，相切；
（5）30，120，
； （6）
； （7）115
（8）
1：2； （9）15，60，
，1，
。
2．（1）A； （2）D （3）D （4）D （5）B