中考数学每日一卷之综合练习(一)
一、选择题：
1.已知直角三角形中30°角所对的直角边长是3cm，则斜边的长是：
A.3cm B.6cm C.8cm D.10cm
2.两个相似三角形中线的比是1:3，则它们的面积比是：
A.1:
B.1:3 C.:3
D.1:9
3.顺次连结梯形四边中点所得四边形是：
A.平行四边形 B.菱形 C.矩形 D.正方形
4.在Rt△ABC中，∠ACB=90°，CE⊥AB， C
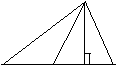CD是中线，∠B=60°，AC=
，
则DE等于：
A.2 B.2
C.
D.
A D E B
5.三角形三条边长为
的取值范围是：
A.
>4
B.>3
C.>2
D.>1
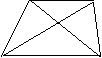6.在梯形ABCD中AD∥BC，且AD=2，
A D
BC=4，AC=3，BD=3，则∠DBC等于：
A.30° B.45° C.60° D.75° B C
7.
在 ABCD中，E在BC上，AE交
A
D
BD于F，且
，则
等于：
F
A.2:3 B.4:9 C.9:4 D.3:2 B E C
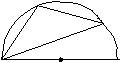
8.如图，AB是半圆O的直径，
D
∠BAC=20°，D是AC上一点， C
则∠D等于：
A.90° B.100° C.110° D.120° A O B
9.圆内相交两弦，一弦长8cm且被交点平分，另一弦被交点分成1:4，则另一弦长是：
A.2cm B.8cm C.10cm D.16cm
10.如图：⊙O半径是16，点A，B，C
在⊙O上且四边形OABC是 O
菱形，则菱形面积是： A C
A.128 B.256 C.128
D.512 B
二、填空题：
11.点P(-3，5)到
轴的距离是_______。
12.正三角形的内切圆和外接圆的面积比是_______。
13.两圆只有三条公切线则两圆的位置关系是_______。
14.函数
的图象与
轴的交点是_______。
15.直角三角形两直角边长分别是
，则斜边的长是_______。
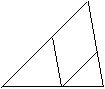
16.如图：菱形ANMP内接于△ABC，AB=21cm，BC=18cm，AC=15cm，则菱形的周长是_______。 A
 |
N
P
B M C
17.矩形ABCD截去正方形BCEF，
D E C
且矩形ABCD∽矩形AFED，若AB=m，
则BC=_______。
A F B
18.若正三角形和正六边形面积相等，则它们的边长比是_______。
三、作图题：
19.已知：线段a，∠
a
求作：等腰△ABC，使AB=AC，
∠B=∠，BC边上的高为a
四、解答下列问题：
20.关于的方程
有两个实数根，求m的取值范围。
21.为了考察甲，乙两种小麦的长势，分别从中抽取10株苗，测得苗高如下：
甲：12、13、14、15、10、16、13、11、15、11
乙：11、16、17、14、13、19、6、8、10、16
(1)计算小麦的平均苗高；
(2)哪种小麦苗高比较整齐？
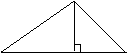22.已知△ABC中，∠B=30°，
A
∠C=45°，AC= AD⊥BC于D
求：AB和BC的长。 B D C
23.先化简后求值，其中
24.甲乙两班参加“手拉手”活动，甲班捐款200元，乙班30人捐款200元，这样两班人均捐款比甲班人均捐款多1元，问甲班有多少人参加(不超过60人)。
25.如图AC是矩形ABCD的对角线， A D
E，F在AC上，且∠1=∠2，DF交AB
延长线于P E F 2
求证：(1)△ABE≌△CDF 1
(2)
B
C
P
26.已知抛物线
轴有两个交点且对称轴为直线=3，
(1)求：抛物线与轴的交点坐标和顶点坐标；
(2)若点P的坐标为(1,-5)，它关于轴的对称点是否在抛物线上。
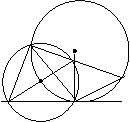27.如图：⊙O，⊙
交于A，B
两点，PA切⊙于A交⊙O于P，
B
A交⊙O于Q，BQ交⊙于C
Q C
求证：(1)PQ∥AC O
(2)PQ·AC=2AO·AQ P A
(3)PQ·AC=AQ2+BQ·CQ
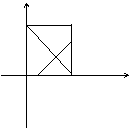28.如图：过点A(2,4)分别向
轴
y
作垂线，垂足为M，N，点P在轴上由O
N
A(2,4)
点出发，沿OM运动，1分钟到达M点，点 Q
Q在MA上沿MA方向运动，1分钟到达A点
(1)经过多少时，线段PQ的长度为2； O P M x
(2)设PQ长的平方
的函数关系；
(3)当
取何值时PQ⊥MN。
练习答案
一、选择题：
1.B 2.D 3.A 4.B 5.C 6.A 7.B 8.C 9.C 10.C
二、填空题：
11. 5 12. 1:4 13. 外切 14. (0,
) 15.
4
16. 35 17. 
18.
三、作图题：
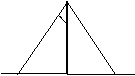19.提示：先做线段AD=a，过D做直线MN⊥AD，
A
以AD为一边，A为顶点做∠DAB=90°-，交
MN于B，完成图形。
N M
B D C
四、20.解：Δ=（-m）2 -4*2*（-30）=m2+240
∵m2≥0 ， ∴m2 +240>0 ， 即：Δ>0
∴不论m取什么值，方程都有两个实数根，且两根不等。
因此，m的取值范围是全体实数。
21.解：
∵
∴甲种小麦苗高比较整齐。
22.解：AB=4，BC=
23.解：原式=
=
=
当时，原式=
24.解：设甲班人，由题意得
解得：
经检验
都是原方程的根，但=120不合题意舍去。
答：甲班50人。
25.略
26.∵对称轴
，∴ 
即：
，∴ 
∴抛物线是
①与轴交点是(0,0)和(6,0)，顶点坐标是(3,-9)
②P(1,-5)关于轴的对称点是(1,5)
把
代入
左边=5，右边=-5 左边≠右边
∴P(1,-5)关于轴的对称点不在抛物线上。
27.28.题同学考虑。