中考数学模拟试卷(二)
(满分:150分 时间:120分钟)
一、选择题(本题共12小题,下列各小题的四个选项中,只有一个符合题意.每小题3分,共36分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
1.如果零上5℃记作+5℃,那么零下5℃记作
A.-5 B.-10 C.-10℃ D.-5℃
2.下列各式中错误的是
A.(a-2)3=a-6 B.(a2)3=a5
C.a2÷a3=a-1 D.a2×a3=a5
3.若点P(1-m,m)在第二象限,则下列关系式中,正确的是
A. 0<m<1 B. m<0 C. m>0 D. m>1
4.小明从正面观察下图所示的两个物体,看到的是
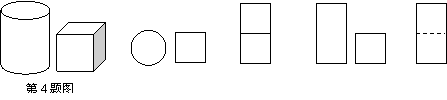 |
A. B. C. D.
5.下列美丽的图案,既是轴对称图形又是中心对称图形的个数是

A.1个 B.2个 C.3个 D.4个
6.如图,小明周末到姑姑家,走到十字路口,记不清哪条路通往姑姑家,那么他能一次选对路的概率
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.如图,在□ABCD中,对角线AC,BD相交于点O,E,F是对角线AC上的两点,当E,F满足下列哪个条件时,四边形DEBF不一定是平行四边形
A.AE=CF B.DE=BF C.∠ADE=∠CBF D.∠AED=∠CFB
C.∠ADE=∠CBF D.∠AED=∠CFB
8.某服装店以每套a元的价格购进100套西服,然后将进价提高20%作为销售价,销售50套后,余下部分按销售价的8折出售,售完后获得的利润是
A.6a元 B.8a元 C.10a元 D.12a元
9.反比例函数![]() 的图象在
的图象在
A.第一、三象限 B.第二、四象限 C.第一、二象限 D.第三、四象限
10.二次函数y=2x2+8x+9的顶点坐标
A.(-2,1) B.(2,1) C.(2,-1) D.(1,2)
11.如图,AD是△ABC的中线,∠ADC=60°,BC=4 cm,把△ADC沿直线AD折叠后,点C落在点C′,那么BC′的长为
A.1cm B.![]() cm C.2cm D.
cm C.2cm D.![]() cm
cm
12.某人才市场2006年上半年应聘和招聘人数排名前5个类别的情况如下图所示,
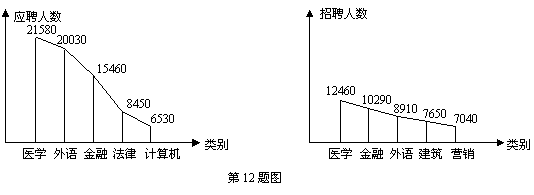
若用同一类别中应聘人数与招聘人数比值的大小来衡量该类别的就业情况,则根据图中信息,下列对就业形势的判断一定正确的是
A.医学类好于营销类 B.金融类好于计算机类
C.外语类最紧张 D.建筑类好于法律类
二、填空题(本题共6小题,每小题4分,共24分)
13.写出一个自变量的取值范围是x>3的函数解析式: .
14.因式分解:3x2-12xy+12y 2= .
 15.某商场5月份随机抽查了7天的营业额,结果分别如下
15.某商场5月份随机抽查了7天的营业额,结果分别如下
(单位:万元):3.6,3.2,3.4,3.9,3.0,3.1,3.6.试估计该
商场5月份(31天)的营业额大约是 万元.
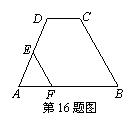
16.如图,梯形ABCD中,AB∥CD,E是AD的中点,EF∥CB
交于F,BC=4cm,则EF= cm.
17.如果△+△=★,○=□+□,△=○+○+○+○,那么★÷□= .
18.我们来探究 “雪花曲线”的有关问题:下图(1)是边长为1的正三角形,将此正三角形的每条边三等分,而以居中的那一条线段为底边再作正三角形,然后以其两腰代替底边,得到第二个图形如下图(2);再将下图(2)的每条边三等分,并重复上述的作法,得到第三个图形如下图(3),如此继续下去,得到的第五个图形的周长应等于 .

三、解答题(解答应写出必要的计算过程、推演步骤或文字说明,共90分)
19.(本题满分6分)
计算:![]()
20.(本题满分6分)
解方程组: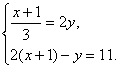
21.(本题满分8分)
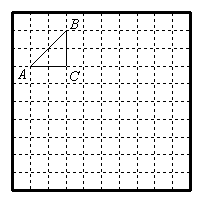
如图是一个10×10格点正方形组成的网格,△ABC是格点三角形(顶点在网格交点处),请你在图中画出与△ABC相似的格点△A1B1C1和△A2B2C2,且△A1B1C1与△ABC的相似比是2,△A2B2C2与△ABC的相似比是![]() .
.

22.(本题满分8分)
阅读材料:大数学家高斯在上学读书时曾经研究过这样一个问题:
1+2+3+…+100=?经过研究,这个问题的一般性结论是1+2+3+…+n
=![]() ,其中n是正整数.
,其中n是正整数.
现在我们来研究一个类似的问题:1×2+2×3+…+![]() =?
=?
观察下面三个特殊的等式:1×2=![]() (1×2×3-0×1×2)
(1×2×3-0×1×2)
2×3=![]() (2×3×4-1×2×3)
(2×3×4-1×2×3)
3×4=![]() (3×4×5-2×3×4)
(3×4×5-2×3×4)
将这三个等式的两边相加,可以得到1×2+2×3+3×4=![]() ×3×4×5=20.
×3×4×5=20.
读完这段材料,请你思考后回答:
1×2+2×3+…+10×11= ;
1×2+2×3+…+![]() = .
= .
 23.(本题满分8分)
23.(本题满分8分)
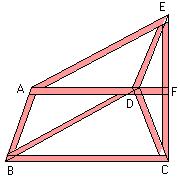
如图,是某城市部分街道示意图,AF∥BC,EC⊥BC,BA∥DE.BD∥AE.甲、乙两人同时从B站乘车到F站.甲乘1路车,路线是B—A—E—F;乙乘2路车,路线是B—D—C—F.假设两车速度相同,途中耽误时间相同,那么谁先到达F站.请说明理由.
24.(本题满分10分)
甲骑自行车、乙骑摩托车沿相同路线由A地到B地,行驶过程中路程与时间的函数关系的图象如图.根据图象解决下列问题:
(1)分别求出甲、乙两人的行驶速度;
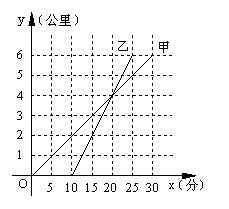 (2)在什么时间段内,两人均行驶在途中(不包括起点和终点)?在这一时间段内,请你根据下列情形,分别列出关于行驶时间x的方程或不等式(不化简,也不求解):① 甲在乙的前面;② 甲与乙相遇;③ 甲在乙后面.
(2)在什么时间段内,两人均行驶在途中(不包括起点和终点)?在这一时间段内,请你根据下列情形,分别列出关于行驶时间x的方程或不等式(不化简,也不求解):① 甲在乙的前面;② 甲与乙相遇;③ 甲在乙后面.
25.(本题满分10分)
 周日,刚学过解直角三角形的小岩打算去测量河对岸的烟囱高度,他先向老师借了两块木制大三角板,站在地上的C点,测得顶点A的仰角是30°,接着又向前走20米到达D地(C,D,B在同一条直线上),测得顶点A的仰角是45°,又知测量时三角板平行于地面的一边到地面的距离始终为1.2米(如图),于是他就计算出了烟囱的高度,你能把小明的计算过程与结果写出来吗?(结果可保留根号)
周日,刚学过解直角三角形的小岩打算去测量河对岸的烟囱高度,他先向老师借了两块木制大三角板,站在地上的C点,测得顶点A的仰角是30°,接着又向前走20米到达D地(C,D,B在同一条直线上),测得顶点A的仰角是45°,又知测量时三角板平行于地面的一边到地面的距离始终为1.2米(如图),于是他就计算出了烟囱的高度,你能把小明的计算过程与结果写出来吗?(结果可保留根号)
26.(本题满分10分)
两人同去某风景区游玩, 每天某一时段开往该风景区有三辆汽车(票价相同),但是他们不知道这些车的舒适程度, 也不知道汽车开过来的顺序. 两人采用了不同的乘车方案:
甲无论如何总是上开来的第一辆车. 而乙则是先观察后上车, 当第一辆车开来时, 他不上车, 而是仔细观察车的舒适状况, 如果第二辆车的舒适程度比第一辆好, 他就上第二辆车; 如果第二辆车不比第一辆好, 他就上第三辆车.如果把这三辆车的舒适程度分为上、中、下三等, 请尝试着解决下面的问题:
(1) 三辆车按出现的先后顺序工有哪几种不同的可能?
(2) 你认为甲、乙采用的方案, 哪一种方案使自己乘上等车的可能性大? 为什么?
27.(本题满分12分)
某“研究性学习小组”遇到了以下问题,请参与:
已知,△ABC是等边三角形且内接于⊙O,取弧AB上异于A、B的点M.设直线CA与BM相交于点K,直线CB与AM相交于点N.
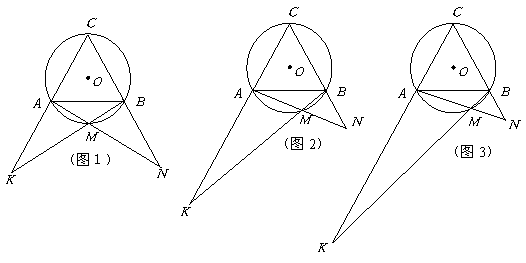 (1)如图1、图2、图3,M分别为弧AB的中点、三分之一点、四分之一点,△ABC的边长均为2,分别测量出AK、BN的长,计算AK·BN的值(精确到0.01)并将结果填入下表中:
(1)如图1、图2、图3,M分别为弧AB的中点、三分之一点、四分之一点,△ABC的边长均为2,分别测量出AK、BN的长,计算AK·BN的值(精确到0.01)并将结果填入下表中:

| △ABC的边长 | AK·BN的值 | |
| 图1 | 2 | |
| 图2 | 2 | |
| 图3 | 2 |
(2)如图4,当M为弧AB上任意一点时,根据(1)的结果,猜想AK·BN与AB的数量关系式为 ;
(3)对(2)中提出的猜想,依图4给出证明.
28.(本题满分12分)
已知:如图,在直角梯形ABCD中,AD∥BC,BC=5cm,CD=6cm,∠DCB=60°,∠ABC=90°.等边三角形MPN(N为不动点)的边长为acm,边MN和直角梯形ABCD的底边BC都在直线l上,NC=8cm,将直角梯形ABCD向左翻折180°,翻折一次得图形①,翻折二次得图形②,如此翻折下去.
(1)将直角梯形ABCD向左翻折二次,如果此时等边三角形的边长a≥2cm,那么这时两图形重叠部分的面积是多少?
(2)将直角梯形ABCD向左翻折三次,如果第三次翻折得到的直角梯形与等边三角形重叠部分面积等于直角梯形ABCD的面积,那么这时等边三角形的边长a至少应为多少?
 (3)将直角梯形ABCD向左翻折三次,如果第三次翻折得到的直角梯形与等边三角形重叠部分面积等于直角梯形ABCD面积的一半,那么这时等边三角形的边长至少应为多少?
(3)将直角梯形ABCD向左翻折三次,如果第三次翻折得到的直角梯形与等边三角形重叠部分面积等于直角梯形ABCD面积的一半,那么这时等边三角形的边长至少应为多少?
