中考数学辅导之—反比例函数及圆相关公式
反比例函数.圆周长、弧长公式及圆的面积和扇形、弓形面积.
一、教学目的:
1.掌握反比例函数的定义、图象和性质.
2.掌握圆周长、弧长公式及圆、扇形、弓形的面积公式.并能熟练的进行公式变形、正确的计算.
二、基础知识及说明:
1.函数![]() 叫反比例函数(或
叫反比例函数(或![]() ).其图象是双曲线,所以我们也叫双曲线
).其图象是双曲线,所以我们也叫双曲线![]() .当
.当![]() 时,图象在一、三象限,在每个象限内,
时,图象在一、三象限,在每个象限内,![]() 的增大而减小,当
的增大而减小,当![]() ,双曲线在二、四象限, 在每个象限内,
,双曲线在二、四象限, 在每个象限内,![]() 的增大而增大.
的增大而增大.
2.设圆的半径是![]() ,则圆的周长
,则圆的周长![]() .若一条弧所对的圆心角是
.若一条弧所对的圆心角是![]() ,半径是R,则弧长公式是
,半径是R,则弧长公式是![]() .(注意,求弧长有①圆心角的度数②半径的长两个条件),注意公式的变形.已知弧长求圆心角
.(注意,求弧长有①圆心角的度数②半径的长两个条件),注意公式的变形.已知弧长求圆心角![]() .已知弧长求半径R=
.已知弧长求半径R=![]()
![]() .
.
3.已知圆的半径R,则圆的面积是S=![]() R2.扇形的面积是
R2.扇形的面积是![]() ,第一个公式是利用圆心角的度数
,第一个公式是利用圆心角的度数![]() 和半径R求得的.第二个公式是利用扇形的弧长和半径R求得的,要注意根据已知条件选用恰当的公式.
和半径R求得的.第二个公式是利用扇形的弧长和半径R求得的,要注意根据已知条件选用恰当的公式.
4.弓形面积,若一个弓形小于半圆则S弓形=S扇形-S△;若一个弓形大于半圆,则S弓形=S扇形+S△.
三、练习:
1.填空题:
![]() ⑴弧AB的长是10cm,半径是10cm,则AB所对的圆心角是____度, S扇形AOB=____cm2.
⑴弧AB的长是10cm,半径是10cm,则AB所对的圆心角是____度, S扇形AOB=____cm2.
⑵两个同心圆,若小圆的切线被大圆截取的部分为8cm,则两圆围成的环形面积是____cm2.
⑶扇形的圆心角是120°,弧长是4![]() ,则扇形的面积是____.
,则扇形的面积是____.
⑷弓形的弧所对的圆心角是120°,弓形的弦长是![]() ,则该弓形的面积是____.
,则该弓形的面积是____.
 ⑸如图:两个同心圆被两条半径截得 C
⑸如图:两个同心圆被两条半径截得 C
![]() 的AB长是
的AB长是![]() cm. CD的长是
cm. CD的长是![]() cm.
A
B D
cm.
A
B D
AC=8cm,则S阴影=____cm2. O
⑹已知扇形的半径是它内切圆的半径的3倍,则扇形的面积与内切圆的面积之比是____.
⑺已知![]() ,
,![]() 的算术平方根成正比例,
的算术平方根成正比例,![]() 成反比例,且当
成反比例,且当![]() ,则
,则![]() 间的函数关系式是____.
间的函数关系式是____.
⑻已知![]() 与反比例函数
与反比例函数![]() 的图象的两个交点的横坐标分别是
的图象的两个交点的横坐标分别是![]() ,则这个一次函数的解析式是____.
,则这个一次函数的解析式是____.
⑼反比例函数的图象经过(-3,6)点,则这个函数的解析式是____.
⑽如图:已知⊙O1和⊙O2的半径分别是6cm和2cm,⊙O1和⊙O2外切于P.AB是两圆的外公切线,则S阴影=____cm2.
⑾已知反比例函数![]() 的图象经过点A(
的图象经过点A(![]() ),已知直线
),已知直线![]() 也经过点A与
也经过点A与![]() 轴相交于点B,且S△AOB=6,则直线
轴相交于点B,且S△AOB=6,则直线![]() 的解析式是____.
的解析式是____.
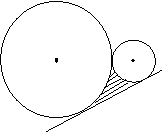 |
P
O1 O2
B
A
⑿已知反比例函数![]() 的图象在二、四象限,则
的图象在二、四象限,则![]() 的值是____.
的值是____.
⒀如果一个扇形的半径为一个圆的半径的2倍,且扇形的面积与圆的面积相等,那么这个扇形的中心角是____度.
⒁弓形的高为1cm,弦长为![]() ,则弓形的面积是____.
,则弓形的面积是____.
四、练习答案:
⑴![]()
⑵![]() (提示:S环=S大圆-S小圆=
(提示:S环=S大圆-S小圆=![]() =
=![]() =
=![]() =16
=16![]() )
)
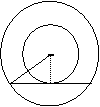
R r
⑶![]()
⑷![]() (提示:∠AOD=60° AD
(提示:∠AOD=60° AD![]()
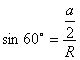 R
R![]() S扇形=
S扇形=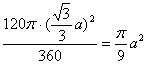 OD=
OD=![]() S△=
S△=![]() )
)
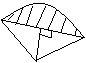
A D
B
O
⑸分析:S阴影=S大扇-S小扇,而由S扇形=![]() ,必须求R.但在此图形中,两扇形的半径不同,面积不同,但两个扇形的圆心角相同,利用
,必须求R.但在此图形中,两扇形的半径不同,面积不同,但两个扇形的圆心角相同,利用![]() .再利用
.再利用![]()
![]() 和圆心角相同即
和圆心角相同即![]() ,解得:
,解得:![]() ∴S大扇=
∴S大扇=![]() , S小扇=
, S小扇=![]()
∴S阴影=![]() .此题还可记住书中P212中第11题第②小题中公式S阴影=
.此题还可记住书中P212中第11题第②小题中公式S阴影=![]() .
.
⑹此题的图
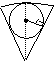 A
B
A
B
![]() D
D
O
设小圆半径为r,扇形的半径3r,圆⊙![]() 与扇形成内切 ∴O
与扇形成内切 ∴O![]() =2r OD=r
=2r OD=r
∴∠![]() OD=30°, ∠AOB=60°S扇形=
OD=30°, ∠AOB=60°S扇形=![]() ∴
∴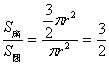 .
.
⑺![]() ⑻
⑻![]() ⑼
⑼![]()
⑽提示:连结O1O2,O1A,O2B,过O2作O2D⊥O1A,则O1O2=8cm,O1D=4cm,
则∠O1O2D=30°,∠AO1O2=60°,∠O1O2B=120°,S扇形=6![]() ,S小扇=
,S小扇=![]() ,S梯形=16
,S梯形=16![]() ,
,
S阴影=16![]() -
-![]() .
.
⑾![]() ⑿2 ⒀90°
⒁
⑿2 ⒀90°
⒁![]()