方程与方程组（2）

一、选择

1． 已知直角三角形的两条直角边的长恰好是方程的两根，则此直角三角形的斜边长为(　 ).

A.　　　　 B.3　　　　　　 C.　　　　 　　　D.13

2、一元二次方程的根的情况为（　　）

A、有两个不相等的实数根　　　　　　 B、有两个相等的实数根

C、只有一个实数根　　　　　　　　　 D、没有实数根

3。　某校初三（2）班40名同学为“希望工程”捐款,共捐款100元.捐款情况如下表：

捐款（元）	1	2	3	4
人　 数	6			7

表格中捐款2元和3元的人数不小心被墨水污染已看不清楚.

若设捐款2元的有名同学,捐款3元的有名同学,根据题意,可得方程组

A、　　　　B、　　　 C、 D、

4．某市为处理污水需要铺设一条长为4000米的管道，为了尽量减少施工对交通所造成的影响，实际施工时每天比原计划多铺设10米，结果提前20天完成任务。设原计划每天铺设管道x米，则可得方程（　　　）

（A）　　　　  （B）

 （C）　　　　　 （D）

二、填空

1、　　　  某市政府切实为残疾人办实事,在区道路改造中为盲人修建一条长3000m的盲道,根规　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 划设计和要求,该市工程队在实际施工时增加了施工人员,每天修建的盲道比原计划增加50％,结果提前2天完成,则实际每天修建盲道__________m.

2．请给出一元二次方程　　　　＝0的一个常数项，使这个方程有两个不相等的实数根。

三、解答下列各题:

1　解方程：．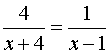

2．(本题满分12分)

某水果批发市场香蕉的价格如下表：

购买香蕉数 (千克)	不超过 20千克	20千克以上但不超过40千克	40千克以上
每千克价格	6元	5元	4元

　 张强两次共购买香蕉50千克(第二次多于第一次)，共付款264元，请问张强第一次、第二次分别购买香蕉多少千克?

3、为满足市民对优质教育的需求某中学决定改变办学条件计划拆除一部分旧校舍、建造新校舍。拆除旧校舍每平米需80元，建造新校舍每平米需700元。计划在年内拆除旧校舍与建造新校舍共7200平方米，在实施中为扩大绿化面积，新建校舍只完成了计划的80％，而拆除校舍则超过了10％，结果恰好完成了原计划的拆、除的总面积。

（1）求原计划拆建面积各多少平方米？

（2）若绿化1平方米需200元，那么在实际完成的拆、建工程中节余的资金用来绿化大约是多少平方米？

4．（本题7分）

　 苏州地处太湖之滨，有丰富的水产养殖资源，水产养殖户李大爷准备进行大闸蟹与河虾的混合养殖，他了解到如下信息：

①每亩水面的年租金为500元，水面需按整数亩出租；

②每亩水面可在年初混合投放4公斤蟹苗和20公斤虾苗；

③每公斤蟹苗的价格为75元，其饲养费用为525元，当年可获1400元收益；

④每公斤虾苗的价格为15元，其饲养费用为85元，当年可获160元收益；

  (1)若租用水面n亩，则年租金共需　　　　　　　　　　元；

　(2)水产养殖的成本包括水面年租金、苗种费用和饲养费用，求每亩水面蟹虾混合养殖的年利润(利润：收益—成本)；

　(3)李大爷现有资金25000元，他准备再向银行贷不超过25000元的款。用于蟹虾混合养殖。已知银行贷款的年利率为8％，试问李大爷应该租多少亩水面，并向银行贷款多少元．可使年利润超过35000元?

5，　活动，鼓励学生将自己的压岁钱和零花钱存入银行，

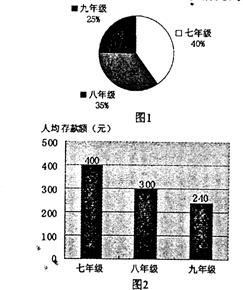定期一年，到期后可取回本金，而把利息捐给贫困失学儿童.某中学共有学生1200人，图1是该校各年级学生人数比例分布的扇形统计图，图2是该校学生人均存款情况的条形统计图.

（1）九年级学生人均存款元；

（2）该校学生人均存款多少元？

（3）已知银行一年期定期存款的年利率是2.25%　　 （“爱心储蓄”免收利息税），且每351元能提供 给一位失学儿童一学年的基本费用，那么该校一学年能帮助多少为贫困失学儿童.