九年级数学学科综合调研测试试题（一）

数学问卷

说明：

1．本试卷分为选择题部分和非选择题部分，全卷共三大题25小题，共150分．考试时间120分钟．

2．答题前，考生务必将自己的姓名、考生号、考试科目用2B铅笔涂在答题卡上．

3． 本卷分“问卷”和“答卷”，本试卷选择题部分必须填在答题卡上，否则不给分；非选择题部分的试题，学生在解答时必须将答案写在“答卷”上指定的位置（方框）内，写在其他地方答案无效，“问卷”上不可以用来答题；

4．考试结束后，考生须将本试卷和答题卡一并交回；

5．考生解答填空题和解答题必须用黑色字迹钢笔或签字笔作答，如用铅笔作答的试题一律以零分计算；

6．选择题要求用规定型号的铅笔填涂，涉及作图的题目，用题目中规定型号的铅笔作图．

7．本卷解答允许使用市教研室推荐的二款计算器．

选择题部分

一、　　　　　  选择题（本大题共10小题，每小题3分，共30分）

1．根据国家环保局通报，北京市是“十五”水污染防治计划完成最好的城市．预计今年年底，北京市污水处理能力可以达到每日吨．将用科学记数法表示为　　　　　  （　　 ）

A．1．684×10⁶吨　　 B．1．684×10⁵吨　　 ．C．0．1684×10⁷吨　　 D． 16．84×10⁵吨

2．下列运算中，错误的是　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　 ）

  A．　　  B．　　  C．　　  D．

3．=　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　 ）

  A．–3　　　　　  B．3　　　　　　　　  C． ±3　　　　　　  D．±-3

4．点P在第二象限，若该点到轴的距离是2，到轴的距离是1，则点P的坐标是 （　 　）

  A．(1，2)　　　　 B．（-2，1）　　　　　  C．(2，-1)　　　　　  D．(-1，2)

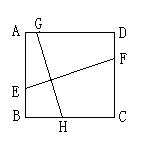5．正方形ABCD中,EF与GH都是端点分别在正方形对边上且互相垂直的两条线段(如右图)，那么下列表示EF、GH的关系中，正确的是（　　 ）

A． EF=GH　 B．　EF>GH　 C．　EF<GH　D． EF≠GH

 6．在△ABC中，∠C＝90°，若，则sinA=　　　 (　　 )

　A．　　　　 B． 　　　 C． 　　　D．

 7．如图，在半径为5cm的⊙O中，圆心O到弦AB的距离是3cm，则 弦AB的长为　　　　　　　　　　　　　　　　　　　　　　　 （　　 ）

A．　4cm　　 B． 6cm　　 C． 8cm　　　D．10cm

 8．中央电视台“幸运52”栏目中的“百宝箱”互动环节，是一种竞猜游戏．游戏规则如下：在20个商标牌中，有5个商标牌的背面注明了一定的奖金额，其余商标牌的背面是一张哭脸，若翻到哭脸就不得奖，参与这个游戏的观众有三次翻牌的机会．某观众前两次翻牌均获得了奖金，如果翻过的牌不能再翻，那么这位观众第三次翻牌获奖的概率是　　　　　　　 （　　 ）

　 

A．　　　　 B．　　　　 C．　　　　D．

 

9．下列一元二次方程中，有实数根的是　　　　　　　　　　　　　　　　　　　  （　　 ）

A． 　　 B．　　　 C．　 　　 D．　

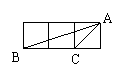
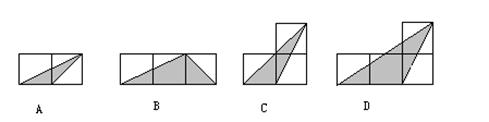
10．如图，小正方形的边长均为1，则下列图形中的三角形（阴影部分）与△ABC

相似的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　 ）

非选择题部分（共120分）

二、　　　　　  填空题（本大题共6小题，每小题3分，共18分）

 11．因式分解：=　　　　　　　　　　　　　　　 ．

 12．已知反比例函数的图像经过点P（－2，－1），则=　　　　　　　　　　　　 ．

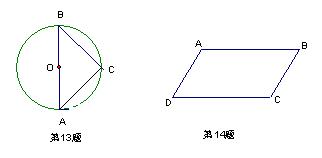
 13．如右图，AB是⊙O的直径，C是⊙O上的一点，且BC=AC，∠ABC的度数是　　　　　　　　 ．

 14．如图，AB∥CD，要使四边形ABCD是平行四边形，还需要补充一个条件：　　　　　　 　　．

 　　　　　　　　　　　　　　　　　　　 

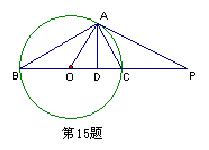
15． 如图，点P是⊙O的直径BC的延长线上一点，过点P作⊙O的 切线PA，切点为A，连结BA、OA、CA，过点A作AD⊥BC于

D，则图中共有　　　　 个直角．

16． 一跳蚤在一直线上从O点开始，第1次向右跳1个单位，紧接着第2次向左跳2个单位，第3次向右跳3个单位，第4次向左跳4个单位，……，依此规律跳下去，当它跳第100次落下时，落点处离O的距离是　　 　　个单位．

三、　　　　　  解答题（本大题共9小题，共102分）

17．（本题满分9分）化简并求值：

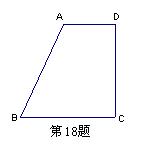18．（本题满分9分）如图，在直角梯形ABCD中，已知底边AD＝6cm ，BC=11cm，腰CD＝12 cm，求这个直角梯形的周长．

19．（本题满分10分）2005年我市春季房交会期间，某公司对参加本次房交会的消费者进行了随即问卷调查，共发放1000份调查问卷，并全部收回．根

据调查问卷，将消费者年收入的情况整理后，制成表格如下：

年收入（万元）	1．2	1．8	3．0	5．0	10．0
被调查的消费者数（人）	200	500	200	70	30

 

 将消费者打算购买住房面积的情况整理后，作出部分频数分布直方图．

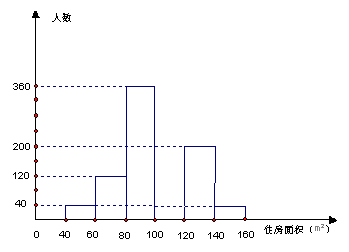　注：每组包含最小值不包含最大值，且住房面积取整数．

  请你根据以上信息，回答下列问题：

（1）　　　 根据表格可得，被调查的消费者平均年收入为　　  万元；被调查的消费者中年收

入的中位数是　　　 ；在平均数与中位数这两个数中，　　　　 更能反映被调查的消费者年收入的一般水平．

（2）　　　 根据频数分布直方图可得，打算购买100

－120m²房子的人数为　　　 人；打算购买住房面积小于100m²的消费者占被调查消费者人数的百分数是　　　　 ．

（3）　　　 在图中补全这个频数分布直方图．

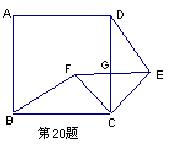
20．（本题满分10分）如图，四边形ABCD是正方形，△ECF是等腰直角三角形，CE=CF，G是CD与EF的交点．求证：△BCF≌△DCE

21．（本题满分12分）已知二次函数

　 的图像经过点（0，5）．

（1）　　　 求m的值，并写出二次函数的解析式；

（2）　　　 用配方法求出二次函数的顶点坐标和对称轴；

（3）　　　 作出该二次函数的大致图象．

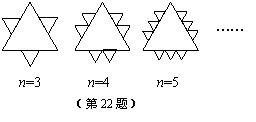22．（本大题满分12分）已知一个面积为S的等边三角形，现将其各边n（n为大于2的整数）等分，并以相邻等分点为顶点向外作小等边三角形（如图所示）．

（1）当n = 5时，共向外作出了　 　 个小等边

三角形，每个小等边三角形的面积为　 　　 ；

（2）当n = k时，共向外作出了 　　　　　  个

小等边三角形，这些小等边三角形的面积和

为　　　　　　  （用含k的式子表示）．

23．（本大题满分12分）某商场今年2月份的营业额为400万元，3月份的营业额比2月份增加10％，5月份的营业额达到了633．6万元，求3月份到5月份营业额的平均月增长率．

24．（本大题满分14分）阅读材料后回答问题：

解不等式

解：

分两种情况

①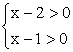 或 ②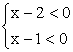　　

解不等式组①，得

解不等式组②，得

∴原不等式的解集为。

请利用上述解不等式的方法解决下面的问题。

解不等式：

25．（本大题满分14分）已知Rt△ABC中，AC=6，BC=8，∠ACB=90°，P是AB边上的动点（与点A、B不重合），Q是AC边上的动点（与点A、C不重合），如图。

（1）　　  当PQ∥BC，且Q为AC的中点时，求线段PA的长；

（2）　　  若以CQ为直径作圆D，请问圆D有没有可能与斜边AB相切？若相切请求出该圆的半径；

（3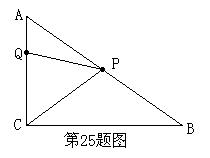）　　  当PQ与BC不平行时，△CPQ可能为直角三角形吗？若有可能，请求出线段CQ的长的取值范围；若不可能，请说明理由。

九年级数学学科综合调研测试试题（一）参考答案

一、选择题(本大题共10小题,每小题3分,共30分)

题号	1	2	3	4	5	6	7	8	9	10
答案	A	B	B	D	A	B	C	B	C	A

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　

二、填空题(本大题共6小题,每小题3分,共18分)

题号	11	12	13	14	15	16
答案		2	45°	AB=CD或AD∥BC	4	50

三、解答题(本大题共9小题 ,共102分)

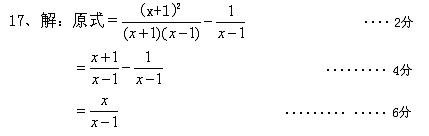
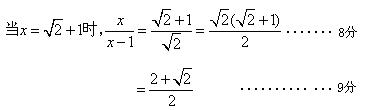
18、解：过点A作AE⊥BC ，垂足为E　　　　…………　1分　　　　  　　　　 

∴AE＝CD＝12，EC=AD＝6　　　　　　　  …………3分

 ∴BE=BC－EC=11－6=5　　　　　　　　　　 …………5分

在Rt△AEB中，

 AB＝　　　　 …………7分

∴直角梯形ABCD的周长＝

AB+BC+CD+DA=13+11+12+6= 42 (cm)　　　　 …………9分

19、　（1）2.39…………1分，1.8……………2分，中位数……………………3分；

（2）240　　………………5分，　　52％　　　　　　………………7分；

（3）略　　　　　　　　　　　　　　　　　　………………………10分

　

21、解：（1）∵ 二次函数 的图像经过点（0，5）.

　　　　　  ∴ m+2=5

　　　　　  ∴ m=3　　　　　　　　　　　　　　　　　…………　２分　

　　　　　  ∴ 二次函数解析式为：　　　…………　４分

　　 

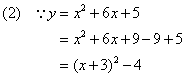
…………　５分　

　　　　  ∴顶点坐标为（－3，－4）　　　　　　　　　　…………　７分　

　　　　　  对称轴是直线　　　　　　　　　　 　…………　９分　

　　　（３）建立正确坐标系　　　　　　　　　　　　 　…………　1０分　

　　　　　　作出正确图象(作图略)　　　　　　　　　 　…………　1２分　

2２、解：（1）9，．（每个答案各3分）　　…………………………………6分

　 （2）3（k－2），． （每个答案各3分） …………………………12分

2３、解：设3月份到5月份营业额的平均月增长率为x，　　　　…………　1分　

依题意得， 400(1+10％)(1+x)² = 633.6　　　　　　　　　 …………　４分　

　　　　  440(1+x)² =633.6

　　　　 (1+x)² =1.44 　　　　　　　　　　　　　　　　…………　６分　

　　　　∴1+x = ±1.2　　　　　　　　　　　　　　　　…………　８分　

　　　 ∴x₁ = 0.2　,　x₂ = －2.2（不合题意，舍去）　 　…………　1０分　

答：3月份到5月份营业额的平均月增长率是20％. 　　　　　  …………　1２分　

2４、解：

　　　　　　　　　　　　　　　  …………　２分　

分两种情况

①　　　　　　　　　　　　　　　　　　　  …………　5分　

或

②　　　　　　　　　　　　　　　　　　　  …………　8分　

解不等式组①，得　　　　　　　　　　  　 …………　10分　

解不等式组②，无解　　　　　　　　　　　　　　　 …………　1２分　

∴原不等式的解集为。　　　　　　　　　　 …………　14分　

25、解：（1）当PQ∥BC，且Q为AC中点时，

　　 PQ是△ABC的中位线　　　　　　　　　　　　　　　 …………　1分

∴　　　　　　　　 　　　　　　　　　…………　2分

∵AC=6　∴　　　　　　　　　　　　  …………　3分

∴　　　　　　　　 …………　4分

（2）以CQ为直径作圆D，圆D可以与AB相切。　　　 …………　5分

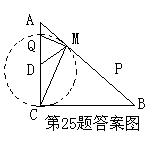当圆D与AB相切时，设切点为M，连结DM，则DM⊥AB，且Rt△ADM ∽Rt△ABC；　　　　  …………　6分

设CD=，则DM=，DB=6-。 …………　7分

由　　  …………　8分

解得

即圆D的半径为。　　　　  …………　9分

（3）当PQ与BC不平行时，只有∠CPQ＝90°时，

△CPQ才可能为直角三角形。　　　　　　  　　　　　　　 …………　10分

①当，且点P运动到点M的位置时，△CPQ为直角三角形。　　　　　　　　　　　　　　　　　　　　　　　　　  ………　11分

②当时，圆D与直线AB有两个交点，当点P运动到这二个交点的位置时，△CPQ为直角三角形。　　　　　　　　　　　　　　  　　　　　…………　12分

③当时，圆D与直线AB相离，没有交点，即点P在AB上运动时都在圆外，∠CPQ<90°此时△CPQ不可能为直角三角形。　　　　　　　 …………　13分

∴当时，△CPQ可能为直角三角形。　　　　　　　  …………　14分