《相交线、平行线》基础测试
(一)判断题(每小题2分,共10分)
1.把一个角的一边反向延长,则可得到这个角的邻补角……………………………( )
【提示】根据叙述,画出相应的图形即可判断.
【答案】√.
2.对顶角相等,但不互补;邻补角互补,但不相等…………………………………( )
【提示】两直线互相垂直时,对顶角相等且互补,邻补角互补且相等.
【答案】×.
3.如果直线a⊥b,且b⊥c,那么a⊥c……………………………………………( )
【提示】画图,a⊥b,则∠1=90°,b⊥c,则∠2=90°.
∴ ∠1=∠2.
∴ a∥c.
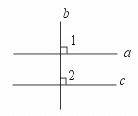
【答案】×.
【点评】由此题可知平面内垂直于同一直线的两直线互相平行,垂直关系没有传递性.
4.平面内两条不平行的线段必相交…………………………………………………( )
【提示】仔细读题,想想线段的特征,线段有两个端点,有一定的长度,它们可以延长后相交,但本身可以既不平行,也不相交.
【答案】×.
【点评】平面内两条不平行的线段可以相交,也可以不相交,但平面内两条不平行的线段的延长线一定相交.
5.命题有真命题、假命题,定理也有真定理假定理…………………………………( )
【提示】前一句话是对的,后一句话是错的.假命题不能成为定理,定理都是真命题.
【答案】×.
(二)填空题(每小题3分,共27分)
6.如图,直线AB、CD相交于点O,∠1=∠2.则∠1的对顶角是_____,∠4的邻补角是______.∠2的补角是_________.
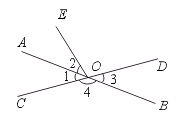
【提示】注意补角和邻补角的区别,前者只要求满足数量关系,即两角和为180°,而后者既要求满足数量关系又要求满足位置关系,即互补相邻.
【答案】∠1;∠1和∠3;∠BOE或∠4.
7.如图,直线AB和CD相交于点O,OE是∠DOB的平分线,若∠AOC=76°,则∠EOB=_______.
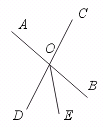
【提示】根据“对顶角相等”和“角平分线的定义”来求.
【答案】38°.
8.如图,OA⊥OB,OC⊥OD.若∠AOD=144°,则∠BOC=______.
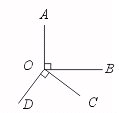
【提示】由OA⊥OB,OC⊥OD,可得∠AOB=∠COD=90°,一周角为360°.
【答案】36°.
9.如图,∠1的内错角是,它们是直线、被直线所截得的.
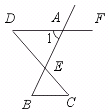
【答案】∠AEC和∠B,DF、DC(DF、BC)、AB.
10.如图,AB∥CD、AF分别交AB、CD于A、C.CE平分∠DCF,∠1=100°,则∠2= .
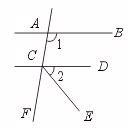
【提示】先证∠DCF=∠1=100°,再用“角平分线家义”来求∠2.
【答案】50°.
11.如图,∠1=82°,∠2=98°,∠3=80°,则∠4= .
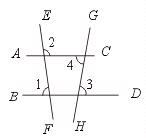
【提示】先判定AC∥BD.再利用平行线的性质求∠4的度数.
【答案】80°.
12.如图,直线AB∥CD∥EF,则∠a+∠b-∠g= .
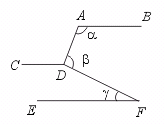
【提示】∵ AB∥CD,
∴ ∠ADC=∠a.
∵ ∠ACD+∠CDF+∠b=360°,
∴ ∠a+∠b +∠CDF=360°.
∴ ∠a+∠b =360°-∠CDF.
∵ CD∥EF,
∴ ∠CDF+∠g=180°.
∴ ∠a+∠b-∠g =360°-∠CDF-∠g =360°-(∠CDF+∠g).
∴ ∠a+∠b-∠g =180°.
【答案】180°.
13.“如果n是整数,那么2n是偶数”其中题设是 ,结论是 ,这是 命题(填真或假).
【提示】“如果”开始的部分是题设,“那么”开始的部分是结论.
【答案】n是整数,2n是偶数,真.
14.把命题“直角都相等”改写为“如果…,那么…”的形式是______________________.
【答案】如果几个角是直角,那么这几个角都相等.
(三)选择题(每题3分,共18分)
15.下列命题中,是真命题的是…………………………………………………………( )
(A)相等的两个角是对顶角.
(B)有公共顶点的两个角是对顶角.
(C)一条直线只有一条垂线.
(D)过直线外一点有且只有一条直线垂直于已知直线.
【答案】D.
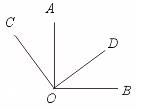
16.如图,OA⊥OB,OC⊥OD,垂足均为O.则∠BOC+∠AOD等于…………( )
(A)150° (B)160° (C)170° (D)180°
 【提示】延长BO到E.
【提示】延长BO到E.
∵ OA⊥OB,
∴ OA⊥OE.
又 OC⊥O(D)
∴ ∠AOC+∠COE=∠AOC+∠AOD=90°.
由同角的余角相等知:∠COE=∠AOD.
∴ ∠BOC+∠AOD=∠BOC+∠COE=180°.
【答案】D.
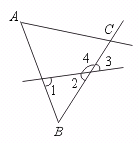
17.如图,下列判断:①∠A与∠1是同位角;②∠A与∠B是同旁内角;③∠4与∠1是内错角;④∠1与∠3是同位角.其中正确的是…………………………………( )
(A)①、②、③ (B)①、②、④ (C)②、③、④ (D)①、②、③、④
【提示】可将涉及的一对角从整个图形中分离出来,单独观察.如
①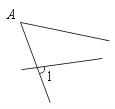 ②
②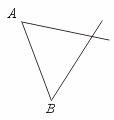 ③
③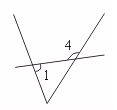 ④
④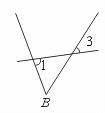 这样可排除图中其它线的干扰,便于确定两角的相对位置.易知①、②、③正确.
这样可排除图中其它线的干扰,便于确定两角的相对位置.易知①、②、③正确.
【答案】A.
18.如图,图中的同位角共有……………………………………………………………( )
(A)6对 (B)8对 (C)10对 (D)12对
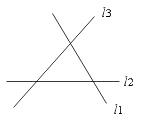
【提示】可采用17题的方法.
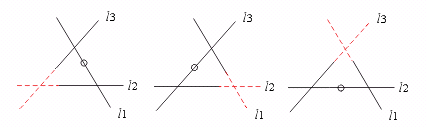
两条直线被第三条直线所截,同位角有四对,图中有三组两条直线被第三条直线所截,均共有同位角4×3=12对.
【答案】D.
19.如图,下列推理正确的是…………………………………………………………( )
(A)∵ ∠1=∠2,∴ AD∥BC (B)∵ ∠3=∠4,∴ AB∥CD
(C)∵ ∠3=∠5,∴ AB∥DC (D)∵ ∠3=∠5,∴ AD∥BC
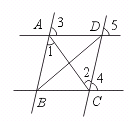
【答案】C.
20.如图,AB∥CD.若∠2是∠1的两倍,则∠2等于……………………………( )
(A)60° (B)90° (C)120° (D)150°
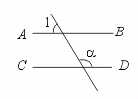
【提示】由AB∥CD,可得∠3+∠2=180°.
∵ ∠1=∠3,
∴ ∠1+∠2=180°.
∵ ∠2=2∠1,
∴ 3∠1=180°.
∴ ∠1=60°.
∴ ∠2=2×60°=120°.
【答案】D.
(四)画图(本题6分)
21.如图,分别作出线段AB、BC、的垂直平分线,设交点为O,连结OA、OB、OC.量得OA=( )mm,OB=( )mm,OC=( )mm.则OA、OB、OC的关系是.
【答案】18,18,18.OA=OB=OC.
(五)完成下列推理,并填写理由(每小题8分,共16分)
22.如图,∵ ∠ACE=∠D(已知),
∴ ∥ ( ).
∴ ∠ACE=∠FEC(已知),
∴ ∥ ( ).
∵ ∠AEC=∠BOC(已知),
∴ ∥ ( ).
∵ ∠BFD+∠FOC=180°(已知),
∴ ∥ ( ).
【答案】CE,DF,同位角相等,两直线平行;
EF,AD,内错角相等,两直线平行;
AE、BF,同位角相等,两直线平行;
EC,DF,同旁内角互补,两直线平行.
23.如图,∠B=∠D,∠1=∠2.求证:AB∥CD.
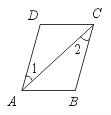
【证明】∵ ∠1=∠2(已知),
∴ ∥ ( ),
∴ ∠DAB+∠ =180°( ).
∵ ∠B=∠D(已知),
∴ ∠DAB+∠ =180°( ),
∴ AB∥CD( ).
【答案】AD,BC,内错角相等两直线平行;
B,两直线平行,同旁内角互补;
D,等量代换,
同旁内角互补,两直线平行.
(六)计算或证明(第24、25、26每小题6分,第27题5分,共23分)
24.如图,a∥b,c∥d,∠1=113°,求∠2、∠3的度数.
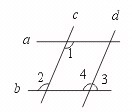
【提示】由a∥b,∠1=113°,可求∠2.由c∥d和求出的∠2的度数可求∠4.然而求出∠3.
【答案】∠2=113°.∠3=67°.
∵ a∥b(已知).
∴ ∠2=∠1=113°(两直线平行,内错角相等).
∵ c∥d(已知).
∴ ∠4=∠2=113°(两直线平行,同位角相等).
∵ ∠3+∠4=180°(邻补角定义),
∴ ∠3=67°(等式性质).
25.已知:如图,AD∥EF,∠1=∠2.求证:AB∥DG.

【提示】证明∠BAD=∠2.
【证明】∵ AD∥EF(已知),
∴ ∠1=∠BAD(两直线平行,同位角相等).
∵ ∠1=∠2(已知),
∴ ∠BAD=∠2(等量代换).
∴ AB∥DG(内错角相等,两直线平行).
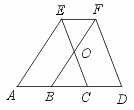
26.已知:如图,D是BC上的一点.DE∥AC,DF∥AB.
求证:∠A+∠B+∠C=180°.
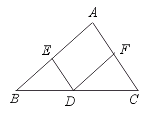
【提示】由DE∥AC,DF∥AB,先证:∠A=∠EDF,再证∠A+∠B+∠C=180°.
【证明】∵ DE∥AC(已知),
∴ ∠BED=∠A,∠BDE=∠C(两直线平行,同位角相等).
∵ DF∥AB(已知),
∴ ∠BED=∠EDF(两直线平行,内错角相等),
∠FDC=∠B(两直线平行,同位角相等).
∴ ∠EDF=∠A(等量代换).
∵ ∠BDE+∠EDF+∠FDC=180°(平角定义),
∴ ∠C+∠A+∠B=180°(等量代换).
即 ∠A+∠B+∠C=180°.
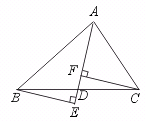
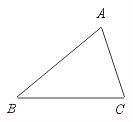
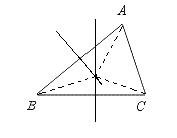
27.如图,如果D是BC的中点,那么B、C两点到直线AD的距离相等.试写出已知,求证,并补全图形(不证明).
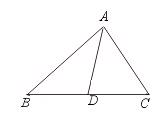
【提示】B、C两点的直线AD的距离,是点到直线的距离.即相应的“垂线段”的长度.可用三角尺画出图形.
【答案】图形如图所示,
已知:BD=CD,且BE⊥AD,CF⊥AD,垂足分别为E、F.
求证:BE=CF.