中考数学模拟试题（四）

班级：_________　姓名：_________　得分：_________

一、填空题(每小题3分，共30分)

1．计算：(sin30°)·(tan60°)-1＝______．

2．第一宇宙速度约为7919.米/秒，将它保留两个有效数字后的近似数是______．

3．已知点P(a，a-2)在第四象限，则a的取值范围是______．

4．等腰直角三角形斜边长为，则它的面积为______．

5．已知梯形的中位线的长是9，一条底边的长是12，那么另一条底边的长是______．

6．若一组数据6，7，5，6，x，1的平均数是5，则这组数据的众数是______．

7．如图1是一个矩形的窗框，中间被两等宽的木条分成四个小矩形，其中三个小矩形的面积分别为0.4平方米、0.2平方米、0.55平方米，则第四个小矩形(图中阴影部分)的面积为______平方米．

　　

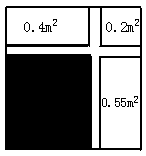
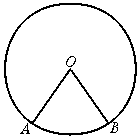
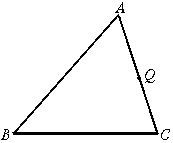
图1　　　　　　　  图2　　　　　　　　　　　  图3

8．当0≤x＜1时，化简＋1＋x-1的结果是______．

9．已知k≠0，则函数①y＝kx＋b(b是常数)，②y＝，③y＝kx²中，图象不一定经过原点的是______．(填写序号)

10．如图2，A、B是⊙O上两点，且∠AOB＝70°，若C是⊙O上不与A、B重合的一个动点，则∠ACB的度数是______．

二、选择题(每小题3分，共18分)

11．计算2sin30°-2cos60°＋tan45°的结果是(　)

　　A．2　　　　　　　　　　　　　　B．　　C．　　　　　　　　　　　　　　　　　D．1

12．用配方法解一元二次方程x²-2x-m＝0，配方后得到的方程应该是(　)

　　A．(x-1)²＝m²＋1　　B．(x-1)²＝m-1　　C．(x-1)²＝1-m　　D．(x-1)²＝m＋1

13．如图3，已知点Q是△ABC边AC上的一点，过点Q作直线l交AB于 点P，使截得的△APQ与△ABC相似，则这样的直线l可以作出(　)

　　A．1条　　　　　　　　　　　　　　　B．2条　　C．3条　　　　　　　　　 D．4条

14．已知一个函数满足下表(x为自变量)，则y与x之间的函数关系式为(　)

x	…	-3	-2	-1	1	2	3	…
y	…	1	1.5	3	-3	-1.5	-1	…

　　A．y＝　　　　　　　　　　 B．y＝-　　C．y＝-　　　　　　　　　　　　D．y＝

15．假定甲、乙两人在一次赛跑中，路程s与时间t的关系如图4所示，那么下面说法正确的是(　)

　　　A．甲比乙先出发;　　B．乙比甲跑的路程多

　　C．甲、乙两人的速度相同;  D．甲先到达终点

16．在△ABC中，BC＝3，内切圆的半径为r＝，则cot＋cot的值是(　)

　　　A．2　　　　　　　　　　　　 B．　　C．　　　　　　　　　　　　D．

三、解答题(17～18每小题6分，19～23每小题8分，共52分)

17．化简：÷．

18．关于x的一元二次方程(2m-1)x²-4mx＋m＋3＝0的两个实数根绝对值相等，求m的值．

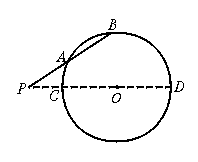
19．某机械传动装置在静止状态时，如图5所示，连杆PB与点B运动所形成的⊙O交于点A，现测得PA＝4 cm，AB＝5 cm，⊙O的半径R＝4.5 cm，求点P到圆心O的距离．

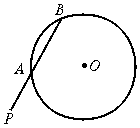
　　　　　　　　　　　　　　　　　　　　　　　　　　　　  图5

20．某商店积压了100件某种商品，为使这批货物尽快脱手，该商店采取了如下销售方案，先将价格提高到原来的2.5倍，再作三次降价处理：第一次降价30%，标出“亏本价”；第二次降价30%，标出“破产价”；第三次降价30%，标出“跳楼价”三次降价处理销售结果如下表：

降价次数	一	二	三
销售件数	10	40	一抢而光

　　问：(1)跳楼价占原价的百分比是多少？

　　(2)该商品按新销售方案销售，相比原价全部售完，哪一种方案更盈利？

　　21．已知：如图6中，P为等边△ABC的外接圆BC弧上的一点，AP交BC于E，

　　求证：(1)AB²＝PA·AE； (2)PA²＝AB²＋PB·PC．

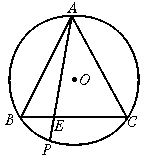
　　　　　　　　　　　　　　　　　　　　　　　　 　　　　　图6

22．某广告公司设计一幅周长为12米的矩形广告牌，广告设计费为每平方米1000元．设矩形一边为x米，面积为S平方米．

　　(1)求出S与x之间的函数关系式，并确定自变量x的取值范围；

　　(2)请你设计一个方案，使获得的设计费最多，并求出这个费用；

　　(3)为使广告牌美观、大方，要求做成黄金矩形，请你按要求设计，并计算出可获得的设计费约是多少元(精确到元)

　　(参考资料：若矩形的长为a，宽为b，且满足a²＝b(a＋b)，则称这样的矩形为黄金矩形;≈2.2))

23．如图7，O为圆柱形木块底面的圆心，过底面的一条弦AD，沿母线AB剖开，得剖面矩形ABCD，AD＝24 cm，AB＝25 cm．若的长为底面周长的，如图8所示．

　　(1)求⊙O的半径；

　　(2)求这个圆柱形木块的表面积．(结果可保留p 和根号)

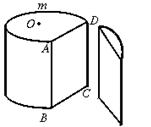
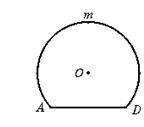
　　　　　　　　　　　　　　　　　　 图7　　　　　　　　　　　　 图8

参考答案

一、1．　2．7.9×10³米/秒　3．0＜a＜2　4．　5．6　

6．5和6　7．1.1　8．2　9．②　10．35°或145°

二、11．D　12．D　13．B　14．B　15．D　16．A

三、17．

18．由a＝2m-1≠0，∴　m≠　　　　　　　　　 ①

　　Δ＝16m²-4(2m-1)(m＋3)＝8m²-20m＋12≥0，

　　∴　1≥m或m≥　　　　　　　　　　　　　　　　　　　　 ②

　　∵　x₁＝x₂，分两种情况：

(1)若两根同号，则x₁＝x₂，

∴　Δ＝0，得m₁＝1，m₂＝　　　　　　　　 ③

　　(2)若两根异号，则x₁＋x₂＝0，x₁·x₂＜0，

　　即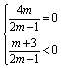

　　∴　m＝0　　　　　　　　　　④

　　由①②③④得：m＝0，1，

19．解：连结PO并延长，交⊙O于C、D，则有PA·PB＝PC·PD，

　　∵　PC＝OP-R＝OP-4.5，PD＝OP＋R＝OP＋4.5，

　　从而有(OP-4.5)(OP＋4.5)＝4(4＋5)，

　　∴　OP²＝36＋20.25＝56.25．又∵　OP＞0∴　OP＝7.5( cm)．

　　∴　点P到圆心O的距离为7.5 cm．

20．(1)设原价为x，则跳楼价为2.5x(0.7×0.7×0.7)

所以跳楼价占原价的百分比为＝85.75%．

(2)按原价出售的销售金额为100x，按新价出售的销售金额为

2.5x×0.7×10＋2.5x×0.7×0.7×40＋2.5x×0.7³×50＝109.375x．

　　因为109.375x＞100x，所以新方案销售更盈利．

21．(1)连结BP，则∠P＝∠C．

又因为△ABC等边，所以∠ABC＝∠C＝∠P．

　　又因为∠BAP＝∠BAP，所以△ABE∽△APB，

　　∴　

　　∴　AB²＝PA·AE

　　(2)连结PC，可证：△APC∽△BPE．

22．解：(1)设矩形的另一边长为y，则由2x＋2y＝12，得y＝6-x，

　　∴　S＝xy＝x(6-x)＝-x²＋6x ，(0＜x＜6)．

　　(2)S＝-x²＋6x＝-(x-3)²＋9，

　　∵　当x＝3时，S的最大值为9，

　　此时可获得最多设计费为：9×1000＝9000(元)．

　　(3)设计此矩形的长为x米，宽为y米，则有解得

　　(x＝-3-3不合题意，舍去)

　　∴　当矩形的长为x＝3-3时，此矩形为黄金矩形．

　　此时S＝xy＝(3-3)(9-3)＝36(-2)，

　　∴　可获得设计费为：36(-2)1000＝7200(元)．

23．(1)连结OA、OD作OE⊥AD于E，易知∠AOD＝120°，AE＝12 cm，

可得AO＝r＝＝8cm．

　　(2)圆柱形表面积2S_圆＋S_侧＝(384p  ＋400p  ) cm²．