中考数学模拟试题一
班级_____________ 姓名____________
一、选择题（每题3分，共30分）
1、若（x－1）0 ＝1，则( )
A．x≥1 ； B．x≤1； C．x≠1； D．x为任意实数
2、将一组数据中的每一个数据的值都减去同一个常数，那么下列结论正确的是（ ）
A．平均数； B．方差不变； C．方差改变； D．方差改变，但标准差不变
3、若函数
是正比例函数，则m的值为（ ）
A．
； B．
； C．3； D．－3
4、某商品原价为a元，因需求量大，经营者两次提价，每次提价10%，后因市场物价调整 ，又一次降价20%，降价后这种商品的价格是（ ）
A．0.968a元； B．0.88a元； C．1.08a元； D．a元
5、已知矩形对角线长是5cm，那么顺次连结矩形四边中点所得的四边形的周长为（ ）
A．20cm； B．5cm； C．2.5cm； D．10cm
6、某村去年粮食总产量为m吨（m为常数），设该村粮食的人均产量为y 吨，人口数为x ,则y与x 之间的函数关系的大致图像为（ ）
7、ΔABC为⊙O的内接三角形，且∠C=90°，CD⊥AB于D，若AD＝8,BD＝4，则tgA＝( )
A．
； B．
； C．
； D．
8、已知RtΔABC 中，C ＝90°，斜边长为5，两直角边的长分别是方程x2－(2m－1)x＋4(m－1)＝0的根，则m的值等于（ ）
A．－1； B．4； C．－4或1； D．－1或4
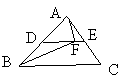
9、如图，DE是ABC的中位线，ABC的平分线交DE于点F，
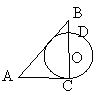连结AF，若∠ABC＝50°，则∠AFD＝（ ）
A．45°； B．55°； C．65°； D．75°
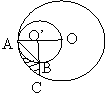
10、 如图，在RtΔABC中，∠C＝90°，AC＝4，BC＝3，以
BC上一点O为圆心作⊙O与AC、AB都相切，与BC的交点
为D，则BD＝（ ）
A．1； B．
； C．
； D．
二、填空：（每题3分，共24分）
11、计算：
______________
12、因式分解：
＝____________________________
13、ΔABC中，若∠A＝55°，∠B＝35°，则sin2A＋sin2B＝______________
14、若（2，5），（4，5）是抛物线y＝ax2＋bx＋c上的两点，那么它的对称轴是____________
15、若方程组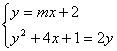
没有实数解，则实数m的取值范围是_________________
16 、已知1＋3＝4＝22，1＋3＋5＝9＝32，1＋3＋5＋7＝16＝42，1＋3＋5＋7＋9＝25＝52，…，试根据前面各式的规律，猜测出1＋＋5＋7＋9＋…＋（2n＋1）＝________________________（其中n 为正整数）
17、已知如图所示，OA为⊙O的半径，AB是以OA为直径的⊙O’
的弦，O’B的延长线交⊙O于点C，且OA＝4，∠OAB＝45°，
则图中阴影部分的面积为________________
18、如图，矩形ABCD中，AB＝2，BC＝1，E是DC上一点，
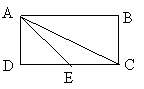∠DAE＝∠BAC，则EC的长为_________________
三、解答题
19、解方程：
；
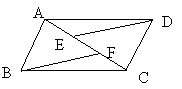
20、如图，已知平行四边形ABCD中，E、F为AC上两点，且DE∥BF，求证：AE＝CF
 |
21、已知一次函数y＝4x＋8与反比例函数y＝
只有 一个交点，求k的值及交点坐标。
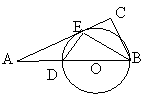
22、如图在ΔABC中，∠C＝90°，BE是ΔABC的角平分线，DE⊥BE交AB于D，O是ΔBDE的外接圆，（1）求证：AC是O的切线；（2）若AD＝6，AE＝6，求DE的长。
 |
23、用大小两种箱子包装720件产品，有三种包装方案：
方案一：产品的一半用大箱装，一半用小箱装；
方案二：产品的
用大箱装，其余用小箱装；
方案三：产品的
用大箱装，其余用小箱装，那么比“方案一”可少用5只箱子。
如果每只大箱子的包装费比每只小箱子的包装费高k%，试确定选择哪种包装方案能使包装费用最低？
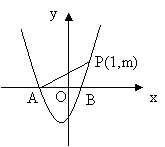
24、如图，二次函数y＝x2＋bx＋c的图像与x 轴交于A、B两点，点A在原点的左边，点B在原点右边防军，点P（1，m）在抛物线上，AB ＝2，tg∠PAO ＝
；
（１）求m的值；
（２）求二次函数的解析式；
（３）
在x 轴的下方是否存在一点D，使ΔDAO的面积等于ΔPAO的面积？若存在，求出D点坐标，若不存在，请说明理由。
25、如图在矩形ABCD中，E为AD的中点，EF⊥EC交AB于F，连结FC。
（１）求证：ΔAEF∽ΔECF；
（２）若F为AB上一动点，设AF＝x，SΔEFC＝y，求y关于x 的函数关系式，并写出函数的定义域；
（３）
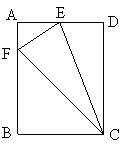若BC＝2，CD＝3，求当F运动到什么位置时，ΔCEF为等腰三角形。