中考数学填空百题训练
1. 点P(1，2)关于y轴对称的点的坐标是 ．
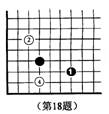
2. 如图所示，直线a∥b，则∠A= 度．
3. 已知⊙O的半径为8, 圆心O到直线l的距离是6, 则直线l与⊙O的位置关系是 ．
4.
如果直角三角形的斜边与一条直角边的长分别是13cm和5cm，那么这个直角三角形的面积
是 cm2．
5.当
时,分式
的值为零.
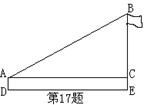
6.如图的围棋盘放在某个平面直角坐标系内,白棋② 的坐标为
,白棋④的坐标为
,那么黑棋①的坐标应该是
.
7.学校食堂出售两种厚度一样但大小不同的面饼,小饼直径
,售价30分;大饼直径
,售价40分.你更愿意买
饼,原因是
.
8．计算：1－3=________。
9．有一个密码系统，其原理由下面的框图所示： 输入x → x+6 → 输出 当输出为10时，则输入的x=________。
10．已知两圆的半径分别为4厘米和1厘米，若两圆外切，则两圆的圆心距为________厘米。
11．当x>2时，化简
=________。
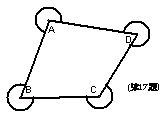
12．初三（1）班研究性学习小组为了测量学校旗杆的高度（如图），他们离旗杆底部E点30米的D处，用测角仪测得旗杆的仰角为30º，已知测角仪器高AD=1.4米，则旗杆BE的高为________米（精确到0.1米）。
13．计算：
=_______________
14．分解因式：
=______________________
15．已知a，b，c，d是成比例线段，其中a=3cm，b=2cm，c=6cn，则d=_______cm
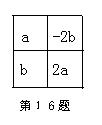
16．如图，沿正方形的对角线对折，把对折后重合的两个小正方形内的单项式相乘，乘积 是___________。（只要写出一个结论）
17．如图，ABCD是各边长都大于2的四边形，分别以它的顶点为圆心、1为半径画弧（弧的端点分别在四边形的相邻两边上），则这4条弧长的和是________________
|
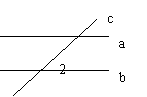
１8、如图，直线a,b被直线c所截，a∥b如果∠1=50°， 那么∠2=____度。
１9、冬季的某一天，我市的最高气温为7℃，最低气温为-2℃，那么这天我市的最高气温比最低气温高___℃。
20、请写出一个图象经过点（１，４）的函数解析式：________.
21、一只袋内装有2个红球、3个白球、5个黄球（这些球除颜色外没有其它区别），从中任意取出一球，则取得红球的概率是_____________
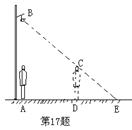22、如图，小明从路灯下，向前走了5米，发现自己在地面上的影子长DE是2米，如果小明的身高为1.6米，那么路灯离地面的高度AB是_________米。
23．已知
，则
=
．
24．当
≥0时，化简：
=
．
25．因式分解：
3－=
.分解因式2x2－18 = .
26．在平行四边形、矩形、菱形、正方形、等腰梯形的五种图形中，既是轴对称、又是中心对称的图形是 ．
27．下列是三种化合物的结构式及分子式，请按其规律，写出后一种化合物的分子式
．
25.已知抛物线解析式为y=x2－3,则此抛物线的顶点坐标为 .
26.已知一个底面直径为10cm,母线长为8cm的圆锥形漏斗,它的侧面积是 cm.
27.在航天知识竞赛中包括甲同学在内的6名同学的平均分为74分,其中甲同学考了89分,则除甲以外的5名同学的平均分为 分.
28.实数a在数轴上的位置如图所示,化简
= .
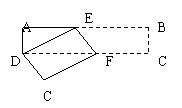28.矩形纸片ABCD中,AD=4cm ,AB=10cm,按如图方式折叠,使点B与点D重合,折痕为EF,则DE=
cm.
29．在等式
的两个方格内分别填入一个数，使这两个数是互为相反数且等式成立。则第一个方格内的数是___________
30．在中考体育达标跳绳项目测试中，1分钟跳160次为达标，小敏记录了他预测时1分钟跳的次数分别为145,155,140,162,164，则他在该次预测中达标的概率是__________
32．平移抛物线
，使它经过原点，写出平移后抛物线的一个解析式____________________
33．实验中学初三年级12个班中共有团圆a人，则
表示的实际意义是________________________________
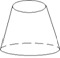
34下列空间图形中是圆柱的为
（A）
（B）
（C）
（D）
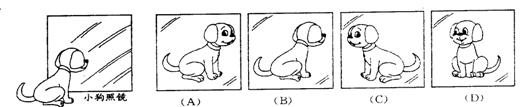
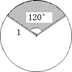
35、一只小狗正在平面镜前欣赏自己的全身像（如图所示），此时，它所看到的全身像是
 |
36．如图，半径为1的圆中，圆心角为120°的扇形面积为
37．关于
的一元二次方程
，实数根的情况是
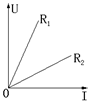38．阻值为
和
的两个电阻，其两端电压
关于电流强度
的函数图象如图，则阻值
。
39．不等式组
的解集在数轴上可以表示为（ ）
|
（A） （B） （C） （D）
40．某超市进了一批商品，每件进价为a元，若要获利25%，则每件商品的零售价应定为 （用含的代数式表示）
41．如图，在这三张扑克牌中任意抽取一张，抽到“红桃7”的概率是 .
42．试写出图象位于第二象限与第四象限的一个反比例函数解析式 .
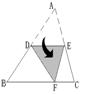43．如图，D、E为△ABC两边AB、AC的中点，将△ABC沿线段DE折叠，
使点A落在点F处，若∠B=55°，则∠BDF= °.
44．某种药品的说明书上，贴有如右所 示的标签，一次服用这种药品的剂
量范围是 
～ .
45．小舒家的水表如图所示，该水表的读数
为
（精确到0.1）.
46．在计算器上按照下面的程序进行操作：
| x | -2 | -1 | 0 | 1 | 2 | 3 |
| y | -5 | -2 | 1 | 4 | 7 | 10 |
下表中的x与y分别是输入的6个数及相应的计算结果：
上面操作程序中所按的第三个键和第四个键应是
.
47、计算：2xy＋3xy＝_________。
48、已知反比例函数y＝的图象经过点(1，2)，则k的值是_________。
49、在实数范围内分解因式：ab2－2a＝_________.
50、若二次函数y＝x2－4x＋c的图象与x轴没有交点，其中c为整数，则c＝_________.(只要求写出一个)
51．点P(-1, 3 )关于原点对称的点的坐标是 .
52．抛物线y= ( x – 1)2 – 7的对称轴是直线 ..
53．有一面积为60的梯形,其上底长是下底的1/3,若下底的长为x,高为y,则y与x的函数关系式为 .
54.某种商品原价50元.因销售不畅,3月份降价10%,从4月份开始涨价,5月份的售价为64.8元,则4、5月份两个月平均涨价率为 .
55.掷一颗普通的正方形骰子,点数为偶数的概率为 .
56、现有7名同学测得某大厦的高度如下：（单位：
）29.8
30.0 30.0 30.0 30.2 44.0 30.0 。(1) 在这组数据中,中位数是
， 众数是 ，平均数是
；
(2) 凭经验，你觉得此大厦大概有多高?请简要说明理由.
57．
在两个连续整数a和b之间，a<<b, 那么a , b 的值分别是
。
58．如果两个相似三角形对应高的比是1：2，那么它们的面积比是 。
59某商店出售下列形状的地板砖：①正三角形；②正方形；③正五边形；④正六边形.如果只限于用一种地板砖镶嵌地面，那么不能选购的地板砖序号是________．
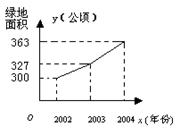
60．近年来市政府不断加大对城市绿化的经济投入，使全市绿地面积不断增加．从2002年底到2004年底城市绿地面积变化如图所示，那么绿地面积的年平均增长率是__________．
61、计算：(a-b)2-(a+b)2=
62、A(2，4)在正比例函数的图象上，这个正比例函数的解析式是
63．锐角Ａ满足２ｓｉｎ(Ａ－１５０)＝
则∠Ａ＝＿＿＿＿
64．工程上常用钢珠来测量零件上小孔的直径。假设钢珠的直径是１２毫米，测得
钢珠顶端离零件表面的距离为９毫米，如图６所示，则这个小孔的直径ＡＢ是＿＿＿＿毫米
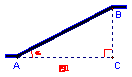
65．如图，自动扶梯AB段的长度为20米，倾斜角A为α，高度BC为 米(结果用含α的三角比表示).
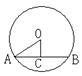
66、如图3，⊙O的半径是5cm，圆心到弦AB的距离为3cm，则弦AB的长是＿＿＿。
67．如图是由一些相同的小正方体构成的几何体的三视图，这些相同的小正方体的个数有 个．
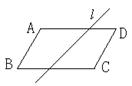
68. 已知任意直线l把□ABCD分成两部分，要使这两部分的面积相等，直线l所在位置需满足的条件是 _________ (只需填上一个你认为合适的条件)
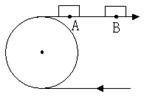
69. 如图，某传送带的一个转动轮的半径为20cm，当物体从A传送20cm
至B时，那么这个转动轮转了 _________ 度(π取3.14，结果保留四个有效数字).
70、甲、乙两个同学在几次测验中，平均分都是86分，甲的方差是0.61，乙的方差是0.72，则可知成绩较稳定情况是＿＿＿＿（填甲或乙或一样）稳定。
71、小华要从长度分别为5cm，6cm，11cm，16cm的四根小木棒中选出三根摆成一个三角形，那么他选的三根木棒的长度分别是 。
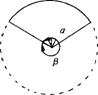
72．如图，扇子的圆心角为α，余下扇形的圆心角为β，为了使扇子的外形美观，通常情况下α与β的比按黄金比例设计，若取黄金比为0．6，则α= 度．
|
|
|
73.将一张长方形的纸对折,如图所示,可得到一条折痕(图中虚线),继续对折,对折时每次折痕与上次的折痕保持平行,连续对折三次后,可以得到7条折痕,那么对折四次可以得到 条折痕,如果对折n次,可以得到 条折痕.
74. 在日常生活中如取款、上网等都需要密码．有一种用“因式分解”法产生的密码，方便记忆．原理是：如对于多项式
，因式分解的结果是
，若取x=9，y=9时，则各个因式的值是：(x－y)=0，(x+y)=18，(x2+y2)=162，于是就可以把“018162”作为一个六位数的密码．对于多项式
，取x=10，y=10时，用上述方法产生的密码是： (写出一个即可)．
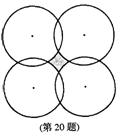
75.四个半径均为
的圆如图放置,相邻两圆交点之间的距离也等于,不相邻两圆圆周上两点间的最短距离等于2,则等于 ,图中阴影部分面积等于
.(精确到0.01)
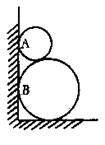
76．如图，两圆轮叠靠在墙边，已知两轮半径分别为4和1，则它们与墙的切点A，B间的距离为________________________
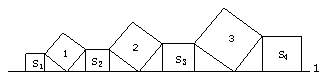
77、在直线l上依次摆放着七个正方形(如图所示)。已知斜放置的三个正方形的面积分别是1、2、3，正放置的四个正方形的面积依次是S1、S2、S3、S4，则S1＋S2＋S3＋S4＝_______。
78、杉杉打火机厂生产某种型号的打火机，每只的成本为2元，毛利率为25%。工厂通过改进工艺，降低了成本，在售价不变的情况下，毛利率增加了15%，则这种打火机每只的成本降低了_________元.(精确到0.01元。毛利率＝)
79.计算：
-
；
80、 解方程：
．
81、－2－(
－1)0+
82计算：2(x＋1)－x．
83、
84、计算：