中考模拟考试数学试卷（1）

题号	一	二	三	总分
得分

一、填空题 (本大题共6小题，每小题3分，共18分)

1．=　　　　 ．

2．函数y=的自变量取值范围是　　　　 ．

3．观察下列各式：×2=+2，×3=+3，×4=+4，×5=+5…想一想，什么样的两数之积等于这两数之和？设n表示正整数，用关于n的等式表示这个规律为　　　　　　　　　　　 ．

4．如果反比例函数y=的图象经过点P（-3，1）那么k=　　　　 ．

5．如果一个角的补角是120°，那么这个角的余角是　　　　 ．

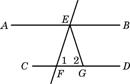
6．如图：AB∥CD，直线EF分别交AB、CD于E、F，EG平分∠BEF，若∠1=72°,则∠1=72°,则∠2=　　　　 ．

二、选择题（本大题共8个小题，每小题4分，满分32分）

7．下列计算正确的是（　　）

A．（-4x²）(2x²+3x-1)=-8x⁴-12x²-4x　　　　　　　　　　　　　　　　 B．(x+y)(x²+y²)=x³+y³

C．(-4a-1)(4a-1)=1-16a²　　　　　　　　　　　　　　　　　　　　　　　　D．(x-2y)²=x²-2xy+4y²

8．把x²-1+2xy+y²的分解因式的结果是（　　）

A．（x+1）(x-1)+y(2x+y)　　　　　　　　　　　　　　　　　　　　　　　　 B．(x+y+1)(x-y-1)

C．(x-y+1)(x-y-1)　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　D．(x+y+1)(x+y-1)

9．已知关于x的方程x²-2x+k=0有实数根，则k的取值范围是（　　）

A．k＜1　　　　　　 B．k≤1　　　　　　　　　　 C．k≤-1　　　　　　　　　 D．k≥1

10．某电视台举办的通俗歌曲比赛上，六位评委给1号选手的评分如下：90　96 91 96 95　94这组数据的众数和中位数分别是（　　）

A．94.5，95　　　 B．95，95　　　　　　　　 C．96，94.5　　　　　　　D．2，96

11．面积为2的△ABC，一边长为x，这边上的高为y，则y与x的变化规律用图象表示大致是（　　）

A　　　　　　　 B　　　　　　　　 C　　　　　　　 D

12．有如下结论（1）有两边及一角对应相等的两个三角形全等；（2）菱形既是轴对称图形又是中心对称图形；（3）对角线相等的四边形是矩形；（4）平分弦的直径垂直于弦，并且平分弦所对的两条弧；（5）两圆的公切线最多有4条，其中正确结论的个数为（　　）

A．1个　　　　　　　B．2个　　　　　　　　　　　C．3个　　　　　　　　　　 D．4个

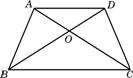
13．已知：如图梯形ABCD中，AD∥BC，AB=DC，AC与BD相交于点O，那么图中全等三角形共有（　　）对.

A．1对　　　　　　　B．2对　　　　　　　　　　　C．3对　　　　　　　　　　 D．4对

　　　　　　　　

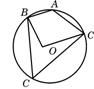
14．如图四边形ABCD内接于⊙O，若∠BOD=100°，则∠DAB=（　　）

A．50°　　　　　　 B．80°　　　　　　　　　　 C．100°　　　　　　　　　 D．130°

三、解答题（本大题共7个小题，共70分）

15．（本小题6分）计算：+-4

16．（本小题7分）解方程： -8x²+12=0

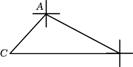17．（6分）某中学团委到位于A市南偏东60°方向50海里的B基地慰问驻车，然后乘船前往位于B基地正西方向的C哨所看望值班战士，C哨所位于A市的南偏西43°方向，求C到A的距离（精确到1海里，以下数据供选用sin43°≈0.68,cos43°≈0.73）

18．（4分）平原上有A、B、C、D四个村庄，为解决当地缺水问题，政府准备投资修建一个蓄水池，不考虑其它因素，请你画图确定蓄水池H点的位置，使它与四个村庄的距离之和最小.（不作证明）

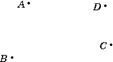
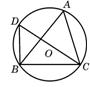
19．（本小题5分）阅读材料，解答问题：

如图，在锐角△ABC中，BC=a,CA=b,AB=c,△ABC的外接圆的半径为R，则===2R

证明：连结CO并延长交⊙O的直径，∴∠DBC=90°,

在Rt△DBC中，

∵sin D==,

∴sin A=sin D=　∴=2R

同理=2R,=2R

前面的阅读材料中略去=2R,=2R的证明过程，请你把B =2R的证明过程补写出来.

20．（12分）某图书馆开展两种方式的租书业务，一种是使用会员卡，另一种是使用租书卡，使用这两种卡租书，租书金额y（元）与租书时间x(天)之间的关系如下图所示.

（1）分别求出用租书卡和会员卡租书的金额y（元）与租书时间x（天）之间的函数关系式.

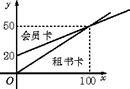（2）两种租书方式每天租书的收费分别是多少元？（x≤100）

21．（8分）某校师生去外地参加夏令营活动，车站提出两种车票价格的优惠方案供学校选择.第一种方案是教师按原价付款，学生按原价的78%付款；第二种方案是师生都按原价的80%付款；该校有5名教师参加这项活动，试根据夏令营的学生人数选择购票付款的最佳方案？

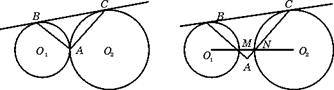
22．（8分）初三（几何）课本中有这样的一道习题，若⊙O₁与⊙O₂外切于点A，BC是两圆的一条外公切线，B、C为切点，则AB⊥AC

（1）若⊙O₁和⊙O₂外离，BC为两圆的外公切线，B，C为切点，连心线O₁O₂分别交⊙O₁，⊙O₂于M，N，设BM与CN的延长线交于A，试问AB与AC是否垂直？证明你的结论.

（2）若⊙O₁与⊙O₂相交，AB与AC垂直吗？

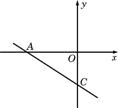
23．（14分）函数y=-x-12的图象分别交x轴，y轴于A,C两点，

（1）求出A、C两点的坐标.

（2）在x轴上找出点B，使△ACB~△AOC，若抛物线经过A、B、C三点，求出抛物线的解析式.

（3）在（2）的条件下，设动点P、Q分别从A、B两点同时出发，以相同的速度沿AC、BA向C、A运动，连结PQ，设AP=m，是否存在m值，使以A、P、Q为顶点的三角形与△ABC相似，若存在，求出所有的m值；若不存在，请说明理由.

2007年山西省中考模拟考试数学试卷（一）参考答案

一、1．　 2．x≥2　 3．(n+1)=+(n+1)　4．-3　5．30°　　6．54°

二、7．C　8．D　9．B　10．C　11．C　12．B　13．C　14．D

三、15．解：原式=3+3-2···················································· 4分

=3······································································· 6分

16．解：设2x²-3=y,则原方程变形为-4y=0·································· 1分

整理得1-4y²=0

解这个方程得，y₁=,y₂=-························································· 3分

当y₁=时，2x²-3=，解得：x=±········································ 4分

当y₂=-时，2x²-3=-，解得：x=±····································· 5分

经检验知，它们都是原方程的根.

所以原方程的根是：x=±，x=±······································ 7分

17．解：过A作AD⊥BC于D，···················································· 1分

在Rt△ADB中，∠DAB=60°,AB=50海里，AD=AB cos 60°=25(海里)　

····································································································· 3分

在Rt△ADC中，cos43°=，AC=≈34（海里）·············· 5分

答：C到A的距离约是34海里.

18．作法：连结AC与BD交点为H点，则H点即为所求的点.········ 4分

19．连结BO并延长交⊙O于E，连结EA，则∠ACB=∠E··············· 1分

∵BE是⊙O的直径，

∴∠BAE=90°················································································ 2分

在Rt△ABE中，sinE==····················································· 3分

∴sin∠ACB=sinE=···································································· 4分

∴=2R·············································································· 5分

20．解：（1）租书卡：设y=kx························································· 1分

观察图象知，当x=100时，y=50，

∴100k=50，解得k=　 ∴y=x·················································· 3分

用会员卡时，设y=kx+b··································································· 4分

∵(0,20),(100,50)在直线y=kx+b上，

∴····································· 6分

∴y=x+20

（2）用租书卡的方式租书，每天租书的收费为50÷100=0.5（元）··· 9分

用会员卡的方式租书，每天租书的收费为（50-20）÷100=0.3（元）

······································································································· 11分

答：略.··························································································· 12分

21．解：设参加夏令营活动的学生x人，每张车票的原价为a元，按第一种方案购票应付款y₁元，按第二种方案购票应付款y₂元，依题意得：······································································· 1分

y₁=5a+a×78%·x　 y₂=(x+5)·a·80%············································ 4分

（1）当y₂＞y₁时，（x+5）·a·80%　＞5a+a×78%·x 解得x＞50··· 5分

（2）当y₂=y₁时,（x+5）·a·80%=5a+a×78%·x  解得x=50·········· 6分

（3）当y₂＜y₁时，（x+5）·a·80%＜5a+a×78%x　解得x＜50········· 7分

答：当学生多于50人时，按第一种方案，当学生等于50人时，两种方案都可以，当学生少于50人时，按第二种方案.·············································································································· 8分

22．解：（1）猜想：AB⊥AC··························································· 1分

证明：分别连结O₁B、O₂C，··························································· 2分

则O₁B⊥BC　O₂C⊥BC，从而O₁B∥O₂C········································ 4分

∴∠BO₁O₂+∠CO₂O=180°····························································· 5分

∵∠ABC+∠ACB=∠BO₁O₂+∠CO₂O₁=90°····························· 6分

∴∠BAC=90°即AB⊥AC······························································· 7分

（2）亦有AB⊥AC，证明与（1）类似，略.···································· 8分

23．（1）A（-16，0） C（0，-12）················································· 2分

（2）过C作CB⊥AC，交x轴于点B，显然，点B为所求，··········· 3分

则OC²=OA×OB 此时OB=9，可求得B（9，0）····························· 5分

此时经过A，B，C三点的抛物线的解析式为：

y=x²+x-12·············································································· 8分

（3）当PQ∥BC时，△APQ ~△ACB·············································· 9分

得=·················································································· 10分

∴=解得m=··························································· 11分

当PQ⊥AB时，△APQ ~△ACB······················································ 12分

得：=··············································································· 13分

∴=　解得m=························································ 14分