中考模拟自测题
![]()
![]() 25.(本题满分12分)
25.(本题满分12分)
如图,二次函数![]() (m<4)的图象与
(m<4)的图象与![]() 轴相交于点A、B两点.
轴相交于点A、B两点.
(1)求点A、B的坐标(可用含字母![]() 的代数式表示);
的代数式表示);
(2)如果这个二次函数的图象与反比例函数![]() 的图象相交于点C,且
的图象相交于点C,且
∠BAC的余弦值为![]() ,求这个二次函数的解析式.
,求这个二次函数的解析式.

24.解:(1)当![]() ,
,![]() ,………………………………(1分)
,………………………………(1分)
![]() ,
,![]() .……………………………(2分)
.……………………………(2分)
∵![]() ,∴A(–4,0),B(
,∴A(–4,0),B(![]() ,0)………………………………(4分)
,0)………………………………(4分)
(2) 过点C作CD⊥![]() 轴,垂足为D,
轴,垂足为D,
cos∠BAC![]() ,设AD=4k,AC=5k, 则CD=3k. ……………………(5分)
,设AD=4k,AC=5k, 则CD=3k. ……………………(5分)
∵OA=4,∴OD=4k–4, 点C(4k–4,3k) . …………………………………(6分)
∵点C在反比例函数![]() 的图象上,∴
的图象上,∴![]() . ………………(7分)
. ………………(7分)
![]()
![]() . ……………………………(8分)
. ……………………………(8分)
∴C(2,![]() ).……………………(1分) ∵点C在二次函数的图象上,
).……………………(1分) ∵点C在二次函数的图象上,
∴![]() ,………(1分) ∴
,………(1分) ∴![]() ………………(10分)
………………(10分)
∴二次函数的解析式为![]() . ……………………………(12分)
. ……………………………(12分)
26.(本题满分14分)
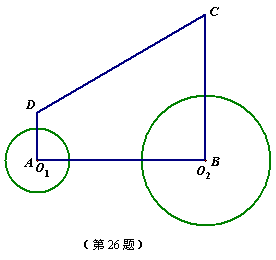
如图,直角梯形ABCD中,AD∥BC,∠A=90o,∠C=60°,AD=3cm,BC=9cm.⊙O1的圆心O1从点A开始沿折线A—D—C以1cm/s的速度向点C运动,⊙O2的圆心O2从点B开始沿BA边以![]() cm/s的速度向点A运动,⊙O1半径为2cm,⊙O2的半径为4cm,若O1、O2分别从点A、点B同时出发,运动的时间为ts
cm/s的速度向点A运动,⊙O1半径为2cm,⊙O2的半径为4cm,若O1、O2分别从点A、点B同时出发,运动的时间为ts
(1)请求出⊙O2与腰CD相切时t的值;
(2)在0s<t≤3s范围内,当t为何值时,⊙O1与⊙O2外切?
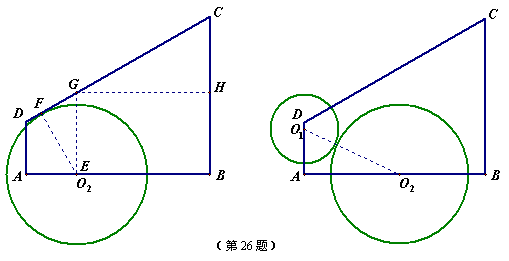
26.解:(1)如图所示,设点O2运动到点E处时,⊙O2与腰CD相切.
过点E作EF⊥DC,垂足为F,则EF=4cm.………………1分
方法一,作EG∥BC,交DC于G,作GH⊥BC,垂足为H.
通过解直角三角形,求得EB=GH=![]() cm.………………4分
cm.………………4分
所以t=(![]() )秒.………………6分
)秒.………………6分
方法二,延长EA、FD交于点P.通过相似三角形,也可求出EB长.
方法三,连结ED、EC,根据面积关系,列出含有t的方程,直接求t.
(2)由于0s<t≤3s,所以,点O1在边AD上.………………7分
如图所示,连结O1O2,则O1O2=6cm.………………8分
由勾股定理得,![]() ,即
,即![]() .………………10分
.………………10分
解得t1=3,t2=6(不合题意,舍去).………………12分
所以,经过3秒,⊙O1与⊙O2外切.………………14分
 |
25.(本题满分12分)
正方形ABCD的边长为4,P是BC上一动点,QP⊥AP交DC于Q,设PB=x,△ADQ的面积为y.
(1)求y与x之间的函数关系式,并写出自变量x的取值范围.
(2)(1)中函数若是一次函数,求出直线与两坐标轴围成的三角形面积,若是二次函数,请利用配方法求出抛物线的对称轴和顶点坐标.
(3)画出这个函数的图象.
(4)点P是否存在这样的位置,使△APB的面积是△ADQ的面积的![]() ,若存在,求出BP的长,若不存在,说明理由.
,若存在,求出BP的长,若不存在,说明理由.
25.解:(1)画出图形,设QC=z,由Rt△ABP~Rt△PCQ,
![]() =
=![]() ,
,
z=![]() ,①
,①
 y=
y=![]() ×4×(4-z),②
第25题图(1)
×4×(4-z),②
第25题图(1)
把①代入② y=![]() x2-2x+8(0<x<4).
x2-2x+8(0<x<4).
(2)y=![]() x2-2x+8=
x2-2x+8=![]() (x-2)2+6.
(x-2)2+6.
∴对称轴为x=2,顶点坐标为(2,6).
(3)如图所示 第25题图(2)
(4)存在,由S△APB=![]() S△ADQ,可得y=3x,
S△ADQ,可得y=3x,
∴![]() x2—2x+8=3x,
x2—2x+8=3x,
∴x=2,x=8(舍去),
∴当P为BC的中点时,△PAB的面积等于△ADQ的面积的![]() .
.
23.(14分)函数y=-![]() x-12的图象分别交x轴,y轴于A,C两点,
x-12的图象分别交x轴,y轴于A,C两点,
(1)求出A、C两点的坐标.
(2)在x轴上找出点B,使△ACB~△AOC,若抛物线经过A、B、C三点,求出抛物线的解析式.
(3)在(2)的条件下,设动点P、Q分别从A、B两点同时出发,以相同的速度沿AC、BA向C、A运动,连结PQ,设AP=m,是否存在m值,使以A、P、Q为顶点的三角形与△ABC相似,若存在,求出所有的m值;若不存在,请说明理由.
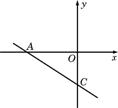
23.(1)A(-16,0) C(0,-12)················································· 2分
(2)过C作CB⊥AC,交x轴于点B,显然,点B为所求,············ 3分
则OC2=OA×OB 此时OB=9,可求得B(9,0)····························· 5分
此时经过A,B,C三点的抛物线的解析式为:
y=![]() x2+
x2+![]() x-12············································································· 8分
x-12············································································· 8分
(3)当PQ∥BC时,△APQ ~△ACB··············································· 9分
得![]() =
=![]() ·················································································· 10分
·················································································· 10分
∴![]() =
=![]() 解得m=
解得m=![]() ··························································· 11分
··························································· 11分
当PQ⊥AB时,△APQ ~△ACB······················································· 12分
得:![]() =
=![]() ··············································································· 13分
··············································································· 13分
∴![]() =
=![]() 解得m=
解得m=![]() ······················································· 14分
······················································· 14分

![]()
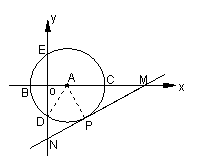
![]() 25.(本题满分10分)如图,在直角坐标系中,以点A(
25.(本题满分10分)如图,在直角坐标系中,以点A(![]() ,0)为圆心,以
,0)为圆心,以![]() 为半径的圆与x轴交于B、C两点,与y轴交于D、E两点.
为半径的圆与x轴交于B、C两点,与y轴交于D、E两点.
(1)求D点坐标.
(2)若B、C、D三点在抛物线![]() 上,求这个抛物线的解析式.
上,求这个抛物线的解析式.
(3)若⊙A的切线交x轴正半轴于点M,交y轴负半轴于点N,切点为P,∠OMN=30º,试判断直线MN是否经过所求抛物线的顶点?说明理由.
25.解:(1)连结AD,得OA=![]() ,AD=2
,AD=2![]() ……………………1分
……………………1分
∴OD=3, D(0,-3) ………………………………………………2分
(2)由B(-![]() ,0),C(3
,0),C(3![]() ,0),D(0,-3)三点在抛物线
,0),D(0,-3)三点在抛物线![]() 上,……3分
上,……3分
得
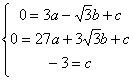 解得
解得 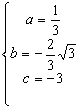 ………………………………5分
………………………………5分
∴![]() …………………………………………………………6分
…………………………………………………………6分
 (3)连结AP,在Rt△APM中,∠PMA==30º,AP=2
(3)连结AP,在Rt△APM中,∠PMA==30º,AP=2![]()
∴AM=4![]() , M (5
, M (5![]() ,0) …………………………7分
,0) …………………………7分
![]()
∴N(0,-5) ……………………………………………8分
直线MN解析式为:![]()
抛物线顶点坐标为(![]() ,-4) ………………………………9分
,-4) ………………………………9分
∵![]()
∴抛物线顶点在直线MN上. ……………………………10分
七、(12分)如图3.以A(0,![]() )为圆心的圆与x轴相切于坐标点O,与y轴相交于点B,弦BD的延长线交x轴的负半轴于点E, 且∠BEO = 600 , AD的延长线交x轴于点C.
)为圆心的圆与x轴相切于坐标点O,与y轴相交于点B,弦BD的延长线交x轴的负半轴于点E, 且∠BEO = 600 , AD的延长线交x轴于点C.
(1)分别求点E, C的坐标.
(2)求经过A、C两点,且以过E而平行于y轴的直线为对称轴的抛物线的函数解析式.
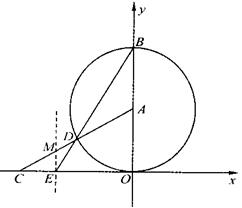 (3)设抛物线的对称轴与AC的交点为M,试判断以M点为圆心, ME为半径的圆与☉A的位置关系,并说明理由.
(3)设抛物线的对称轴与AC的交点为M,试判断以M点为圆心, ME为半径的圆与☉A的位置关系,并说明理由.
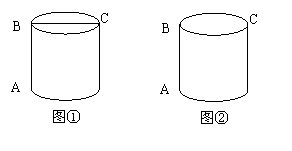
一个圆柱的一条母线为AB,BC是上底面的直径.一只蚂蚁从点A出发,沿着圆柱的表面爬行到点C.
⑴如图①,如果底面周长为24cm,高为4cm,那么蚂蚁的最短行程是多少cm?
⑵如图②,如果底面半径为rcm,高为hcm,那么你认为蚂蚁可能有哪几种行程较短的路径?试画出平面展开图说明路径(至少画两种不同的路径),不必说明理由.
⑶通过计算比较②中各种路径的长度,你能得到什么一般性的结论?或者说,蚂蚁选择哪条路径可使行程最短?
 |
28、(12分)某企业有员工300人,生产A种产品,平均每人每年可创造利润![]() 万元(
万元(![]() 为大于零的常数)。为减员增效,决定从中调配
为大于零的常数)。为减员增效,决定从中调配![]() 人去生产新开发的B种产品,根据评估,调配后,继续生产A种产品的员工平均每人每年创造的利润可增加20%,生产B种产品的员工平均每人每年可创造利润1.54
人去生产新开发的B种产品,根据评估,调配后,继续生产A种产品的员工平均每人每年创造的利润可增加20%,生产B种产品的员工平均每人每年可创造利润1.54![]() 万元。
万元。
(1)调配后,企业生产A种产品的年利润为_________万元,企业生产B种产品的年利润为_________万元(用含![]() 和
和![]() 的代数式表示)。若设调配后企业全年总利润为
的代数式表示)。若设调配后企业全年总利润为![]() 万元,则
万元,则![]() 与
与![]() 之间的关系式为
之间的关系式为![]() =____________。
=____________。
(2)若要求调配后,企业生产A种产品的年利润不小于调配前企业年利润的![]() ,生产B种产品的年利润大于调配前企业年利润的一半,应有哪几种调配方案
?请设计出来,并指出其中哪种方案全年总利润最大(必要时,运算过程可保留3个有效数字)。
,生产B种产品的年利润大于调配前企业年利润的一半,应有哪几种调配方案
?请设计出来,并指出其中哪种方案全年总利润最大(必要时,运算过程可保留3个有效数字)。
(3)企业决定将(2)中的年最大总利润(设![]() =2)继续投资开发新产品。现有6种产品可供选择(不得重复投资同一种产品)各产品所需资金及所获年利润如下表:
=2)继续投资开发新产品。现有6种产品可供选择(不得重复投资同一种产品)各产品所需资金及所获年利润如下表:
| 产 品 | C | D | E | F | G | H |
| 所需资金(万元) | 200 | 348 | 240 | 288 | 240 | 500 |
| 年 利 润(万元) | 50 | 80 | 20 | 60 | 40 | 85 |
如果你是企业决策者,为使此项投资所获年利润不少于145万元,你可以投资开发哪些产品?请写出两种投资方案。
28、解:(1)![]() ,
,![]() ,
,![]()
(2)由题意得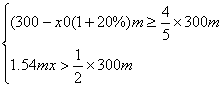
解得![]() <
<![]() ≤100。注:写97.5<
≤100。注:写97.5<![]() ≤100或97.4<
≤100或97.4<![]() ≤100均视为正确
≤100均视为正确
∵![]() 为整数 ∴
为整数 ∴![]() 只能取98、99、100。
只能取98、99、100。
故共有三种调配方案:
①202人继续生产A种产品,调98人生产B种产品;
②201人继续生产A种产品,调99人生产B种产品;
③200人继续生产A种产品,调100人生产B种产品;
又![]() =
=![]() ,由于
,由于![]() >0,函数
>0,函数![]() 随
随![]() 的增大而增大。故当
的增大而增大。故当![]() =100,即按第三种方案安排生产时,获总利润最大。
=100,即按第三种方案安排生产时,获总利润最大。
(3)当![]() =2时,最大总利润为788万元。根据题意,可投资开发产品F、H或C、D、E或C、D、G或C、F、G。
=2时,最大总利润为788万元。根据题意,可投资开发产品F、H或C、D、E或C、D、G或C、F、G。
30、已知:如图1,直线y=kx+3(k>0)交x轴于点B,交y轴于点A,以A点为圆心,AB为半径作⊙A交x轴于另一点D,交y轴于点E、F两点,交直线AB于C点,连结BE、CF,∠CBD的平分线交CE于点H.
(1)求证:BE=HE;
(2)若AH⊥CE,Q为 上一点,连结DQ交y轴于T,连结BQ并延长交y轴于G,
求AT•AG的值;
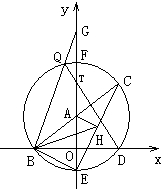 (3)如图2, P为线段AB上一动点(不与A、B两点重合),连结PD交y轴于点M,过P、M、B三点作⊙O1交y轴于另一点N,设⊙O1的半径为R,当k=时,给出下列两个结论:①MN的长度不变;②的值不变.其中有且只有一个结论是正确的,请你判断哪一个结论正确,证明正确的结论并求出其值.
(3)如图2, P为线段AB上一动点(不与A、B两点重合),连结PD交y轴于点M,过P、M、B三点作⊙O1交y轴于另一点N,设⊙O1的半径为R,当k=时,给出下列两个结论:①MN的长度不变;②的值不变.其中有且只有一个结论是正确的,请你判断哪一个结论正确,证明正确的结论并求出其值.

28、证明:(1)∵AE⊥BD,∴=,∴∠EBD=∠ECB.∵∠ABH=∠DBH,∠BHE=∠ECB+∠CBH,∠HBE=∠DBH+∠EBD,∴∠BHE=∠HBE. ∴BE=HE.
解: (2)连结QC、TB,则∠BCQ+∠CBQ=90°,又∠BDQ+∠ATD=90°,而∠BCQ=∠BDQ,∴∠CBQ=∠ATD=∠ATB,∴ΔABG∽ΔATB,∴AB2=AG•AT,∵AH⊥CE,∴H为CE的中点,∴BE=EC,∴ΔBEO∽ΔCBE,∴==. 设⊙A的半径为R,由AB2-OA2=BO2,OE=R-3,得R2-32=4(R-3)2,解得,R=5,或R=3(不合题意,舍去).∴AT•AG=AB2=25.
(方法二提示:可连结AD,CD证ΔBAG∽ΔTAD)
(3)答:②的值不变.
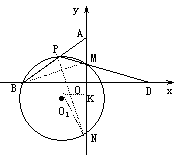 证明:作O1K⊥MN于K,连结O1N、PN、BM,
证明:作O1K⊥MN于K,连结O1N、PN、BM,
则MN=2NK, 且∠N O1K=∠NPM,
∴==2sin∠NO1K=2sin∠NPM,
由直线y=x+3 得 OB=OD=4,OM⊥BD,
∴∠BMO=∠DMO,
又∠BMO=∠ABM+∠BAM,∠DMO=∠MPN+∠PNM,
∵∠ABM=∠PNM,
∴∠MPN=∠BAM=∠NO1K,=2sin∠BAM=2×= ,
所以的值不变,其值为 .
23.(15分)已知抛物线![]() 与直线
与直线![]() :
:![]() 的交点除了原点
的交点除了原点![]() 外,还相交于另一点
外,还相交于另一点![]() .
.
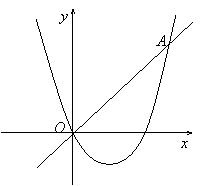 (1)分别求出这个抛物线的顶点、点
(1)分别求出这个抛物线的顶点、点![]() 的坐标(可用含
的坐标(可用含![]() 的式子表示);
的式子表示);
(2)将抛物线![]() 沿着
沿着![]() 轴对折(翻转
轴对折(翻转![]() )后,得到的图象叫做“新抛物线”,则:
)后,得到的图象叫做“新抛物线”,则:
①当![]() 时,求这个“新抛物线”的解析式,并判断这个“新抛物线”的顶点是否在直线
时,求这个“新抛物线”的解析式,并判断这个“新抛物线”的顶点是否在直线![]() 上;
上;
②在①的条件下,“新抛物线”上是否存在一点![]() ,使点
,使点![]() 到直线
到直线![]() 的距离等于线段
的距离等于线段![]() 的
的![]() ?若存在,请直接写出满足条件的点
?若存在,请直接写出满足条件的点![]() 坐标;若不存在,请说明理由。
坐标;若不存在,请说明理由。
28、(8分)如图:直线y=x-2与x轴、y轴分别交于点A、B,M(t,0)是x轴上异于A的一点,以M为圆心且过点A的圆记为⊙M.
(1)求证:直线AB将⊙M的周长分为1:3两部分;
(2)若直线AB被⊙M所截得的弦长为![]() ,求t的值;
,求t的值;
(3)若点N是⊙M上的一点,是否存在实数t,使得四边形ABMN为平行四边形?若存在,求出t的值,并写出N的坐标;若不存在,说明理由.


