中考试点班招生考试数学试卷

题　号	一	二	三	四	五	六	七	八	总　分
得　分

一、选择题：（每小题只有一个选项正确，请将正确选项的序号填入括号内，每小题3分，计30分）

1、下列各式正确的是　　　　　　　　　　　　　　　　　　　　　　　　　　 （　 ）

A、　　　　　　　 B、若

C、；D、若分式的值为正数，则

2、已知一次函数的图像如图1所示，当时，得取值范围是　　（　 ）

　　A、　　　　 B、　　　　 C、　　　　 D、

3、二次函数的图像如图2所示，下列结论正确的是　　　　　  （　 ）

　A、点在第四象限　　　　 B、抛物线的对称轴过第一、四象限C、反比例函数，当时，随的增大而减小；　D、化简：

4、已知　　　　　　　　　　　　　　　　 （　 ）

　A、6　　　　　　  B、　　　　　　　 C、　　　　　　　 D、

5、如图3，如果直线是多边形ABCDE的对称轴，其中的度数是： A、　　　 B、　　  C、　　　 D、70　　　　　  （　 ）

6、如图4在矩形ABCD中,为（　 ）

　A、3　　　　　　  B、　　　　　　　 C、　　　　　　  D、

7、几位同学拍了一张合影作留念，已知冲一张底片需要0.80元，洗一张相片需要0.35元，在每位同学得到一张相片且共用一张底片的前提下，平均每人分摊的钱不足0.50元，那么参加合影的同学人数为　　　　　　　　　　　　　　　　　　　　　　　  （　 ）

A、至多6人　　　　B、至少6人　　　　  C、至多5人　　　　  D、至少5人

8、2002年8月在北京召开的国际数学家大会徽标如图5所示，它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形。若大正方形面积为13，小正方形面积为1，直角三角形的较长直角边为，较短直角边为，则的值为　　　　　　　　　　  （　 ）

 A、97　　　　　　  B、89　　　　　　　  C、43　　　　　　　  D、35

9、若等腰三角形一腰上的高等于腰长的一半，则此三角形的底角等于　　　　　　  （　 ）

 A、　　　　　  B、　　　　　　  C、　　　　　　 D、

10、如图6，在矩形ABCD中，对角线AC、BD相交于点G，E为AD的中点。连接BE

交AC于点F，连接FD。若：⑴ △与△

⑵△与△ ⑶ △与△ ⑷ △与△，其中相似的有　 （　 ）

　A、⑴ ⑷　　　　 B、⑴ ⑵　　　　　  C、⑵ ⑶ ⑷　　　　　 D、⑴ ⑵ ⑶

二、填空题：（每题3分，计18分）

11、若不等式组的解集是，则

12、若

13、如图7在△中AB=AC, M、N分别是的中点，D、E为BC上的点，连

接若AB=13

14、如图8已知在⊙O中，直径MN=10，正方形ABCD的四个顶点分别在半径OM、OP

以及⊙O上，且

15、如图9矩形AOCB的两边分别位于轴，轴上。点B的坐标为，

D是AB边上一点，将△沿直线OD翻折使A点恰好落在对角线OB上的点E处。

若点E在一反比例函数的图像上，那么该函数的解析式为 ___________

16、如图10，在△中AC=CB=2，

点，则EC+ED的最小值是 ______

三、先化简，再求值（本题满分5分）

17、

四、（本题满分6分）

18、如图□ABCD中，E为BC边上一点，且AB=AE.

⑴ 求证：△≌△

⑵ 若AE平分

五、（本题满分9分）

19、如果一个正整数能表示为两个连续偶数的平方差，那么称这个正整数为“神秘数”，如

⑴ 28和2012这两个数是“神秘数”吗？为什么？

⑵ 设两个连续偶数为和，由这两个连续偶数构成的“神秘数”是4的倍数吗？为什么？

⑶ 两个连续奇数的平方差（取正数）是“神秘数”吗？为什么？

六、（本题满分10分）

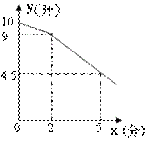
20、课间休息时，同学们到饮水机旁依次每人接水0.25升，他们先打开了一个饮水管，

后来又打开了第二个饮水管。假设接水的过程中每根饮水管出水的速度是匀速的，在

不关闭饮水管的情况下，饮水机水桶内的存水量的函数关系图

像如图所示。请结合图像回答下列问题：

⑴　　存水量的函数关系式；

⑵　　如果接水的同学有28名，那么他们都接完水需要几分钟？

⑶　　如果有若干名同学按上述方法接水，他们接水所用时间要比只开第一个饮水管接水的时间少用2分钟，那么有多少名学生接完水？

七、（本题满分10分）

21、嘉年华游乐场投资150万元引导一项大型游乐设施。若不计维修保养费用，预计开放后每月可创收33万元。而该游乐设施开放后，从第一个月到第个月的维修费用累计为且；若将创收扣除投资和维修保养费用后的称为纯收益，也是关于的二次函数。

⑴ 若维修保养费用第一个月为2万元，第二个月为4万元。求关于的解析式

⑵ 求纯收益关于的解析式

⑶ 问：设施开放几个月后，游乐场的纯收益达到最大？几个月后能收回投资？

八、（本题满分12分）

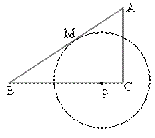
22、如图Rt△的两条直角边, 点P是边BC上的一动点（P不与B重合）

以P为圆心作⊙P与BA相切于点M。设,⊙P的半径为

⑴　　求证：△∽△

⑵　　求与的函数关系式，并确定当在什么范围内取值时，⊙P与AC所在直线相离？

⑶　　当点P从点C向点B移动时，是否存在这样的⊙P，使得它与△的外接圆相内切？若存在，求出的值；若不存在，请说明理由。