九年级第二学期数学试卷
（满分150分，考试时间100分钟）
| 题号 | 一 | 二 | 三 | 四 | 总分 | |||||||
| 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | ||||
| 得分 | ||||||||||||
考生注意：
1．本卷含四大题，共25题；
2．除第一、二大题外，其余各题如无特别说明，都必须写出证明或计算的主要步骤．
一．填空题：（本大题共12题，满分36分）
【只要求直接写出结果，每个空格填对得3分，否则得零分】
1.
计算：
=______________．
2.
如果分式
的值为零，那么x的值为_______．
3.
计算：
＝____________．
4.
不等式组
的解集是__________________．
5.
如果方程
有两个实数根，那么
的取值范围是___________.
6.
函数y =
的定义域是_____________．
7. 写出一个图象不经过第三象限的一次函数：______________．
8.
二次函数
的顶点坐标是_________.
9.
在⊙O中，AB是直径，弦AC的弦心距为3，那么BC的长为_________.
10.
已知正方形桌子桌面边长为80
，要买一块正方形桌布，如图铺设时，四周垂下的桌布都是等腰直角三角形，且桌面四个角的顶点恰好在桌布边上，那么要买桌布的边长是
cm（精确到个位，备用数据：
）.
11.
在△ABC中,点D、E分别在边AB、AC上，要使△ADE与△ABC相似, 只须添加一个条件, 这个条件可以是_____________
(只要填写一种情况).
12.
如图,在Rt△ABC中, ∠C=90º,∠B=30º, 将△ABC绕着点C逆时针旋转后得到的△A′B′C的斜边A′B′ 经过点A, 那么旋转角的度数是______________.
二．选择题：（本大题共4题，满分16分）
【下列各题的四个结论中，有且只有一个结论是正确的，把正确结论的代号写在题后的圆括号内，选对得4分；不选、错选或者多选得零分】
13.
如果
，那么下列各式中一定正确的是………………………………（ ）
（A） 
； （B）
； （C）
； （D）
．
14.
一元二次方程
两根的和为 ………………………………（ ）
（A）
； （B）
； （C）–2； （D）2．
15.
如果一个斜坡的长度为
米，坡角为
，那么斜坡的高度是……………（ ）
（A）
； （B）
； （C）
； （D）
.
16. 如果两圆的两条公切线互相垂直，那么这两个圆的位置关系不可能为…（ ）
（A）外离； （B）相交； （C）外切； （D）内切．
三．（本大题共5题，满分48分）
17. （本题满分9分）
先化简，再求值：
，其中
．
18. （本题满分9分）
解方程：
．
19. （本题满分10分，每小题满分各5分）
小明申请使用了某电信公司的手机来电畅听业务，这个公司的来电畅听业务规定：用户每月交月租费16元，可免费接听来电，而打出电话每分钟收费0.13元．
(1)
写出小明一个月手机的通话费(包括月租费和打出电话)
(元)与打出电话时间
(分钟)的解析式，并写出函数定义域.
(2) 如果小明某个月手机的通话费(包括月租费和打出电话)为42元,试求小明该月打出电话的时间.
20. (本题满分10分,第(1)、(2)每小题满分各3分,第(3)、(4)每小题满分各2分)
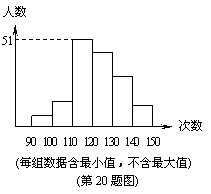某校九年级部分学生举行了一次一分钟跳绳测试，将测试成绩整理后作出如下统计图．已知从左到右前四组的频率依次为0.04、0.08、0.34、0.3，结合统计图所提供的的信息回答下列问题：
（1）这次参加测试的学生共________人.
（2）跳绳次数少于100次的学生有_______人.（3）如果跳绳次数不少于130次为优秀，那么
这次测试成绩的优秀率是__________.
（4）如果这次测试成绩的中位数是120次，那
么这次测试中，成绩为120次的学生至少
有_________人.
21. （本题满分10分，每小题满分各5分）
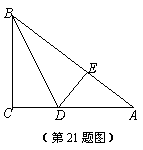如图，在△ABC中，∠C=90°, 点D、E分别在边AC、AB上，BD平分∠ABC，DE⊥AB, AE=8，cosA=
．
(1) 求CD的长；
(2) 求tg∠DBC的值．
五、（本大题共4题，满分50分）
22. （本题满分12分）
已知：如图，在四边形ABCD中, AD//BC, AC⊥BC，点E、F分别是边AB、CD的中点，AF = CE．
求证：AD=BC．
|
23. （本题满分12分，每小题满分各6分）
如图，反比例函数的图象与二次函数
的图象在第一象限内相交于A、B两点，A、B两点的纵坐标分别为1、3，且AB=
．
（１） 求反比例函数的解析式；
（２） 求二次函数的解析式．
24. （本题满分12分）
如图，路灯A的高度为7米，在距离路灯正下方B点20米处有一墙壁CD，CD⊥BD，如果身高为1.6米的学生EF站立在线段BD上（EF⊥BD，垂足为F，EF<CD），他的影子的总长度为3米, 求该学生到路灯正下方B点的距离BF的长.
25．(本题满分14分,第(1)小题满分4分,第(2)小题满分6分,第(3)小题满分4分)
如图，线段AB=1，点C在线段AB上，以AC为半径的⊙A与以CB为半径的⊙C相交于点D，BD的延长线与⊙A相交于点E，CD、AE的延长线相交于点F．
（1）
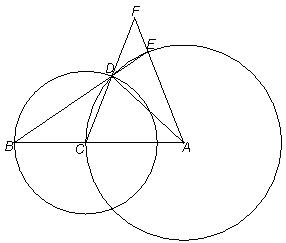求证：∠ADB=3∠B；
（2） 设⊙C的半径为
，EF的长为，求与的函数解析式，并写出定义域；
（3） 点C在线段AB上移动的过程中，⊙C能否与AE相切？如果能够，请求出这时⊙C的半径；如果不能，请说明理由．
|