九年级数学第二学期第一次质量调查　　　　 姓名　　　　　　 

一，选择题：

1．  已知为锐角， tan(90⁰－)=,则的度数为（　　）

A;30⁰　　　　  B;45⁰　　　　 C;60⁰　　　　  D;75⁰

2.化简的结果是（　  ）

A;　　　 B;　　  C;　　　 D;a≠b

3.为了了解一批数据在各小范围内所占比例大小，将这批数据分组，落在各小组内的数据个数叫（）

A;频率　B;样本容量　C;频数　D;频数累计

4．下列图中，①正方形　②圆　③等腰梯形　④平行四边形，是轴对称图形，但不是中心对称图形的有（　　）

A;1个　　　　　  B;2个　　　　　  C;3个　　　　　　  D;4个

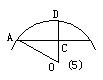
5．圆弧形蔬菜大棚的剖面如图所示，AB=8cm,∠CAD=30⁰,则大棚高度CD约为（　　）

A;2.0m　　　　　 B;2.3m　　　　　  C;4.6m　　　　　　 D;6.9m

  

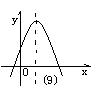
6．梯形ABCD中，AB∥CD,E,F,G,H分别是梯形ABCD各边AB,BC,CD,DA的中点，要使四边形EFGH是菱形，下列补充的条件不正确的是（　　）

A;AC=BD　　　　B;AC⊥BD　　　　  C;AD=BC　　　　 D;∠D=∠C

7.如图，在四边形ABCD中，F是AD延长线上一点，连结BF交DC于点E，则图中的相似三角形共有（　　）

A;0对　　　　　  B;1对　　　　　　  C;2对　　　　　 D;3对

8.已知关于x的方程，有两个不相等的实数根，那么使该方程的两个实数根互为相反数的k的值是（　）

A;不存在;　　　　  B;1　　　　　　　  C;－1　　　　　 D;

9.二次函数y=ax²+bx+c的图像如图,则点(b, ) 在（　 ）

A;第一象限　　　　 B；第二象限　　　　C;第三象限　　 D;第四象限

10.给出下列四个命题

①如果某圆锥的侧面展开图是半圆，则其轴截面一定是等边三角形。

②如果点A在直线y=2x－3上，且点A到两坐标轴的距离相等，则点A在第一或第四象限。

③在半径为5的圆中，弦AB=8,则圆周上到直线AB的距离为2的点共有4个。

④若A(a, m),B(a－1,n)在反比例函数的图像上，则m<n.

其中正确的命题的个数是（　　）

A;1个　　　　　  B;2个　　　　　　　 C;3个　　　　　  D;4个

二，填空题：

11．不等式组 x－2<1 的解集是（　　　）

2x+1>5

12.计算所得的结果是（　　）

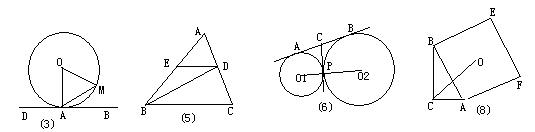
13．如图，DB切⊙O于A,∠AOM=66⁰,则∠DAM=(　　　)度。

14．一组数据：4, 0, 1, －2, 2的标准差是(　　 )

15.已知如图，△ABC中，BD平分∠ABC，且D为AC的中点，DE∥BC交AB于点E，若BC=4，则EB长为(　　 ).

16.如图，⊙O₁和⊙O₂外切于点P，内公切线PC与外公切线AB(A,B分别是⊙O₁和⊙O₂上的切点)相交于点C，已知⊙O₁和⊙O₂的半径分别为3和4，则PC的长为（　　 ）

17.一次函数的图像过点（1，2），且y随x的增大而增大，则这个一次函数解析式是（　　　　）.

18.如图，在Rt△ABC中，∠C=90⁰,AC=3 ,BC=5,以AB为边向外作正方形ABEF，则正方形中心O与点C的连线的长等于（　　 ）

三，解答题：

19．解方程：　

20．已知抛物线y=(1－m)x²+4x－3开口向下，与x轴交于A(x₁ ,0 )和B(x₂ , 0 )两点。其中x₁<x₂，

（1）　　　 求m的取值范围

（2）　　　 若,求抛物线的解析式。

21.如图，Rt△ABO的顶点A是双曲线y=与直线y=－x－(k+1)在第二象限的交点，AB⊥x轴于B，且S_△ABO=

(1)　  求这两个函数的解析式。

(2)　  求直线与双曲线的两个交点A,C的坐标

22.已知，如图，四边形ABCD内接于⊙O，过点A的切线与CD的延长线交于E，且∠ADE=∠BDC

（1）　　　 求证：△ABC为等腰三角形。

（2）　　　 若AE=6 , BC=12 ,CD=5 ,求AD的长。

23.如图，甲，乙为住宅区内的两栋楼，它们的高AB=CD=30m, 两楼间的距离AC=14m，现在需要了解甲楼对乙楼的采光的影响情况，当太阳光与水平线的夹角为30⁰时，求甲楼的影子在乙楼上有多高？

（精确到0.1m, ）

24.某市电讯局现有300部已申请装机的电话等待装机，此外每天还有若干部新申请的电话等待装机。假设每天申请装机的电话部数相同，该电讯局每个电话装机小组每天装的电话部数也相等，那么安排3个装机小组，恰好30天可将等待装机的电话装完；如果安排5个装机小组，则恰好在10天可将等待装机的电话装完，试求每天有多少部新申请装机的电话。

25．如图所示，在△ABC中，点O是AC边上的一个动点，过点O作直线MN∥BC,，设MN交∠BCA的平分线于E，交∠BCA的外角平分线于F

(1)　  求证：EO=FO

(2)　  当点O运动到何处时，四边形AECF是矩形？并证明你的结论。

(3)　  若AC边上存在点O，使四边形AECF是正方形，且，求∠B的大小.

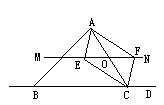
26．已知抛物线y=ax²+bx+c经过A(－1, 2 ),B(2 ,－1 )两点，且于y轴交于点M。

（1）　　　 求:b和c（用含a的代数式表示）

（2）　　　 求抛物线y=ax²－bx+c－1上横坐标与纵坐标相等的点的坐标。

（3）　　　 在第（2）小题所求出的点中，有一个也在抛物线y=ax²+bx+c上，试判断直线AM和x轴的位置关系，并说明理由。

参考答案：

选择题：1。A　2。A　3。C　4。A　 5。B　6。B　7。D　8。A　9。D　10。B

11.2<x<3　　12. 2a　 13.147　　 14.2　　  15.2　　 16.2　  17.y=x+1,y=2x, y=3x－1等　18.4　　 19.x₁=－2, x₂=1　  20.1<m< ,y=－x²+4x－3　　  21.y=－ ,y=－x+2; A(－1,3)B(3,－1)

22.AD=8　　 23.16.2m　　　　 24.每天有20部新申请装机的电话　 25。（1）略 （2）O为AC中点(3)∠B=60⁰　　　 26.(1)b=－a－1, c=1－2a　　(2)(1,1)或（－2，－2） （3）当P₁(1,1)在抛物线C₁上时，直线AM平行于轴x，；当P₂(－2, －2)在抛物线C₁上时，直线AM与x轴相交。